Divergence Theorem on:
[Wikipedia]
[Google]
[Amazon]
In
 Suppose is a
Suppose is a
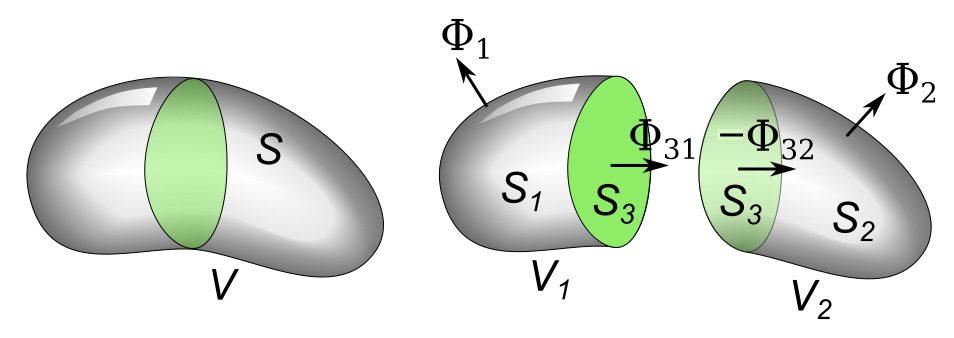 See the diagram. A closed, bounded volume is divided into two volumes and by a surface ''(green)''. The flux out of each component region is equal to the sum of the flux through its two faces, so the sum of the flux out of the two parts is
:
where and are the flux out of surfaces and , is the flux through out of volume 1, and is the flux through out of volume 2. The point is that surface is part of the surface of both volumes. The "outward" direction of the normal vector is opposite for each volume, so the flux out of one through is equal to the negative of the flux out of the other so these two fluxes cancel in the sum.
:
Therefore:
:
Since the union of surfaces and is
:
See the diagram. A closed, bounded volume is divided into two volumes and by a surface ''(green)''. The flux out of each component region is equal to the sum of the flux through its two faces, so the sum of the flux out of the two parts is
:
where and are the flux out of surfaces and , is the flux through out of volume 1, and is the flux through out of volume 2. The point is that surface is part of the surface of both volumes. The "outward" direction of the normal vector is opposite for each volume, so the flux out of one through is equal to the negative of the flux out of the other so these two fluxes cancel in the sum.
:
Therefore:
:
Since the union of surfaces and is
:
 This principle applies to a volume divided into any number of parts, as shown in the diagram. Since the integral over each internal partition ''(green surfaces)'' appears with opposite signs in the flux of the two adjacent volumes they cancel out, and the only contribution to the flux is the integral over the external surfaces ''(grey)''. Since the external surfaces of all the component volumes equal the original surface.
:
This principle applies to a volume divided into any number of parts, as shown in the diagram. Since the integral over each internal partition ''(green surfaces)'' appears with opposite signs in the flux of the two adjacent volumes they cancel out, and the only contribution to the flux is the integral over the external surfaces ''(grey)''. Since the external surfaces of all the component volumes equal the original surface.
:
 The flux out of each volume is the surface integral of the vector field over the surface
:
The goal is to divide the original volume into infinitely many infinitesimal volumes. As the volume is divided into smaller and smaller parts, the surface integral on the right, the flux out of each subvolume, approaches zero because the surface area approaches zero. However, from the definition of
The flux out of each volume is the surface integral of the vector field over the surface
:
The goal is to divide the original volume into infinitely many infinitesimal volumes. As the volume is divided into smaller and smaller parts, the surface integral on the right, the flux out of each subvolume, approaches zero because the surface area approaches zero. However, from the definition of
/ref> :: :The last term on the right vanishes for constant or any divergence free (solenoidal) vector field, e.g. Incompressible flows without sources or sinks such as phase change or chemical reactions etc. In particular, taking to be constant: :: * With for vector field and constant vector c: :: : By reordering the
 Suppose we wish to evaluate
:
where is the
Suppose we wish to evaluate
:
where is the
vector calculus
Vector calculus or vector analysis is a branch of mathematics concerned with the differentiation and integration of vector fields, primarily in three-dimensional Euclidean space, \mathbb^3. The term ''vector calculus'' is sometimes used as a ...
, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem
In mathematics and formal logic, a theorem is a statement (logic), statement that has been Mathematical proof, proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to esta ...
relating the '' flux'' of a vector field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and dire ...
through a closed surface to the ''divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
'' of the field in the volume enclosed.
More precisely, the divergence theorem states that the surface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, o ...
of a vector field over a closed surface, which is called the "flux" through the surface, is equal to the volume integral of the divergence over the region enclosed by the surface. Intuitively, it states that "the sum of all sources of the field in a region (with sinks regarded as negative sources) gives the net flux out of the region".
The divergence theorem is an important result for the mathematics of physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
and engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
, particularly in electrostatics
Electrostatics is a branch of physics that studies slow-moving or stationary electric charges.
Since classical antiquity, classical times, it has been known that some materials, such as amber, attract lightweight particles after triboelectric e ...
and fluid dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion ...
. In these fields, it is usually applied in three dimensions. However, it generalizes to any number of dimensions. In one dimension, it is equivalent to the fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of derivative, differentiating a function (mathematics), function (calculating its slopes, or rate of change at every point on its domain) with the concept of integral, inte ...
. In two dimensions, it is equivalent to Green's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region (surface in \R^2) bounded by . It is the two-dimensional special case of Stokes' theorem (surface in \R^3) ...
.
Explanation using liquid flow
Vector field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and dire ...
s are often illustrated using the example of the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
field of a fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
, such as a gas or liquid. A moving liquid has a velocity—a speed and a direction—at each point, which can be represented by a vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
, so that the velocity of the liquid at any moment forms a vector field. Consider an imaginary closed surface ''S'' inside a body of liquid, enclosing a volume of liquid. The flux of liquid out of the volume at any time is equal to the volume rate of fluid crossing this surface, i.e., the surface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, o ...
of the velocity over the surface.
Since liquids are incompressible, the amount of liquid inside a closed volume is constant; if there are no sources or sinks inside the volume then the flux of liquid out of ''S'' is zero. If the liquid is moving, it may flow into the volume at some points on the surface ''S'' and out of the volume at other points, but the amounts flowing in and out at any moment are equal, so the ''net'' flux of liquid out of the volume is zero.
However, if a ''source'' of liquid is inside the closed surface, such as a pipe through which liquid is introduced, the additional liquid will exert pressure on the surrounding liquid, causing an outward flow in all directions. This will cause a net outward flow through the surface ''S''. The flux outward through ''S'' equals the volume rate of flow of fluid into ''S'' from the pipe. Similarly if there is a ''sink'' or drain inside ''S'', such as a pipe which drains the liquid off, the external pressure of the liquid will cause a velocity throughout the liquid directed inward toward the location of the drain. The volume rate of flow of liquid inward through the surface ''S'' equals the rate of liquid removed by the sink.
If there are multiple sources and sinks of liquid inside ''S'', the flux through the surface can be calculated by adding up the volume rate of liquid added by the sources and subtracting the rate of liquid drained off by the sinks. The volume rate of flow of liquid through a source or sink (with the flow through a sink given a negative sign) is equal to the ''divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
'' of the velocity field at the pipe mouth, so adding up (integrating) the divergence of the liquid throughout the volume enclosed by ''S'' equals the volume rate of flux through ''S''. This is the divergence theorem.
The divergence theorem is employed in any conservation law which states that the total volume of all sinks and sources, that is the volume integral of the divergence, is equal to the net flow across the volume's boundary.
Mathematical statement
subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they a ...
of (in the case of represents a volume in three-dimensional space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three- ...
) which is compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
and has a piecewise
In mathematics, a piecewise function (also called a piecewise-defined function, a hybrid function, or a function defined by cases) is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be ...
smooth boundary (also indicated with ). If is a continuously differentiable vector field defined on a neighborhood
A neighbourhood (Commonwealth English) or neighborhood (American English) is a geographically localized community within a larger town, city, suburb or rural area, sometimes consisting of a single street and the buildings lining it. Neigh ...
of , then:
:
The left side is a volume integral over the volume , and the right side is the surface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, o ...
over the boundary of the volume . The closed, measurable set is oriented by outward-pointing normals, and is the outward pointing unit normal at almost each point on the boundary . ( may be used as a shorthand for .) In terms of the intuitive description above, the left-hand side of the equation represents the total of the sources in the volume , and the right-hand side represents the total flow across the boundary .
Informal derivation
The divergence theorem follows from the fact that if a volume is partitioned into separate parts, the flux out of the original volume is equal to the algebraic sum of the flux out of each component volume. This is true despite the fact that the new subvolumes have surfaces that were not part of the original volume's surface, because these surfaces are just partitions between two of the subvolumes and the flux through them just passes from one volume to the other and so cancels out when the flux out of the subvolumes is summed. See the diagram. A closed, bounded volume is divided into two volumes and by a surface ''(green)''. The flux out of each component region is equal to the sum of the flux through its two faces, so the sum of the flux out of the two parts is
:
where and are the flux out of surfaces and , is the flux through out of volume 1, and is the flux through out of volume 2. The point is that surface is part of the surface of both volumes. The "outward" direction of the normal vector is opposite for each volume, so the flux out of one through is equal to the negative of the flux out of the other so these two fluxes cancel in the sum.
:
Therefore:
:
Since the union of surfaces and is
:
See the diagram. A closed, bounded volume is divided into two volumes and by a surface ''(green)''. The flux out of each component region is equal to the sum of the flux through its two faces, so the sum of the flux out of the two parts is
:
where and are the flux out of surfaces and , is the flux through out of volume 1, and is the flux through out of volume 2. The point is that surface is part of the surface of both volumes. The "outward" direction of the normal vector is opposite for each volume, so the flux out of one through is equal to the negative of the flux out of the other so these two fluxes cancel in the sum.
:
Therefore:
:
Since the union of surfaces and is
:
 This principle applies to a volume divided into any number of parts, as shown in the diagram. Since the integral over each internal partition ''(green surfaces)'' appears with opposite signs in the flux of the two adjacent volumes they cancel out, and the only contribution to the flux is the integral over the external surfaces ''(grey)''. Since the external surfaces of all the component volumes equal the original surface.
:
This principle applies to a volume divided into any number of parts, as shown in the diagram. Since the integral over each internal partition ''(green surfaces)'' appears with opposite signs in the flux of the two adjacent volumes they cancel out, and the only contribution to the flux is the integral over the external surfaces ''(grey)''. Since the external surfaces of all the component volumes equal the original surface.
:
 The flux out of each volume is the surface integral of the vector field over the surface
:
The goal is to divide the original volume into infinitely many infinitesimal volumes. As the volume is divided into smaller and smaller parts, the surface integral on the right, the flux out of each subvolume, approaches zero because the surface area approaches zero. However, from the definition of
The flux out of each volume is the surface integral of the vector field over the surface
:
The goal is to divide the original volume into infinitely many infinitesimal volumes. As the volume is divided into smaller and smaller parts, the surface integral on the right, the flux out of each subvolume, approaches zero because the surface area approaches zero. However, from the definition of divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
, the ratio of flux to volume, , the part in parentheses below, does not in general vanish but approaches the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
as the volume approaches zero.
:
As long as the vector field has continuous derivatives, the sum above holds even in the limit when the volume is divided into infinitely small increments
:
As approaches zero volume, it becomes the infinitesimal , the part in parentheses becomes the divergence, and the sum becomes a volume integral over
Since this derivation is coordinate free, it shows that the divergence does not depend on the coordinates used.
Proofs
For bounded open subsets of Euclidean space
We are going to prove the following: Proof of Theorem.For compact Riemannian manifolds with boundary
We are going to prove the following: Proof of Theorem. We use the Einstein summation convention. By using a partition of unity, we may assume that and have compact support in a coordinate patch . First consider the case where the patch is disjoint from . Then is identified with an open subset of and integration by parts produces no boundary terms: In the last equality we used the Voss-Weyl coordinate formula for the divergence, although the preceding identity could be used to define as the formal adjoint of . Now suppose intersects . Then is identified with an open set in . We zero extend and to and perform integration by parts to obtain where . By a variant of the straightening theorem for vector fields, we may choose so that is the inward unit normal at . In this case is the volume element on and the above formula reads This completes the proof.Corollaries
By replacing in the divergence theorem with specific forms, other useful identities can be derived (cf. vector identities). * With for a scalar function and a vector field , :: :A special case of this is , in which case the theorem is the basis for Green's identities. * With for two vector fields and , where denotes a cross product, :: * With for two vector fields and , where denotes adot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
,
::
* With for a scalar function and vector field c:MathWorld/ref> :: :The last term on the right vanishes for constant or any divergence free (solenoidal) vector field, e.g. Incompressible flows without sources or sinks such as phase change or chemical reactions etc. In particular, taking to be constant: :: * With for vector field and constant vector c: :: : By reordering the
triple product
In geometry and algebra, the triple product is a product of three 3- dimensional vectors, usually Euclidean vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the ve ...
on the right hand side and taking out the constant vector of the integral,
::
: Hence,
::
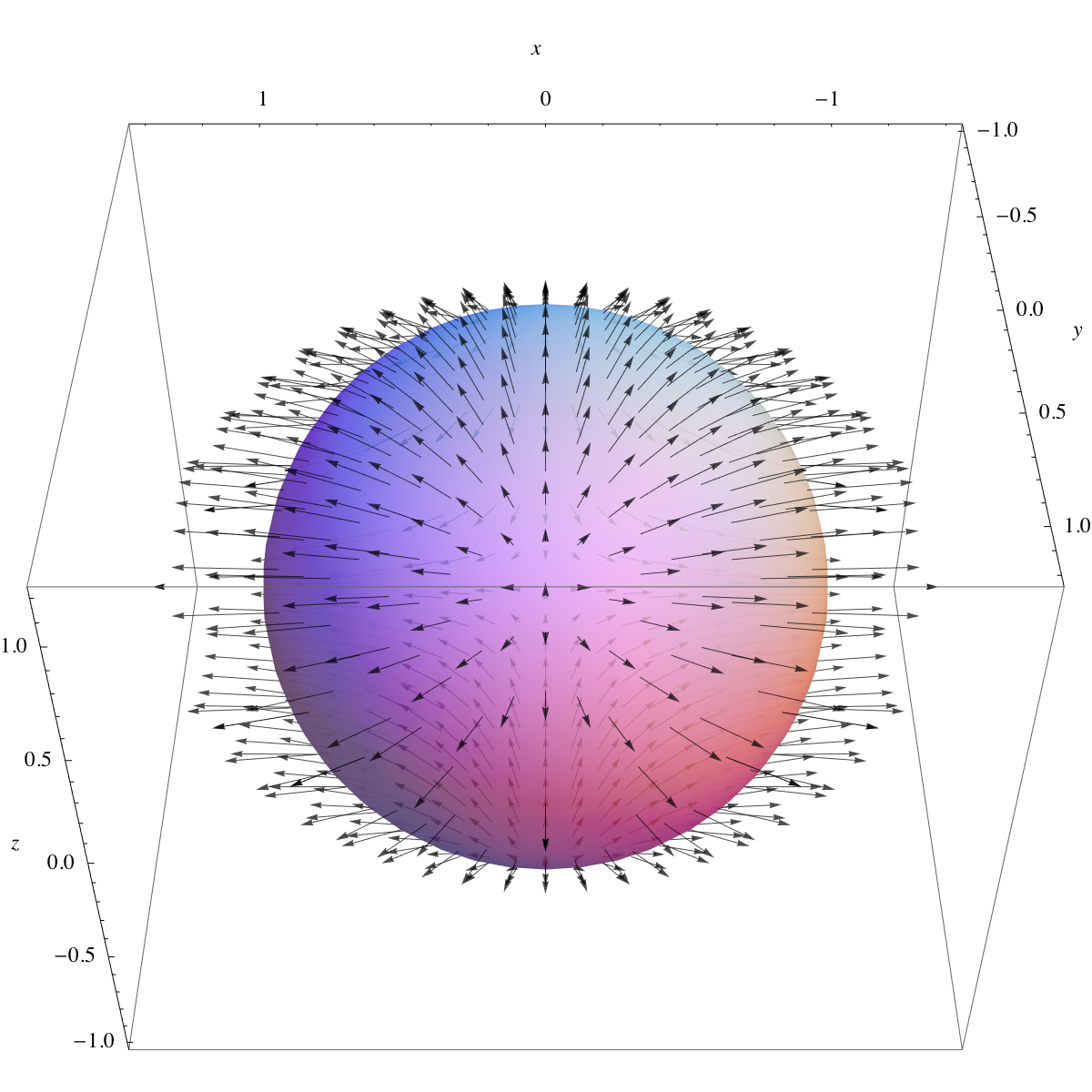
Example

unit sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -s ...
defined by
:
and is the vector field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and dire ...
:
The direct computation of this integral is quite difficult, but we can simplify the derivation of the result using the divergence theorem, because the divergence theorem says that the integral is equal to:
:
where is the unit ball
Unit may refer to:
General measurement
* Unit of measurement, a definite magnitude of a physical quantity, defined and adopted by convention or by law
**International System of Units (SI), modern form of the metric system
**English units, histo ...
:
:
Since the function is positive in one hemisphere of and negative in the other, in an equal and opposite way, its total integral over is zero. The same is true for :
:
Therefore,
:
because the unit ball has volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
.
Applications
Differential and integral forms of physical laws
As a result of the divergence theorem, a host of physical laws can be written in both a differential form (where one quantity is the divergence of another) and an integral form (where the flux of one quantity through a closed surface is equal to another quantity). Three examples are Gauss's law (inelectrostatics
Electrostatics is a branch of physics that studies slow-moving or stationary electric charges.
Since classical antiquity, classical times, it has been known that some materials, such as amber, attract lightweight particles after triboelectric e ...
), Gauss's law for magnetism, and Gauss's law for gravity.
Continuity equations
Continuity equations offer more examples of laws with both differential and integral forms, related to each other by the divergence theorem. Influid dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion ...
, electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interacti ...
, quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, relativity theory, and a number of other fields, there are continuity equations that describe the conservation of mass, momentum, energy, probability, or other quantities. Generically, these equations state that the divergence of the flow of the conserved quantity is equal to the distribution of ''sources'' or ''sinks'' of that quantity. The divergence theorem states that any such continuity equation can be written in a differential form (in terms of a divergence) and an integral form (in terms of a flux).
Inverse-square laws
Any '' inverse-square law'' can instead be written in a ''Gauss's law''-type form (with a differential and integral form, as described above). Two examples are Gauss's law (in electrostatics), which follows from the inverse-squareCoulomb's law
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental scientific law, law of physics that calculates the amount of force (physics), force between two electric charge, electrically charged particles at rest. This electric for ...
, and Gauss's law for gravity, which follows from the inverse-square Newton's law of universal gravitation
Newton's law of universal gravitation describes gravity as a force by stating that every particle attracts every other particle in the universe with a force that is Proportionality (mathematics)#Direct proportionality, proportional to the product ...
. The derivation of the Gauss's law-type equation from the inverse-square formulation or vice versa is exactly the same in both cases; see either of those articles for details.
History
Joseph-Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaMécanique Analytique.'' Lagrange employed surface integrals in his work on fluid mechanics. He discovered the divergence theorem in 1762.
, and
).
Differential Operators and the Divergence Theorem
at MathPages
The Divergence (Gauss) Theorem
by Nick Bykov,
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
was also using surface integrals while working on the gravitational attraction of an elliptical spheroid in 1813, when he proved special cases of the divergence theorem. He proved additional special cases in 1833 and 1839. But it was Mikhail Ostrogradsky, who gave the first proof of the general theorem, in 1826, as part of his investigation of heat flow. Special cases were proven by George Green in 1828 in ''An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism'', Siméon Denis Poisson
Baron Siméon Denis Poisson (, ; ; 21 June 1781 – 25 April 1840) was a French mathematician and physicist who worked on statistics, complex analysis, partial differential equations, the calculus of variations, analytical mechanics, electricity ...
in 1824 in a paper on elasticity, and Frédéric Sarrus in 1828 in his work on floating bodies.
Worked examples
Example 1
To verify the planar variant of the divergence theorem for a region : : and the vector field: : The boundary of is the unit circle, , that can be represented parametrically by: : such that where units is the length arc from the point to the point on . Then a vector equation of is : At a point on : : Therefore, : Because , we can evaluate and because . Thus :Example 2
Let's say we wanted to evaluate the flux of the followingvector field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and dire ...
defined by bounded by the following inequalities:
:
By the divergence theorem,
:
We now need to determine the divergence of . If is a three-dimensional vector field, then the divergence of is given by .
Thus, we can set up the following flux integral
as follows:
:
Now that we have set up the integral, we can evaluate it.
:
Generalizations
Multiple dimensions
One can use the generalised Stokes' theorem to equate the -dimensional volume integral of the divergence of a vector field over a region to the -dimensional surface integral of over the boundary of : : This equation is also known as the divergence theorem. When , this is equivalent toGreen's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region (surface in \R^2) bounded by . It is the two-dimensional special case of Stokes' theorem (surface in \R^3) ...
.
When , it reduces to the fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of derivative, differentiating a function (mathematics), function (calculating its slopes, or rate of change at every point on its domain) with the concept of integral, inte ...
, part 2.
Tensor fields
Writing the theorem inEinstein notation
In mathematics, especially the usage of linear algebra in mathematical physics and differential geometry, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies ...
:
:
suggestively, replacing the vector field with a rank- tensor field , this can be generalized to:
:
where on each side, tensor contraction occurs for at least one index. This form of the theorem is still in 3d, each index takes values 1, 2, and 3. It can be generalized further still to higher (or lower) dimensions (for example to 4d spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
in general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
see for example: , and
).
See also
* Kelvin–Stokes theorem * Generalized Stokes theorem *Differential form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications ...
References
External links
*Differential Operators and the Divergence Theorem
at MathPages
The Divergence (Gauss) Theorem
by Nick Bykov,
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an Open source, open-source collection of Interactive computing, interactive programmes called Demonstrations. It is hosted by Wolfram Research. At its launch, it contained 1300 demonstrations but has grown t ...
.
* – This article was originally based on the GFDL article from PlanetMath
PlanetMath is a free content, free, collaborative, mathematics online encyclopedia. Intended to be comprehensive, the project is currently hosted by the University of Waterloo. The site is owned by a US-based nonprofit corporation, "PlanetMath.org ...
at https://web.archive.org/web/20021029094728/http://planetmath.org/encyclopedia/Divergence.html
{{Calculus topics
Theorems in calculus