|
Helicity Basis
In the Standard Model, using quantum field theory it is conventional to use the helicity basis to simplify calculations (of cross sections, for example). In this basis, the spin is quantized along the axis in the direction of motion of the particle. Spinors The two-component helicity eigenstates \xi_\lambda satisfy :\sigma \cdot \hat \xi_\lambda\left(\hat\right) = \lambda \xi_\lambda\left(\hat\right) \, :where ::\sigma \, are the Pauli matrices, ::\hat \, is the direction of the fermion momentum, ::\lambda = \pm 1 \, depending on whether spin is pointing in the same direction as \hat \, or opposite. To say more about the state, \xi_\lambda \, we will use the generic form of fermion four-momentum: :p^\mu = \left(E, \left, \vec\ \sin \cos, \left, \vec\ \sin \sin, \left, \vec\ \cos \right) \, Then one can say the two helicity eigenstates are :\xi_(\vec) = \frac \begin \left, \vec\ + p_z\\ p_x + i p_y \end = \begin \cos \\ e^\sin \end\, and : \xi_(\vec) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
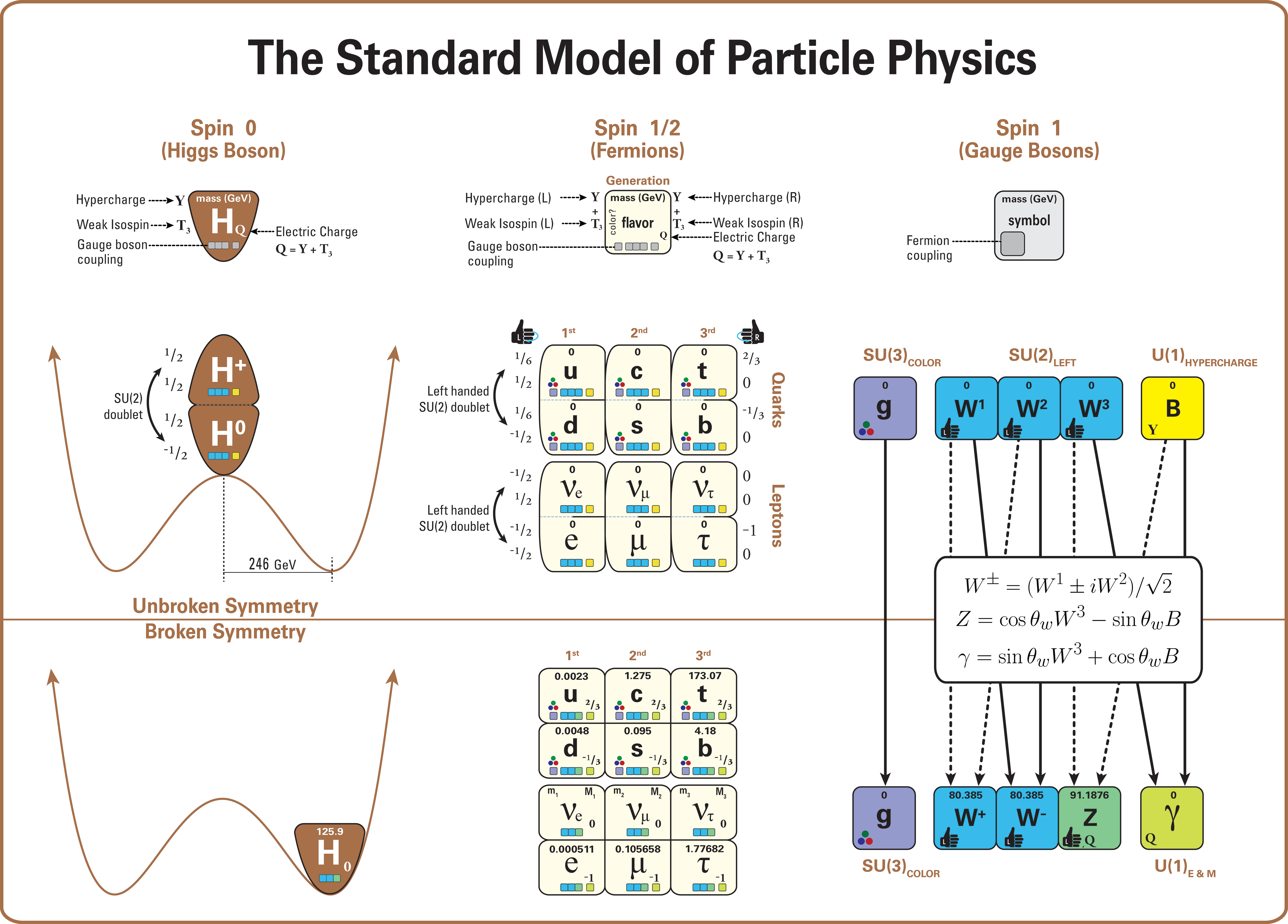
Standard Model (mathematical Formulation)
This article describes the mathematics of the Standard Model of particle physics, a gauge quantum field theory containing the internal symmetries of the unitary product group . The theory is commonly viewed as describing the fundamental set of particles – the leptons, quarks, gauge bosons and the Higgs boson. The Standard Model is renormalizable and mathematically self-consistent; however, despite having huge and continued successes in providing experimental predictions, it does leave some unexplained phenomena. In particular, although the physics of special relativity is incorporated, general relativity is not, and the Standard Model will fail at energies or distances where the graviton is expected to emerge. Therefore, in a modern field theory context, it is seen as an effective field theory. Quantum field theory The standard model is a quantum field theory, meaning its fundamental objects are ''quantum fields'', which are defined at all points in spacetime. Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Section (physics)
In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process. When two discrete particles interact in classical physics, their mutual cross section is the area transverse to their relative motion within which they must meet in order to scatter from each other. If the particles are hard inelastic sphere A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin (physics)
Spin is an Intrinsic and extrinsic properties, intrinsic form of angular momentum carried by elementary particles, and thus by List of particles#Composite particles, composite particles such as hadrons, atomic nucleus, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The relativistic spin–statistics theorem connects electron spin quantization to the Pauli exclusion principle: observations of exclusion imply half-integer spin, and observations of half-integer spin imply exclusion. Spin is described mathematically as a vector for some particles such as photons, and as a spinor or bispinor for other particles such as electrons. Sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Chirality
In chemistry, axial chirality is a special case of chirality (chemistry), chirality in which a molecule contains two pairs of chemical groups in a non-planar arrangement about an axis of chirality so that the molecule is not superposable on its mirror image. The axis of chirality (or ''chiral axis'') is usually determined by a chemical bond that is constrained against free rotation either by steric hindrance of the groups, as in substituted aryl, biaryl compounds such as BINAP, or by Torsion constant#Torsional_stiffness, torsional stiffness of the bonds, as in the C=C double bonds in allenes such as glutinic acid. Axial chirality is most commonly observed in substituted biaryl compounds wherein the rotation about the aryl–aryl bond is restricted so it results in chiral atropisomers, as in various ortho-substituted biphenyls, and in binaphthyls such as BINAP. Axial chirality differs from Stereocenter, central chirality (point chirality) in that axial chirality does not require a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenstate
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Matrices
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () when used in connection with isospin symmetries. \begin \sigma_1 = \sigma_x &= \begin 0&1\\ 1&0 \end, \\ \sigma_2 = \sigma_y &= \begin 0& -i \\ i&0 \end, \\ \sigma_3 = \sigma_z &= \begin 1&0\\ 0&-1 \end. \\ \end These matrices are named after the physicist Wolfgang Pauli. In quantum mechanics, they occur in the Pauli equation, which takes into account the interaction of the spin of a particle with an external electromagnetic field. They also represent the interaction states of two polarization filters for horizontal/vertical polarization, 45 degree polarization (right/left), and circular polarization (right/left). Each Pauli matrix is Hermitian, and together w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles include all quarks and leptons and all composite particles made of an even and odd, odd number of these, such as all baryons and many atoms and atomic nucleus, nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in Theory of relativity, relativistic quantum field theory, particles with integer Spin (physics), spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-momentum
In special relativity, four-momentum (also called momentum–energy or momenergy) is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant vector, contravariant four-momentum of a particle with relativistic energy and three-momentum , where is the particle's three-velocity and the Lorentz factor, is p = \left(p^0 , p^1 , p^2 , p^3\right) = \left(\frac E c , p_x , p_y , p_z\right). The quantity of above is the ordinary Momentum#Single particle, non-relativistic momentum of the particle and its rest mass. The four-momentum is useful in relativistic calculations because it is a Lorentz covariant vector. This means that it is easy to keep track of how it transforms under Lorentz transformations. Minkowski norm Calculating the Minkowski space#Mathematical structure, Minkowski norm squared of the four-momentum gives a Loren ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Creation And Annihilation Operators
Creation operators and annihilation operators are Operator (mathematics), mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator (usually denoted \hat) lowers the number of particles in a given state by one. A creation operator (usually denoted \hat^\dagger) increases the number of particles in a given state by one, and it is the Hermitian adjoint, adjoint of the annihilation operator. In many subfields of physics and chemistry, the use of these operators instead of wavefunctions is known as second quantization. They were introduced by Paul Dirac. Creation and annihilation operators can act on states of various types of particles. For example, in quantum chemistry and many-body theory the creation and annihilation operators often act on electron states. They can also refer specifically to the ladder operators for the quantum harmonic oscillator. In the la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Spinor
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group. Dirac spinors are important and interesting in numerous ways. Foremost, they are important as they do describe all of the known fundamental particle fermions in nature; this includes the electron and the quarks. Algebraically they behave, in a certain sense, as the "square root" of a vector. This is not readily apparent from direct examination, but it has slowly become clear over the last 60 years that spinorial representations are fundamental to geometry. For example, effectively all Riemannian manifolds can have spinors and spin connections built upon them, via the Clifford algebra. The Dirac spinor is specific to t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl Basis
In mathematical physics, the gamma matrices, \ \left\\ , also called the Dirac matrices, are a set of conventional matrices with specific commutation relation, anticommutation relations that ensure they generating set, generate a matrix representation of the Clifford algebra \ \mathrm_(\mathbb) ~. It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonality, orthogonal basis vectors for covariance and contravariance of vectors, contravariant vector (mathematics and physics), vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime algebra, spacetime acts. This in turn makes it possible to represent infinitesimal rotation, spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin-1/2, particles. Gamma matrices wer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |