|
Hamilton–Jacobi–Bellman Equation
The Hamilton-Jacobi-Bellman (HJB) equation is a nonlinear partial differential equation that provides necessary and sufficient conditions for optimality of a control with respect to a loss function. Its solution is the value function of the optimal control problem which, once known, can be used to obtain the optimal control by taking the maximizer (or minimizer) of the Hamiltonian involved in the HJB equation. The equation is a result of the theory of dynamic programming which was pioneered in the 1950s by Richard Bellman and coworkers. The connection to the Hamilton–Jacobi equation from classical physics was first drawn by Rudolf Kálmán. In discrete-time problems, the analogous difference equation is usually referred to as the Bellman equation. While classical variational problems, such as the brachistochrone problem, can be solved using the Hamilton–Jacobi–Bellman equation, the method can be applied to a broader spectrum of problems. Further it can be generalized to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Partial Differential Equation
In mathematics and physics, a nonlinear partial differential equation is a partial differential equation with nonlinear system, nonlinear terms. They describe many different physical systems, ranging from gravitation to fluid dynamics, and have been used in mathematics to solve problems such as the Poincaré conjecture and the Calabi conjecture. They are difficult to study: almost no general techniques exist that work for all such equations, and usually each individual equation has to be studied as a separate problem. The distinction between a linear and a nonlinear partial differential equation is usually made in terms of the properties of the Operator (mathematics), operator that defines the PDE itself. Methods for studying nonlinear partial differential equations Existence and uniqueness of solutions A fundamental question for any PDE is the existence and uniqueness of a solution for given boundary conditions. For nonlinear equations these questions are in general very hard: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
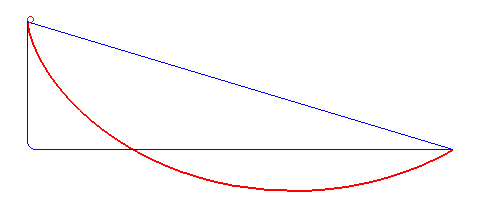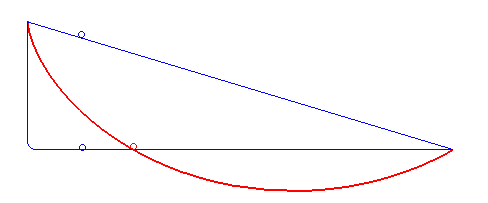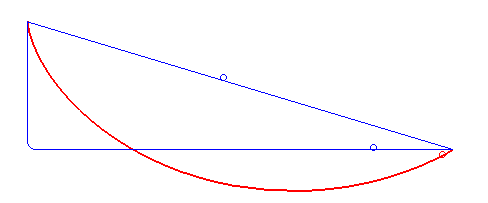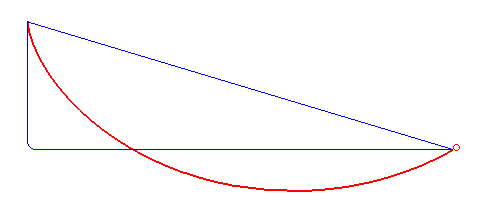
Brachistochrone Problem
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696 and solved by Isaac Newton in 1697. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a Cusp (singularity), cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimax Solution
Minimax (sometimes Minmax, MM or saddle point) is a decision rule used in artificial intelligence, decision theory, combinatorial game theory, statistics, and philosophy for ''minimizing'' the possible loss for a worst case (''max''imum loss) scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty. Game theory In general games The maximin value is the highest value that the player can be sure to get without knowing the actions of the other players; equivalently, it is the lowest value the other players can force the player to receive when they know the player's action. Its formal definition is: :\underline = \max_ \min_ Where: * is the index of the play ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael G
Michael may refer to: People * Michael (given name), a given name * he He ..., a given name * Michael (surname), including a list of people with the surname Michael Given name * Michael (bishop elect)">Michael (surname)">he He ..., a given name * Michael (surname), including a list of people with the surname Michael Given name * Michael (bishop elect), English 13th-century Bishop of Hereford elect * Michael (Khoroshy) (1885–1977), cleric of the Ukrainian Orthodox Church of Canada * Michael Donnellan (fashion designer), Michael Donnellan (1915–1985), Irish-born London fashion designer, often referred to simply as "Michael" * Michael (footballer, born 1982), Brazilian footballer * Michael (footballer, born 1983), Brazilian footballer * Michael (footballer, born 1993), Brazilian footballer * Michael (footballer, born February 1996), Brazilian footballer * Michael (footballer, born March 1996), Brazilian footballer * Michael (footballer, born 1999), Brazilian football ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pierre-Louis Lions
Pierre-Louis Lions (; born 11 August 1956) is a French mathematician. He is known for a number of contributions to the fields of partial differential equations and the calculus of variations. He was a recipient of the 1994 Fields Medal and the 1991 Prize of the Philip Morris tobacco and cigarette company. Biography Lions entered the École normale supérieure in 1975, and received his doctorate from the University of Pierre and Marie Curie in 1979. He holds the position of Professor of '' Partial differential equations and their applications'' at the Collège de France in Paris as well as a position at École Polytechnique. Since 2014, he has also been a visiting professor at the University of Chicago. In 1979, Lions married Lila Laurenti, with whom he has one son. Lions' parents were Andrée Olivier and the renowned mathematician Jacques-Louis Lions, at the time a professor at the University of Nancy. Awards and honors In 1994, while working at the Paris Dauphine Universi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backward Induction
Backward induction is the process of determining a sequence of optimal choices by reasoning from the endpoint of a problem or situation back to its beginning using individual events or actions. Backward induction involves examining the final point in a series of decisions and identifying the optimal process or action required to arrive at that point. This process continues backward until the best action for every possible point along the sequence is determined. Backward induction was first utilized in 1875 by Arthur Cayley, who discovered the method while attempting to solve the secretary problem. In dynamic programming, a method of mathematical optimization, backward induction is used for solving the Bellman equation. In the related fields of automated planning and scheduling and automated theorem proving, the method is called backward search or backward chaining. In chess, it is called retrograde analysis. In game theory, a variant of backward induction is used to compute subgame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Little-o Notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '' Ordnung'', meaning the order of approximation. In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; one well-known example is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates. Big O notation characterizes functions according to their growth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Expansion
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
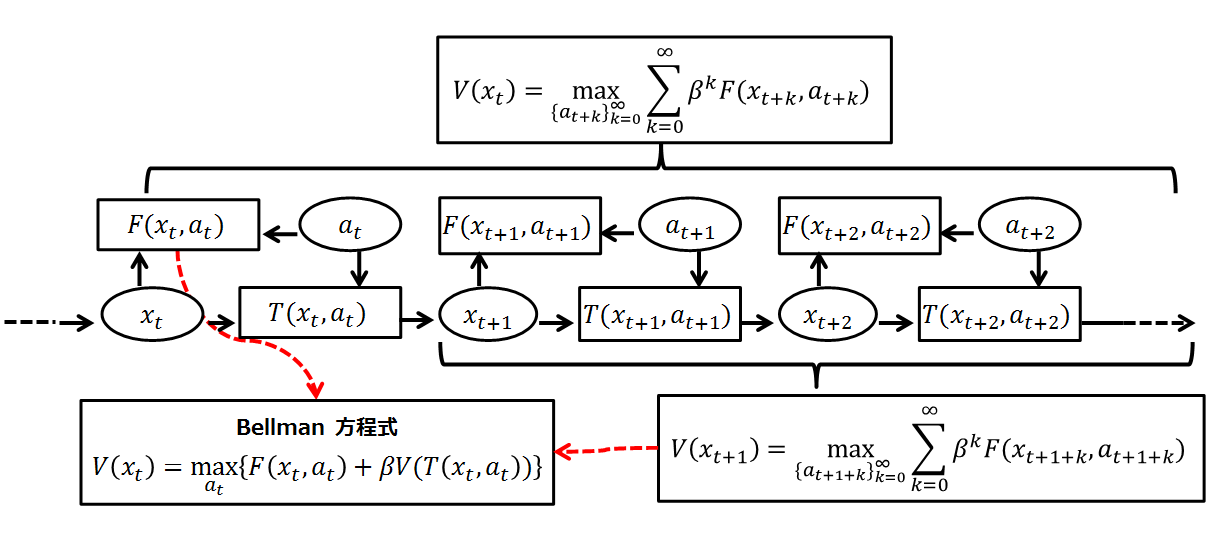
Principle Of Optimality
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ''Theory of Games and Eco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bequest Value
Bequest value, in economics, is the Value (economics), value of satisfaction from preserving a natural environment or a historic environment, in other words natural heritage or cultural heritage for future generations. It is often used when estimating the value of an environmental service or good. Together with the existence value, it makes up the non-use value of such an environmental service or good. References Environmental economics {{econ-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subderivative
In mathematics, the subderivative (or subgradient) generalizes the derivative to convex functions which are not necessarily differentiable. The set of subderivatives at a point is called the subdifferential at that point. Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization. Let f:I \to \mathbb be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function f(x)=, x, is non-differentiable when x=0. However, as seen in the graph on the right (where f(x) in blue has non-differentiable kinks similar to the absolute value function), for any x_0 in the domain of the function one can draw a line which goes through the point (x_0,f(x_0)) and which is everywhere either touching or below the graph of ''f''. The slope of such a line is called a ''subderivative''. Definition Rigorously, a ''subderivative'' of a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosity Solution
In mathematics, the viscosity solution concept was introduced in the early 1980s by Pierre-Louis Lions and Michael G. Crandall as a generalization of the classical concept of what is meant by a 'solution' to a partial differential equation (PDE). It has been found that the viscosity solution is the natural solution concept to use in many applications of PDE's, including for example first order equations arising in dynamic programming (the Hamilton–Jacobi–Bellman equation), differential games (the Hamilton–Jacobi–Isaacs equation) or front evolution problems, as well as second-order equations such as the ones arising in stochastic optimal control or stochastic differential games. The classical concept was that a PDE : F(x,u,Du,D^2 u) = 0 over a domain x\in\Omega has a solution if we can find a function ''u''(''x'') continuous and differentiable over the entire domain such that x, u, Du, D^2 u satisfy the above equation at every point. If a scalar equation is degenerate el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |