 |
Guillotine Problem
Guillotine cutting is the process of producing small rectangular items of fixed dimensions from a given large rectangular sheet, using only guillotine-cuts. A guillotine-cut (also called an edge-to-edge cut) is a straight bisecting line going from one edge of an existing rectangle to the opposite edge, similarly to a paper guillotine. Guillotine cutting is particularly common in the glass industry. Glass sheets are scored along horizontal and vertical lines, and then broken along these lines to obtain smaller panels. It is also useful for cutting steel plates, cutting of wood sheets to make furniture, and cutting of cardboard into boxes. There are various optimization problems related to guillotine cutting, such as: maximize the total area of the produced pieces, or their total value; minimize the amount of waste (unused parts) of the large sheet, or the total number of sheets. They have been studied in combinatorial geometry, operations research and industrial engineering. A re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Strip Packing Problem
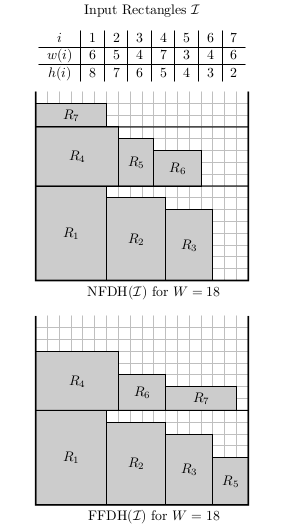
The strip packing problem is a 2-dimensional geometric minimization problem. Given a set of axis-aligned rectangles and a strip of bounded width and infinite height, determine an overlapping-free packing of the rectangles into the strip, minimizing its height. This problem is a cutting and packing problem and is classified as an ''Open Dimension Problem'' according to Wäscher et al. This problem arises in the area of scheduling, where it models jobs that require a contiguous portion of the memory over a given time period. Another example is the area of industrial manufacturing, where rectangular pieces need to be cut out of a sheet of material (e.g., cloth or paper) that has a fixed width but infinite length, and one wants to minimize the wasted material. This problem was first studied in 1980. It is strongly-NP hard and there exists no polynomial-time approximation algorithm with a ratio smaller than 3/2 unless P = NP. However, the best approximation ratio achieved so far (by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Hamiltonian Circuit
In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. The computational problems of determining whether such paths and cycles exist in graphs are NP-complete; see Hamiltonian path problem for details. Hamiltonian paths and cycles are named after William Rowan Hamilton, who invented the icosian game, now also known as ''Hamilton's puzzle'', which involves finding a Hamiltonian cycle in the edge graph of the dodecahedron. Hamilton solved this problem using the icosian calculus, an algebraic structure based on roots of unity with many similarities to the quaternions (also inve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Best-first Search
Best-first search is a class of search algorithms which explores a graph by expanding the most promising node chosen according to a specified rule. Judea Pearl described best-first search as estimating the promise of node ''n'' by a "heuristic evaluation function f(n) which, in general, may depend on the description of ''n'', the description of the goal, the information gathered by the search up to that point, and most importantly, on any extra knowledge about the problem domain." Some authors have used "best-first search" to refer specifically to a search with a heuristic that attempts to predict how close the end of a path is to a solution (or, goal), so that paths which are judged to be closer to a solution (or, goal) are expanded first. This specific type of search is called '' greedy best-first search'' or ''pure heuristic search''. Efficient selection of the current best candidate for extension is typically implemented using a priority queue. The A* search algorithm is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Branch And Bound
Branch and bound (BB, B&B, or BnB) is a method for solving optimization problems by breaking them down into smaller sub-problems and using a bounding function to eliminate sub-problems that cannot contain the optimal solution. It is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores ''branches'' of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated ''bounds'' on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm. The algorithm depends on efficient estimation of the lower and u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Heuristic (computer Science)
A heuristic or heuristic technique (''problem solving'', ''Heuristic (psychology), mental shortcut'', ''rule of thumb'') is any approach to problem solving that employs a Pragmatism, pragmatic method that is not fully Mathematical optimisation, optimized, perfected, or Rationality, rationalized, but is nevertheless "good enough" as an approximation or attribute substitution. Where finding an optimal solution is impossible or impractical, heuristic methods can be used to speed up the process of finding a satisfactory solution. Heuristics can be mental shortcuts that ease the cognitive load of Decision-making, making a decision. Context Gigerenzer & Gaissmaier (2011) state that Set (mathematics), sub-sets of ''strategy'' include heuristics, regression analysis, and Bayesian inference. Heuristics are strategies based on rules to generate optimal decisions, like the anchoring effect and utility maximization problem. These strategies depend on using readily accessible, thoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Tree Search
In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well. Types Unlike linked lists, one-dimensional arrays and other linear data structures, which are canonically traversed in linear order, trees may be traversed in multiple ways. They may be traversed in depth-first or breadth-first order. There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order. Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth-first search. The latter, as well as breadth-first search, can also be used t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Recursion
Recursion occurs when the definition of a concept or process depends on a simpler or previous version of itself. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function (mathematics), function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no infinite loop or infinite chain of references can occur. A process that exhibits recursion is ''recursive''. Video feedback displays recursive images, as does an infinity mirror. Formal definitions In mathematics and computer science, a class of objects or methods exhibits recursive behavior when it can be defined by two properties: * A simple ''base case'' (or cases) — a terminating scenario that does not use recursion to produce an answer * A ''recursive step'' — a set of rules that reduce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Approximation Algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Exact Algorithm
In computer science and operations research, exact algorithms are algorithms that always solve an optimization problem to optimality. Unless P = NP, an exact algorithm for an NP-hardness , NP-hard optimization problem cannot run in worst-case polynomial time. There has been extensive research on finding exact algorithms whose running time is exponential with a low base. See also * Approximation-preserving reduction * APX is the class of problems with some constant-factor approximation algorithm * Heuristic algorithm * Polynomial-time approximation scheme, PTAS - a type of approximation algorithm that takes the approximation ratio as a parameter References {{reflist Computational complexity theory Optimization algorithms and methods ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |