|
Group Delay And Phase Delay
In signal processing, group delay and phase delay are functions that describe in different ways the delay times experienced by a signal’s various sinusoidal frequency components as they pass through a linear time-invariant (LTI) system (such as a microphone, coaxial cable, amplifier, loudspeaker, communications system, ethernet cable, digital filter, or analog filter). Unfortunately, these delays are sometimes frequency dependent, which means that different sinusoid frequency components experience different time delays. As a result, the signal's waveform experiences distortion as it passes through the system. This distortion can cause problems such as poor fidelity in analog video and analog audio, or a high bit-error rate in a digital bit stream. Background Frequency components of a signal Fourier analysis reveals how signals in time can alternatively be expressed as the sum of sinusoidal frequency components, each based on the trigonometric function \sin(x) with a fixed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
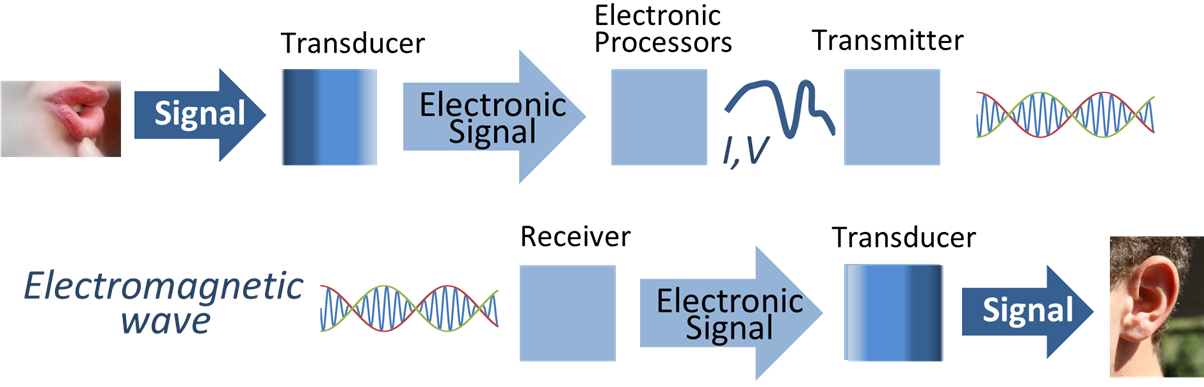
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Units Of Time
A unit of time is any particular time interval, used as a standard way of measuring or expressing duration. The SI base unit, base unit of time in the International System of Units (SI), and by extension most of the Western world, is the second, defined as about 9 billion oscillations of the caesium atom. The exact modern SI definition is "[The second] is defined by taking the fixed numerical value of the cesium frequency, , the unperturbed ground-state hyperfine transition frequency of the cesium 133 atom, to be when expressed in the unit Hz, which is equal to s−1." Historically, many units of time were defined by the movements of astronomical objects. * Sun-based: the year is based on the Earth's orbit, Earth's orbital period around the sun. Historical year-based units include the Olympiad (four years), the lustrum (five years), the indiction (15 years), the decade, the century, and the millennium. * Moon-based: the month is based on the Orbit of the Moon, Moon's orbital per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radians
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that subtends an arc whose length equals the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Units
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude or quantity of these types of geometric figures and in this context an angle consists of a number and unit of measurement. Angular measure or measure of angle are sometimes used to distinguish between the measurement and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
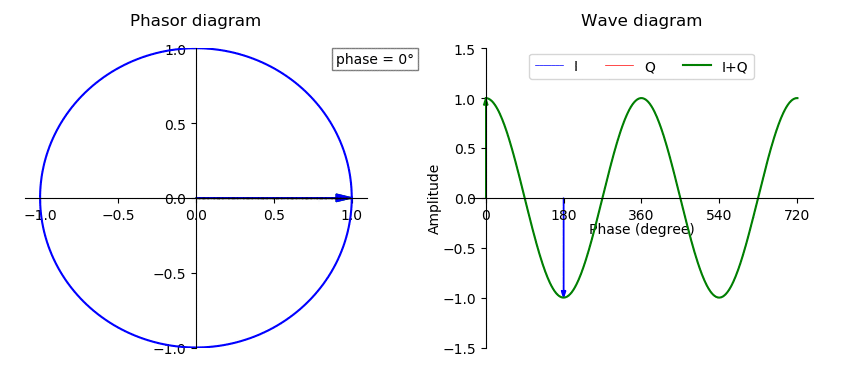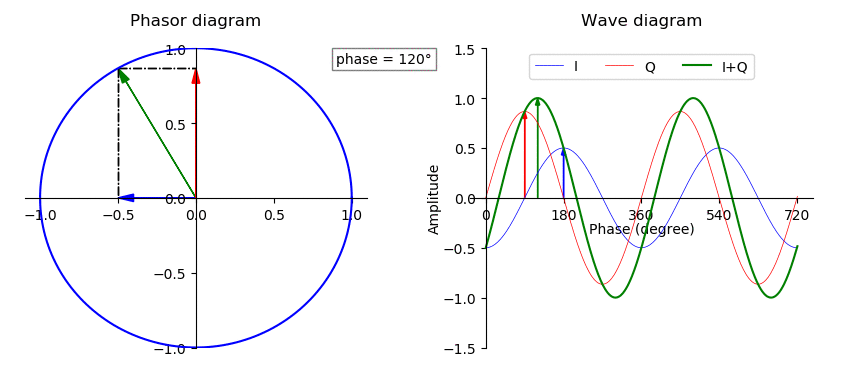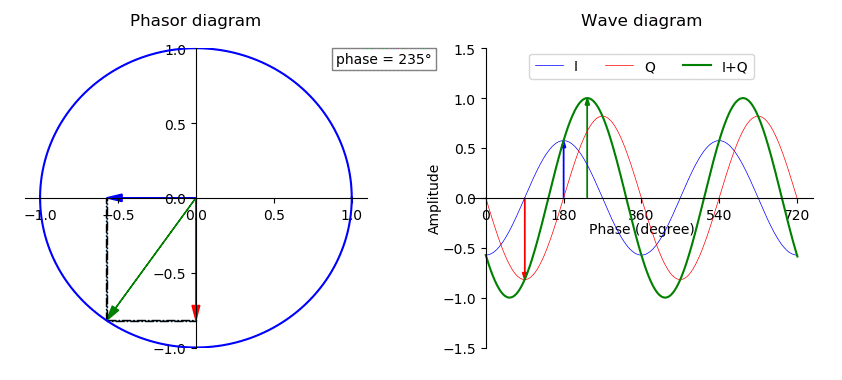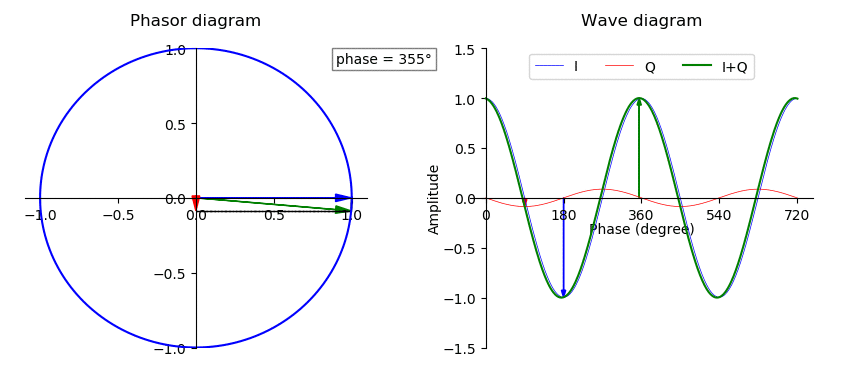
Phase Shift
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Response
In signal processing, phase response is the relationship between the phase of a sinusoidal input and the output signal passing through any device that accepts input and produces an output signal, such as an amplifier An amplifier, electronic amplifier or (informally) amp is an electronic device that can increase the magnitude of a signal (a time-varying voltage or current). It is a two-port electronic circuit that uses electric power from a power su ... or a filter. Amplifiers, filters, and other devices are often categorized by their amplitude and/or phase response. The amplitude response is the ratio of output amplitude to input, usually a function of the frequency. Similarly, phase response is the phase of the output with the input as reference. The input is defined as zero phase. A phase response is not limited to lying between 0° and 360°, as phase can accumulate to any amount of time. See also * Group delay and phase delay References Trigonometry Wav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Components Of A Signal
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. The interval of time between events is called the period. It is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times per minute (2 hertz), its period is one half of a second. Special definitions of frequency are used in certain contexts, such as the angular frequency in rotational or cyclical properties, when the rate of angular progress is measured. Spatial frequency is defined for properties that vary or cccur repeatedly in geometry or space. The unit of measurement of frequency in the International System of Units (SI) is the hertz, having the symbol Hz. Definitions and units For cyclical phenomena such as oscillations, waves, or for examples o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'', and input ''B'' produces response ''Y'', then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1 + x_2) = F(x_1) + F(x_2) and homogeneity F(ax) = a F(x) for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearity
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a '' polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are '' nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time-invariant System
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of Linear system#Definition, linearity and Time-invariant system, time-invariance; these terms are briefly defined in the overview below. These properties apply (exactly or approximately) to many important physical systems, in which case the response of the system to an arbitrary input can be found directly using convolution: where is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication). What's more, there are systematic methods for solving any such system (determining ), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers. Linear time-invariant system theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |