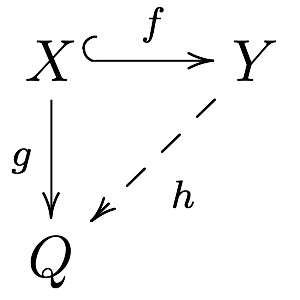|
Group Cohomology
In mathematics (more specifically, in homological algebra), group cohomology is a set of mathematical tools used to study groups using cohomology theory, a technique from algebraic topology. Analogous to group representations, group cohomology looks at the group actions of a group ''G'' in an associated ''G''-module ''M'' to elucidate the properties of the group. By treating the ''G''-module as a kind of topological space with elements of G^n representing ''n''- simplices, topological properties of the space may be computed, such as the set of cohomology groups H^n(G,M). The cohomology groups in turn provide insight into the structure of the group ''G'' and ''G''-module ''M'' themselves. Group cohomology plays a role in the investigation of fixed points of a group action in a module or space and the quotient module or space with respect to a group action. Group cohomology is used in the fields of abstract algebra, homological algebra, algebraic topology and algebraic number th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eilenberg–MacLane Space
In mathematics, specifically algebraic topology, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without a space), and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. (See e.g. ) In this context it is therefore conventional to write the name without a space. is a topological space with a single nontrivial homotopy group. Let ''G'' be a group and ''n'' a positive integer. A connected topological space ''X'' is called an Eilenberg–MacLane space of type K(G,n), if it has ''n''-th homotopy group \pi_n(X) isomorphic to ''G'' and all other homotopy groups trivial. Assuming that ''G'' is abelian in the case that n > 1, Eilenberg–MacLane spaces of type K(G,n) always exist, and are all weak homotopy equivalent. Thus, one may consider K(G,n) as referring to a weak homotopy equivalence class of spaces. It is common to refer to any representative as "a K(G,n)" or as "a model of K(G,n)". Moreover, it is comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Module (mathematics)
In mathematics, a module is a generalization of the notion of vector space in which the field of scalars is replaced by a (not necessarily commutative) ring. The concept of a ''module'' also generalizes the notion of an abelian group, since the abelian groups are exactly the modules over the ring of integers. Like a vector space, a module is an additive abelian group, and scalar multiplication is distributive over the operations of addition between elements of the ring or module and is compatible with the ring multiplication. Modules are very closely related to the representation theory of groups. They are also one of the central notions of commutative algebra and homological algebra, and are used widely in algebraic geometry and algebraic topology. Introduction and definition Motivation In a vector space, the set of scalars is a field and acts on the vectors by scalar multiplication, subject to certain axioms such as the distributive law. In a module, the scal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Injective Object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object. Definition An object Q in a category \mathbf is said to be injective if for every monomorphism f: X \to Y and every morphism g: X \to Q there exists a morphism h: Y \to Q extending g to Y, i.e. such that h \circ f = g. That is, every morphism X \to Q factors through every monomorphism X \hookrightarrow Y. The morphism h in the above definition is not required to be uniquely determined by f and g. In a locally small category, it is equivalent to require that the hom functor \operatorname_(-,Q) carries monomorphisms in \mathbf to surjective set maps. In Abelian categories The notion of injectivity was first formulated for abelian categories, and this is still one of its primary areas of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derived Functor
In mathematics, certain functors may be ''derived'' to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics. Motivation It was noted in various quite different settings that a short exact sequence often gives rise to a "long exact sequence". The concept of derived functors explains and clarifies many of these observations. Suppose we are given a covariant left exact functor ''F'' : A → B between two abelian categories A and B. If 0 → ''A'' → ''B'' → ''C'' → 0 is a short exact sequence in A, then applying ''F'' yields the exact sequence 0 → ''F''(''A'') → ''F''(''B'') → ''F''(''C'') and one could ask how to continue this sequence to the right to form a long exact sequence. Strictly speaking, this question is ill-posed, since there are always numerous different ways to continue a given exact sequence to the right. But it turns out that (if A is "nice" enough) t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Left Exact Functor
In mathematics, particularly homological algebra, an exact functor is a functor that preserves short exact sequences. Exact functors are convenient for algebraic calculations because they can be directly applied to presentations of objects. Much of the work in homological algebra is designed to cope with functors that ''fail'' to be exact, but in ways that can still be controlled. Definitions Let P and Q be abelian categories, and let be a covariant additive functor (so that, in particular, ''F''(0) = 0). We say that ''F'' is an exact functor if whenever :0 \to A \ \stackrel \ B \ \stackrel \ C \to 0 is a short exact sequence in P then :0 \to F(A) \ \stackrel \ F(B)\ \stackrel \ F(C) \to 0 is a short exact sequence in Q. (The maps are often omitted and implied, and one says: "if 0→''A''→''B''→''C''→0 is exact, then 0→''F''(''A'')→''F''(''B'')→''F''(''C'')→0 is also exact".) Further, we say that ''F'' is *left-exact if whenever 0→''A''→''B''� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functor
In mathematics, specifically category theory, a functor is a Map (mathematics), mapping between Category (mathematics), categories. Functors were first considered in algebraic topology, where algebraic objects (such as the fundamental group) are associated to topological spaces, and maps between these algebraic objects are associated to continuous function, continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied. The words ''category'' and ''functor'' were borrowed by mathematicians from the philosophers Aristotle and Rudolf Carnap, respectively. The latter used ''functor'' in a Linguistics, linguistic context; see function word. Definition Let ''C'' and ''D'' be category (mathematics), categories. A functor ''F'' from ''C'' to ''D'' is a mapping that * associates each Mathematical object, object X in ''C'' to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Homomorphisms
In mathematics, given two groups, (''G'',∗) and (''H'', ·), a group homomorphism from (''G'',∗) to (''H'', ·) is a function ''h'' : ''G'' → ''H'' such that for all ''u'' and ''v'' in ''G'' it holds that : h(u*v) = h(u) \cdot h(v) where the group operation on the left side of the equation is that of ''G'' and on the right side that of ''H''. From this property, one can deduce that ''h'' maps the identity element ''eG'' of ''G'' to the identity element ''eH'' of ''H'', : h(e_G) = e_H and it also maps inverses to inverses in the sense that : h\left(u^\right) = h(u)^. \, Hence one can say that ''h'' "is compatible with the group structure". In areas of mathematics where one considers groups endowed with additional structure, a ''homomorphism'' sometimes means a map which respects not only the group structure (as above) but also the extra structure. For example, a homomorphism of topological groups is often required to be continuous. Properties Let e_ be the identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivariant Map
In mathematics, equivariance is a form of symmetry for function (mathematics), functions from one space with symmetry to another (such as symmetric spaces). A function is said to be an equivariant map when its domain and codomain are Group action (mathematics), acted on by the same symmetry group, and when the function commutative property, commutes with the action of the group. That is, applying a symmetry transformation and then computing the function produces the same result as computing the function and then applying the transformation. Equivariant maps generalize the concept of Invariant (mathematics), invariants, functions whose value is unchanged by a symmetry transformation of their argument. The value of an equivariant map is often (imprecisely) called an invariant. In statistical inference, equivariance under statistical transformations of data is an important property of various estimation methods; see invariant estimator for details. In pure mathematics, equivariance is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory is used in most areas of mathematics. In particular, many constructions of new mathematical objects from previous ones that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient space (other), quotient spaces, direct products, completion, and duality (mathematics), duality. Many areas of computer science also rely on category theory, such as functional programming and Semantics (computer science), semantics. A category (mathematics), category is formed by two sorts of mathematical object, objects: the object (category theory), objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. Metapho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long Exact Sequence
In mathematics, an exact sequence is a sequence of morphisms between objects (for example, Group (mathematics), groups, Ring (mathematics), rings, Module (mathematics), modules, and, more generally, objects of an abelian category) such that the Image (mathematics), image of one morphism equals the kernel (algebra), kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Sequence
In mathematics, an exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i |