|
Greibach Normal Form
In formal language theory, a context-free grammar is in Greibach normal form (GNF) if the right-hand sides of all production rules start with a terminal symbol, optionally followed by some non-terminals. A non-strict form allows one exception to this format restriction for allowing the empty word (epsilon, ε) to be a member of the described language. The normal form was established by Sheila Greibach and it bears her name. More precisely, a context-free grammar is in Greibach normal form, if all production rules are of the form: :A \to a A_1 A_2 \cdots A_n where A is a nonterminal symbol, a is a terminal symbol, and A_1 A_2 \ldots A_n is a (possibly empty) sequence of nonterminal symbols. Observe that the grammar does not have left recursions. Every context-free grammar can be transformed into an equivalent grammar in Greibach normal form. Various constructions exist. Some do not permit the second form of rule and cannot transform context-free grammars that can generate the emp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Formal Language
In logic, mathematics, computer science, and linguistics, a formal language is a set of strings whose symbols are taken from a set called "alphabet". The alphabet of a formal language consists of symbols that concatenate into strings (also called "words"). Words that belong to a particular formal language are sometimes called ''well-formed words''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar. In computer science, formal languages are used, among others, as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages, in which the words of the language represent concepts that are associated with meanings or semantics. In computational complexity theory, decision problems are typically defined as formal languages, and complexity classes are defined as the sets of the formal languages that can be parsed by machines with limited computational power. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Context-free Grammar
In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form : A\ \to\ \alpha with A a ''single'' nonterminal symbol, and \alpha a string of terminals and/or nonterminals (\alpha can be empty). Regardless of which symbols surround it, the single nonterminal A on the left hand side can always be replaced by \alpha on the right hand side. This distinguishes it from a context-sensitive grammar, which can have production rules in the form \alpha A \beta \rightarrow \alpha \gamma \beta with A a nonterminal symbol and \alpha, \beta, and \gamma strings of terminal and/or nonterminal symbols. A formal grammar is essentially a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the first rule in the picture, : \lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Production (computer Science)
In computer science, a production or production rule is a rewrite rule that replaces some symbols with other symbols. A finite set of productions P is the main component in the specification of a formal grammar (specifically a generative grammar). The other components are a finite set N of nonterminal symbols, a finite set (known as an alphabet) \Sigma of terminal symbols that is disjoint from N and a distinguished symbol S \in N that is the ''start symbol''. In an unrestricted grammar, a production is of the form u \to v, where u and v are arbitrary strings of terminals and nonterminals, and u may not be the empty string. If v is the empty string, this is denoted by the symbol \epsilon, or \lambda (rather than leaving the right-hand side blank). So productions are members of the cartesian product :V^*NV^* \times V^* = (V^*\setminus\Sigma^*) \times V^*, where V := N \cup \Sigma is the ''vocabulary'', ^ is the Kleene star operator, V^*NV^* indicates concatenation, \cup deno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Terminal Symbol
In formal languages, terminal and nonterminal symbols are parts of the ''vocabulary'' under a formal grammar. ''Vocabulary'' is a finite, nonempty set of symbols. ''Terminal symbols'' are symbols that cannot be replaced by other symbols of the vocabulary. ''Nonterminal symbols'' are symbols that can be replaced by other symbols of the vocabulary by the production rules under the same formal grammar. A formal grammar defines a formal language over the vocabulary of the grammar. In the context of formal language, the term ''vocabulary'' is more commonly known as ''alphabet''. Nonterminal symbols are also called ''syntactic variables''. Terminal symbols Terminal symbols are those symbols that can appear in the formal language defined by a formal grammar. The process of applying the production rules successively to a start symbol might not terminate, but if it terminates when there is no more production rule can be applied, the output string will consist only of terminal symb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Empty Word
In formal language theory, the empty string, or empty word, is the unique string of length zero. Formal theory Formally, a string is a finite, ordered sequence of characters such as letters, digits or spaces. The empty string is the special case where the sequence has length zero, so there are no symbols in the string. There is only one empty string, because two strings are only different if they have different lengths or a different sequence of symbols. In formal treatments, the empty string is denoted with ε or sometimes Λ or λ. The empty string should not be confused with the empty language ∅, which is a formal language (i.e. a set of strings) that contains no strings, not even the empty string. The empty string has several properties: * , ε, = 0. Its string length is zero. * ε ⋅ s = s ⋅ ε = s. The empty string is the identity element of the concatenation operation. The set of all strings forms a free monoid with respect to ⋅ and ε. * εR = ε. Reversal o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sheila Greibach
Sheila Adele Greibach (born 6 October 1939 in New York City) is an American researcher in formal languages in computing, automata, compiler theory and computer science. She is an Emeritus Professor of Computer Science at the University of California, Los Angeles, and notable work include working with Seymour Ginsburg and Michael A. Harrison in context-sensitive parsing using the stack automaton model. Besides establishing the normal form ( Greibach normal form) for context-free grammars, in 1965, she also investigated properties of W-grammars, pushdown automata, and decidability problems. Early career Greibach earned an A.B. degree ( summa cum laude) in Linguistics and Applied Mathematics from Radcliffe College in 1960, and two years after achieved an A.M. degree. In 1963, she was awarded a PhD at Harvard University, advised by Anthony Oettinger with a PhD thesis entitled "Inverses of Phrase Structure Generators". She continued to work at Harvard at the Division of E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
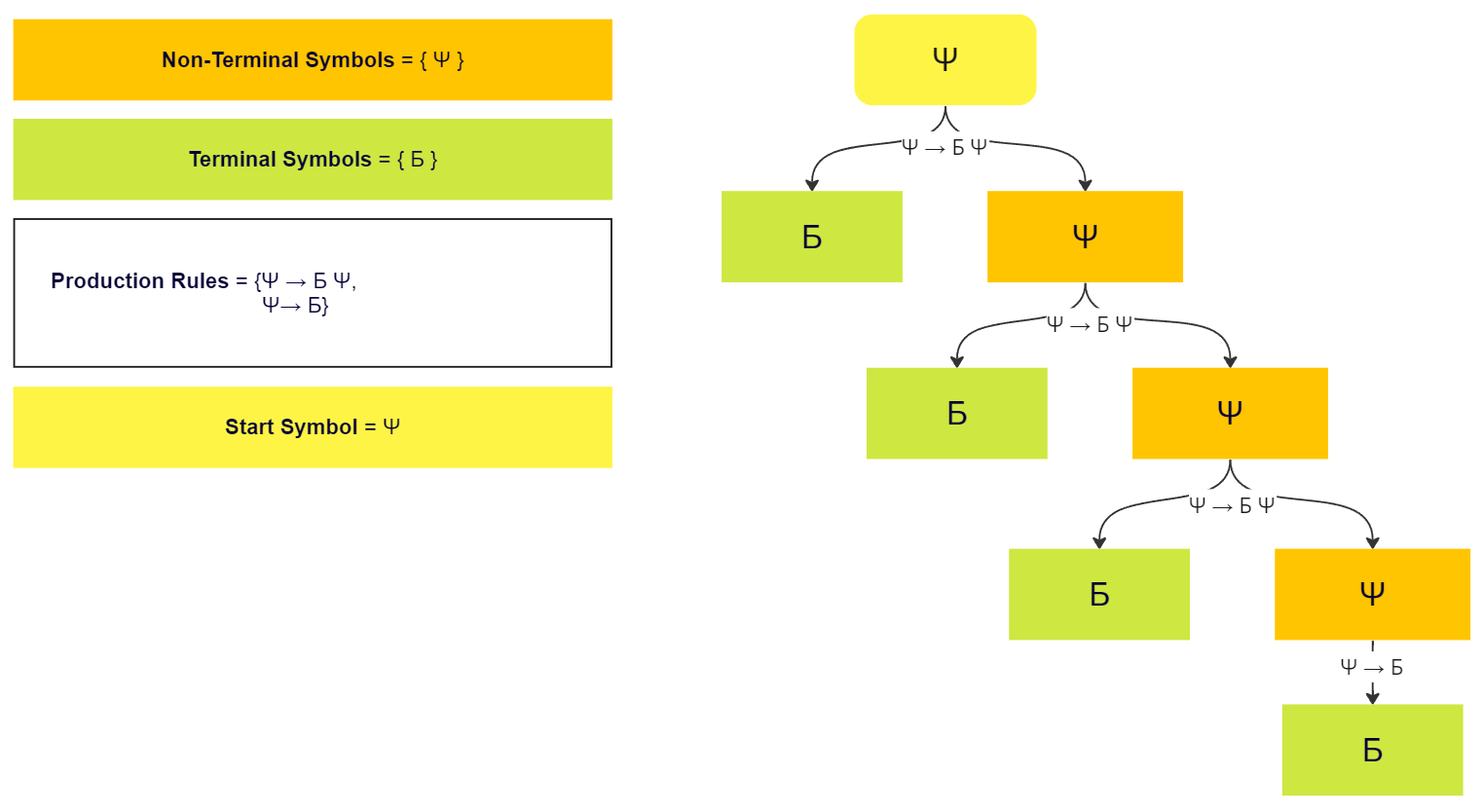 |
Nonterminal Symbol
In formal languages, terminal and nonterminal symbols are parts of the ''vocabulary'' under a formal grammar. ''Vocabulary'' is a finite, nonempty set of symbols. ''Terminal symbols'' are symbols that cannot be replaced by other symbols of the vocabulary. ''Nonterminal symbols'' are symbols that can be replaced by other symbols of the vocabulary by the production rules under the same formal grammar. A formal grammar defines a formal language over the vocabulary of the grammar. In the context of formal language, the term ''vocabulary'' is more commonly known as ''alphabet''. Nonterminal symbols are also called ''syntactic variables''. Terminal symbols Terminal symbols are those symbols that can appear in the formal language defined by a formal grammar. The process of applying the production rules successively to a start symbol might not terminate, but if it terminates when there is no more production rule can be applied, the output string will consist only of terminal symb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
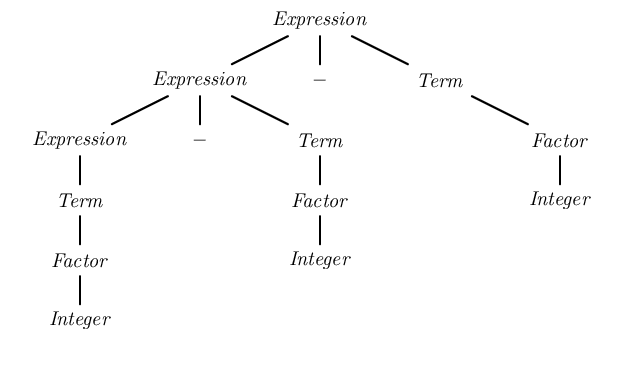 |
Left Recursion
In the formal language theory of computer science, left recursion is a special case of recursion where a string is recognized as part of a language by the fact that it decomposes into a string from that same language (on the left) and a suffix (on the right). For instance, 1+2+3 can be recognized as a sum because it can be broken into 1+2, also a sum, and +3, a suitable suffix. In terms of context-free grammar, a nonterminal is left-recursive if the leftmost symbol in one of its productions is itself (in the case of direct left recursion) or can be made itself by some sequence of substitutions (in the case of indirect left recursion). Definition A grammar is left-recursive if and only if there exists a nonterminal symbol A that can derive to a sentential form with itself as the leftmost symbol.. James Power, Department of Computer Science National University of Ireland, Maynooth Maynooth, Co. Kildare, Ireland. JPR02 Symbolically, : A \Rightarrow^+ A\alpha, where \Rightarrow^+ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Context-free Language
In formal language theory, a context-free language (CFL), also called a Chomsky type-2 language, is a language generated by a context-free grammar (CFG). Context-free languages have many applications in programming languages, in particular, most arithmetic expressions are generated by context-free grammars. Background Context-free grammar Different context-free grammars can generate the same context-free language. Intrinsic properties of the language can be distinguished from extrinsic properties of a particular grammar by comparing multiple grammars that describe the language. Automata The set of all context-free languages is identical to the set of languages accepted by pushdown automata, which makes these languages amenable to parsing. Further, for a given CFG, there is a direct way to produce a pushdown automaton for the grammar (and thereby the corresponding language), though going the other way (producing a grammar given an automaton) is not as direct. Examples An e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pushdown Automaton
In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack. Pushdown automata are used in theories about what can be computed by machines. They are more capable than finite-state machines but less capable than Turing machines (see below). Deterministic pushdown automata can recognize all deterministic context-free languages while nondeterministic ones can recognize all context-free languages, with the former often used in parser design. The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow access to and operations on deeper elements. Stack automata can recognize a strictly larger set of languages than pushdown automata. A nested stack automaton allows full access, and also allows stacked values to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Top-down Parsing
Top-down parsing in computer science is a parsing strategy where one first looks at the highest level of the parse tree and works down the parse tree by using the rewriting rules of a formal grammar. LL parsers are a type of parser that uses a top-down parsing strategy. Top-down parsing is a strategy of analyzing unknown data relationships by hypothesizing general parse tree structures and then considering whether the known fundamental structures are compatible with the hypothesis. It occurs in the analysis of both natural languages and computer languages. Top-down parsing can be viewed as an attempt to find left-most derivations of an input-stream by searching for parse-trees using a top-down expansion of the given formal grammar rules. Inclusive choice is used to accommodate ambiguity by expanding all alternative right-hand-sides of grammar rules. Simple implementations of top-down parsing do not terminate for left-recursive grammars, and top-down parsing with backtracking m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Backus–Naur Form
In computer science, Backus–Naur form (BNF, pronounced ), also known as Backus normal form, is a notation system for defining the Syntax (programming languages), syntax of Programming language, programming languages and other Formal language, formal languages, developed by John Backus and Peter Naur. It is a metasyntax for Context-free grammar, context-free grammars, providing a precise way to outline the rules of a language's structure. It has been widely used in official specifications, manuals, and textbooks on programming language theory, as well as to describe Document format, document formats, Instruction set, instruction sets, and Communication protocol, communication protocols. Over time, variations such as extended Backus–Naur form (EBNF) and augmented Backus–Naur form (ABNF) have emerged, building on the original framework with added features. Structure BNF specifications outline how symbols are combined to form syntactically valid sequences. Each BNF consists of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |