|
Good Quantum Number
In quantum mechanics, the eigenvalue q of an observable O is said to be a good quantum number if the observable O is a constant of motion. In other words, the quantum number is good if the corresponding observable commutes with the Hamiltonian. If the system starts from the eigenstate with an eigenvalue q, it remains on that state as the system evolves in time, and the measurement of O always yields the same eigenvalue q. Good quantum numbers are often used to label initial and final states in experiments. For example, in particle colliders: # Particles are initially prepared in approximate momentum eigenstates; the particle momentum being a good quantum number for non-interacting particles. # The particles are made to collide. At this point, the momentum of each particle is undergoing change and thus the particles’ momenta are not a good quantum number for the interacting particles during the collision. # A significant time after the collision, particles are measured in momentum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Factor
For any complex number written in polar form (such as ), the phase factor is the complex exponential (), where the variable is the ''phase'' of a wave or other periodic function. The phase factor is a unit complex number, i.e. a complex number of absolute value 1. It is commonly used in quantum mechanics and optics. It is a special case of ''phasors'', which may have arbitrary magnitude (i.e. not necessarily on the unit circle in the complex plane). Multiplying the equation of a plane wave by a phase factor shifts the phase of the wave by : e^ A\,e^ = A\,e^. In quantum mechanics, a phase factor is a complex coefficient that multiplies a ket , \psi\rangle or bra \langle\phi, . It does not, in itself, have any physical meaning, since the introduction of a phase factor does not change the expectation values of a Hermitian operator. That is, the values of \langle\phi, A , \phi\rangle and \langle\phi, A e^ , \phi\rangle are the same. However, ''differences'' in phas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ehrenfest Theorem
The Ehrenfest theorem, named after Austrian theoretical physicist Paul Ehrenfest, relates the time derivative of the expectation values of the position and momentum operators ''x'' and ''p'' to the expectation value of the force F=-V'(x) on a massive particle moving in a scalar potential V(x), The Ehrenfest theorem is a special case of a more general relation between the expectation of any quantum mechanical operator and the expectation of the commutator of that operator with the Hamiltonian of the system where is some quantum mechanical operator and is its expectation value. It is most apparent in the Heisenberg picture of quantum mechanics, where it amounts to just the expectation value of the Heisenberg equation of motion. It provides mathematical support to the correspondence principle. The reason is that Ehrenfest's theorem is closely related to Liouville's theorem of Hamiltonian mechanics, which involves the Poisson bracket instead of a commutator. Dirac's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
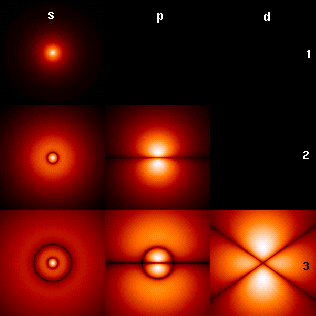
Quantum Number
In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence. Quantum numbers are closely related to eigenvalues of observables. When the corresponding observable commutes with the Hamiltonian of the system, the quantum number is said to be " good", and acts as a constant of motion in the quantum dynamics. History Electronic quantum numbers In the era of the old quantum theory, starting from Max Planck's proposal of quanta in his model of blackbody radiation (1900) and Albert Einstein's adaptation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Of Motion
In mechanics, a constant of motion is a physical quantity conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a ''mathematical'' constraint, the natural consequence of the equations of motion, rather than a ''physical'' constraint (which would require extra constraint forces). Common examples include energy, linear momentum, angular momentum and the Laplace–Runge–Lenz vector (for inverse-square force laws). Applications Constants of motion are useful because they allow properties of the motion to be derived without solving the equations of motion. In fortunate cases, even the trajectory of the motion can be derived as the intersection of isosurfaces corresponding to the constants of motion. For example, Poinsot's construction shows that the torque-free rotation of a rigid body is the intersection of a sphere (conservation of total angular momentum) and an ellipsoid (conservation of energy), a trajectory that might be otherw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary State
A stationary state is a quantum state with all observables independent of time. It is an eigenvector of the energy operator (instead of a quantum superposition of different energies). It is also called energy eigenvector, energy eigenstate, energy eigenfunction, or energy eigenket. It is very similar to the concept of atomic orbital and molecular orbital in chemistry, with some slight differences explained below. Introduction A stationary state is called ''stationary'' because the system remains in the same state as time elapses, in every observable way. For a single-particle Hamiltonian, this means that the particle has a constant probability distribution for its position, its velocity, its spin, etc. (This is true assuming the particle's environment is also static, i.e. the Hamiltonian is unchanging in time.) The wavefunction itself is not stationary: It continually changes its overall complex phase factor, so as to form a standing wave. The oscillation frequency of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Angular Momentum
In quantum mechanics, the total angular momentum quantum number parametrises the total angular momentum of a given particle, by combining its orbital angular momentum and its intrinsic angular momentum (i.e., its spin). If s is the particle's spin angular momentum and ℓ its orbital angular momentum vector, the total angular momentum j is \mathbf j = \mathbf s + \boldsymbol ~. The associated quantum number is the main total angular momentum quantum number ''j''. It can take the following range of values, jumping only in integer steps: \vert \ell - s\vert \le j \le \ell + s where ''ℓ'' is the azimuthal quantum number (parameterizing the orbital angular momentum) and ''s'' is the spin quantum number (parameterizing the spin). The relation between the total angular momentum vector j and the total angular momentum quantum number ''j'' is given by the usual relation (see angular momentum quantum number) \Vert \mathbf j \Vert = \sqrt \, \hbar The vector's ''z''-projection i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Set Of Commuting Observables
In quantum mechanics, a complete set of commuting observables (CSCO) is a set of commuting operators whose common eigenvectors can be used as a basis to express any quantum state. In the case of operators with discrete spectra, a CSCO is a set of commuting observables whose simultaneous eigenspaces span the Hilbert space and are linearly independent, so that the eigenvectors are uniquely specified by the corresponding sets of eigenvalues. In some simple cases, like bound state problems in one dimension, the energy spectrum is nondegenerate, and energy can be used to uniquely label the eigenstates. In more complicated problems, the energy spectrum is degenerate, and additional observables are needed to distinguish between the eigenstates. Since each pair of observables in the set commutes, the observables are all compatible so that the measurement of one observable has no effect on the result of measuring another observable in the set. It is therefore ''not'' necessary to specify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum Operator
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Being an observable, its eigenfunctions represent the distinguishable physical states of a system's angular momentum, and the corresponding eigenvalues the observable experimental values. When applied to a mathematical representation of the state of a system, yields the same state multiplied by its angular momentum value if the state is an eigenstate (as per the eigenstates/eigenvalues equation). In both classical and quantum mechanical systems, angular momentum (together with linear momentum and energy) is one of the three fundamental properties of motion.Introductory Quantum Mechanics, Richard L. Liboff, 2nd Edition, There are several angular momentum operators: total angular momentum (usually den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–orbit Interaction
In quantum mechanics, the spin–orbit interaction (also called spin–orbit effect or spin–orbit coupling) is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two effects: the apparent magnetic field seen from the electron perspective due to special relativity and the magnetic moment of the electron associated with its intrinsic spin due to quantum mechanics. For atoms, energy level splitting produced by the spin–orbit interaction is usually of the same order in size as the relativistic corrections to the kinetic energy and the zitterbewegung ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrogen Atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a single positively charged proton in the nucleus, and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe. In everyday life on Earth, isolated hydrogen atoms (called "atomic hydrogen") are extremely rare. Instead, a hydrogen atom tends to combine with other atoms in compounds, or with another hydrogen atom to form ordinary (diatomic) hydrogen gas, H2. "Atomic hydrogen" and "hydrogen atom" in ordinary English use have overlapping, yet distinct, meanings. For example, a water molecule contains two hydrogen atoms, but does not contain atomic hydrogen (which would refer to isolated hydrogen atoms). Atomic spectroscopy shows that there is a discrete infinite set of states in which a hydrogen (or any) atom can exist, contrary to the predictions of classical physics. At ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |