|
Generalized Lotka–Volterra Equation
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator–prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food webs. However, they lack features of other ecological models such as predator preference and nonlinear functional responses, and they cannot be used to model mutualism without allowing indefinite population growth. The generalised Lotka-Volterra equations model the dynamics of the populations x_1, x_2, \dots of n biological species. Together, these populations can be considered as a vector \mathbf. They are a set of ordinary differential equations given by : \frac = x_i f_i(\mathbf), where the vector \mathbf is given by : \mathbf = \mathbf + A\mathbf, where \mathbf is a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trophic Network
A food web is the natural interconnection of food chains and a graphical representation of what-eats-what in an ecological community. Another name for food web is consumer-resource system. Ecologists can broadly lump all life forms into one of two categories called trophic levels: 1) the autotrophs, and 2) the heterotrophs. To maintain their bodies, grow, develop, and to reproduce, autotrophs produce organic matter from inorganic substances, including both minerals and gases such as carbon dioxide. These chemical reactions require energy, which mainly comes from the Sun and largely by photosynthesis, although a very small amount comes from bioelectrogenesis in wetlands, and mineral electron donors in hydrothermal vents and hot springs. These trophic levels are not binary, but form a gradient that includes complete autotrophs, which obtain their sole source of carbon from the atmosphere, mixotrophs (such as carnivorous plants), which are autotrophic organisms t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Immanuel Bomze
Immanuel Bomze is an Austrian mathematician. In his Ph.D. thesis, he completely classified all (more than 100 topologically different) possible flows of the generalized Lotka–Volterra dynamics ( generalized Lotka–Volterra equation) on the plane, employing equivalence of this dynamics to the 3-type replicator equation. In “Non-cooperative two-person games in biology: a classification” (1986) and his book jointly authored with B. M. Pötscher (''Game theoretic foundations of evolutionary stability'', Springer 1989), he popularized the field of evolutionary game theory which at that time received most attention within Theoretical Biology, among researchers in Economics and Social Sciences. Around the turn of the millennium, he coined, together with his co-authors, the now widely used terms "Standard Quadratic Optimization" and "Copositive Optimization" or "Copositive Programming". While the further deals with the simplest problem class in non-linear optimization with an NP-ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in French an ''équation'' is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation. ''Solving'' an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables. An equation is written as two expressions, connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volterra Lattice
In mathematics, the Volterra lattice, also known as the discrete KdV equation, the Kac–van Moerbeke lattice, and the Langmuir lattice, is a system of ordinary differential equations with variables indexed by some of the points of a 1-dimensional lattice. It was introduced by and and is named after Vito Volterra. The Volterra lattice is a special case of the generalized Lotka–Volterra equation describing predator–prey interactions, for a sequence of species with each species preying on the next in the sequence. The Volterra lattice also behaves like a discrete version of the KdV equation. The Volterra lattice is an integrable system, and is related to the Toda lattice The Toda lattice, introduced by , is a simple model for a one-dimensional crystal in solid state physics Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and .... It is also used as a model for Langmuir waves in plas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Replicator Equation
In mathematics, the replicator equation is a deterministic monotone non-linear and non-innovative game dynamic used in evolutionary game theory. The replicator equation differs from other equations used to model replication, such as the quasispecies equation, in that it allows the fitness function to incorporate the distribution of the population types rather than setting the fitness of a particular type constant. This important property allows the replicator equation to capture the essence of selection. Unlike the quasispecies equation, the replicator equation does not incorporate mutation and so is not able to innovate new types or pure strategies. Equation The most general continuous form of the replicator equation is given by the differential equation: : \dot = x_i f_i(x) - \phi(x) \quad \phi(x) = \sum_^ where x_i is the proportion of type i in the population, x=(x_1, \ldots, x_n) is the vector of the distribution of types in the population, f_i(x) is the fitness of type ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Community Matrix
In mathematical biology, the community matrix is the linearization of the Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point. The Lotka–Volterra predator–prey model is : \begin \dfrac &=& x(\alpha - \beta y) \\ \dfrac &=& - y(\gamma - \delta x), \end where ''x''(''t'') denotes the number of prey, ''y''(''t'') the number of predators, and ''α'', ''β'', ''γ'' and ''δ'' are constants. By the Hartman–Grobman theorem the non-linear system is topologically equivalent to a linearization of the system about an equilibrium point (''x''*, ''y''*), which has the form : \begin \frac \\ \frac \end = \mathbf \begin u \\ v \end, where ''u'' = ''x'' − ''x''* and ''v'' = ''y'' − ''y''*. In mathematical biology, the Jacobian matrix \mathbf evaluated at the equilibrium point (''x''*, ''y''*) is called the community matrix. By the stable manifold theorem, if one or both eigenvalues of \mathbf ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Competitive Lotka–Volterra Equations
The competitive Lotka–Volterra equations are a simple model of the population dynamics of species competing for some common resource. They can be further generalised to the Generalized Lotka–Volterra equation to include trophic interactions. Overview The form is similar to the Lotka–Volterra equations for predation in that the equation for each species has one term for self-interaction and one term for the interaction with other species. In the equations for predation, the base population model is exponential. For the competition equations, the logistic equation is the basis. The logistic population model, when used by ecologists often takes the following form: = rx\left(1-\right). Here is the size of the population at a given time, is inherent per-capita growth rate, and is the carrying capacity. Two species Given two populations, and , with logistic dynamics, the Lotka–Volterra formulation adds an additional term to account for the species' interactions. Thu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
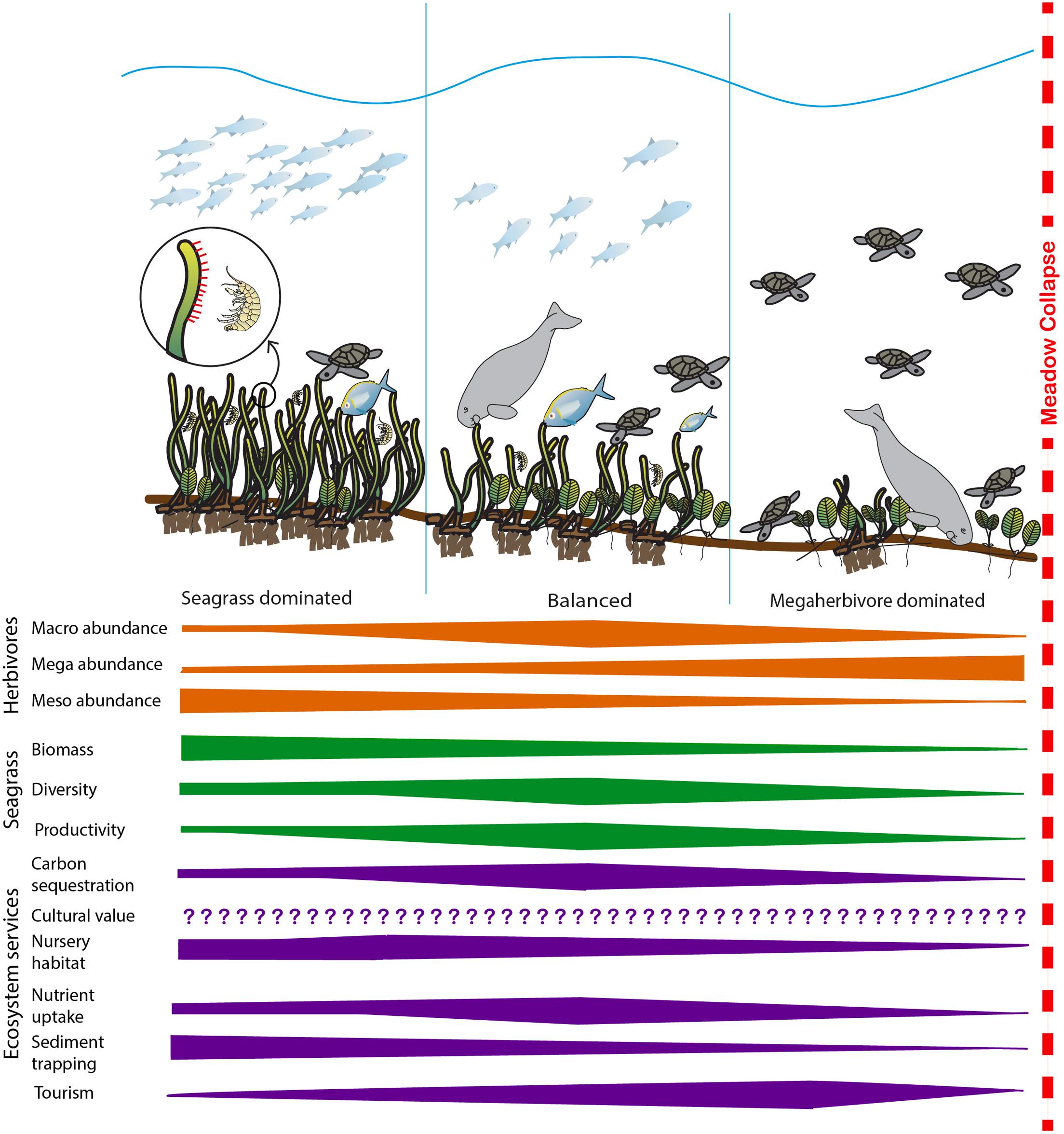
Species Abundance
In ecology, local abundance is the relative representation of a species in a particular ecosystem. It is usually measured as the number of individuals found per sample. The ratio of abundance of one species to one or multiple other species living in an ecosystem is referred to as relative species abundances. Both indicators are relevant for computing biodiversity. A variety of sampling methods are used to measure abundance. For larger animals, these may include spotlight counts, track counts and roadkill counts, as well as presence at monitoring stations. In many plant communities the abundances of plant species are measured by plant cover, i.e. the relative area covered by different plant species in a small plot. Abundance is in simplest terms usually measured by identifying and counting every individual of every species in a given sector. It is common for the distribution of species to be skewed so that a few species take up the bulk of individuals collected. Relative spec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barro Colorado Island Research Station
The Smithsonian Tropical Research Institute (STRI, es, Instituto Smithsonian de Investigaciones Tropicales) is located in Panama and is the only bureau of the Smithsonian Institution based outside of the United States. It is dedicated to understanding the past, present, and future of tropical ecosystems and their relevance to human welfare. STRI grew out of a small field station established in 1923 on Barro Colorado Island in the Panama Canal Zone to become one of the world's leading tropical research organizations. STRI's facilities provide for long-term ecological studies in the tropics and are used by some 1,200 visiting scientists from academic and research institutions around the world every year. History Smithsonian scientists first came to Panama during the construction of the Panama Canal from 1904 to 1914. The Secretary of the Smithsonian Institution, Charles Doolittle Walcott, reached an agreement with Federico Boyd to conduct a biological inventory of the new Canal Zo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principle Of Maximum Entropy
The principle of maximum entropy states that the probability distribution which best represents the current state of knowledge about a system is the one with largest entropy, in the context of precisely stated prior data (such as a proposition that expresses testable information). Another way of stating this: Take precisely stated prior data or testable information about a probability distribution function. Consider the set of all trial probability distributions that would encode the prior data. According to this principle, the distribution with maximal information entropy is the best choice. History The principle was first expounded by E. T. Jaynes in two papers in 1957 where he emphasized a natural correspondence between statistical mechanics and information theory. In particular, Jaynes offered a new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy of statistical mechanics and the information entropy of informa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carrying Capacity
The carrying capacity of an environment is the maximum population size of a biological species that can be sustained by that specific environment, given the food, habitat, water, and other resources available. The carrying capacity is defined as the environment's maximal load, which in population ecology corresponds to the population equilibrium, when the number of deaths in a population equals the number of births (as well as immigration and emigration). The effect of carrying capacity on population dynamics is modelled with a logistic function. Carrying capacity is applied to the maximum population an environment can support in ecology, agriculture and fisheries. The term carrying capacity has been applied to a few different processes in the past before finally being applied to population limits in the 1950s. The notion of carrying capacity for humans is covered by the notion of sustainable population. At the global scale, scientific data indicates that humans are living beyond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |