|
Gap Theorem
:''See also Gap theorem (other) for other gap theorems in mathematics.'' In computational complexity theory, the Gap Theorem, also known as the Borodin–Trakhtenbrot Gap Theorem, is a major theorem about the complexity of computable functions. It essentially states that there are arbitrarily large computable gaps in the hierarchy of complexity classes. For any computable function that represents an increase in computational resources, one can find a resource bound such that the set of functions computable within the expanded resource bound is the same as the set computable within the original bound. The theorem was proved independently by Boris Trakhtenbrot and Allan Borodin. Although Trakhtenbrot's derivation preceded Borodin's by several years, it was not known nor recognized in the West until after Borodin's work was published. Gap theorem The general form of the theorem is as follows. :Suppose is an abstract (Blum) complexity measure. For any total computable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gap Theorem (other)
{{mathematical disambiguation ...
In mathematics, gap theorem may refer to: * The Weierstrass gap theorem in algebraic geometry * The Ostrowski–Hadamard gap theorem on lacunary function * The Fabry gap theorem on lacunary functions * The ''gap theorem'' of Fourier analysis, a statement about the vanishing of discrete Fourier coefficients for functions that are identically zero on an interval shorter than 2π * The gap theorem in computational complexity theory * Saharon Shelah's Main Gap Theorem which solved Morley's problem in model theory In mathematical logic, model theory is the study of the relationship between formal theories (a collection of sentences in a formal language expressing statements about a mathematical structure), and their models (those structures in which the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
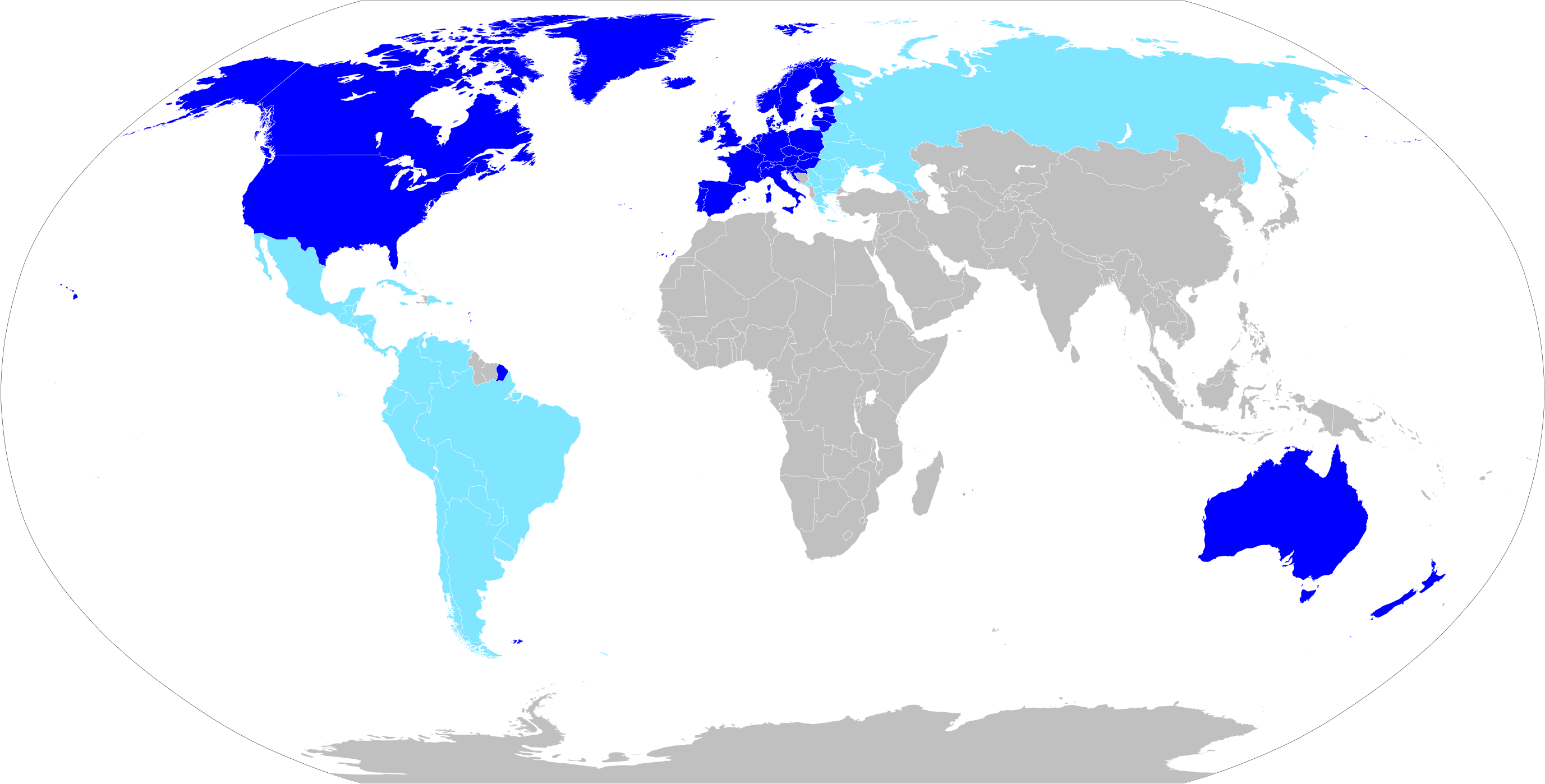
Western World
The Western world, also known as the West, primarily refers to the various nations and states in the regions of Europe, North America, and Oceania.Western Civilization Our Tradition; James Kurth; accessed 30 August 2011 The Western world is also known as the Occident (from the word ''occidēns'' "setting down, sunset, west") in contrast to the Eastern world known as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Hierarchy Theorem
In computational complexity theory, the space hierarchy theorems are separation results that show that both deterministic and nondeterministic machines can solve more problems in (asymptotically) more space, subject to certain conditions. For example, a deterministic Turing machine can solve more decision problems in space ''n'' log ''n'' than in space ''n''. The somewhat weaker analogous theorems for time are the time hierarchy theorems. The foundation for the hierarchy theorems lies in the intuition that with either more time or more space comes the ability to compute more functions (or decide more languages). The hierarchy theorems are used to demonstrate that the time and space complexity classes form a hierarchy where classes with tighter bounds contain fewer languages than those with more relaxed bounds. Here we define and prove the space hierarchy theorem. The space hierarchy theorems rely on the concept of space-constructible functions. The deterministic and nondeterminist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Hierarchy Theorem
In computational complexity theory, the time hierarchy theorems are important statements about time-bounded computation on Turing machines. Informally, these theorems say that given more time, a Turing machine can solve more problems. For example, there are problems that can be solved with ''n''2 time but not ''n'' time. The time hierarchy theorem for deterministic multi-tape Turing machines was first proven by Richard E. Stearns and Juris Hartmanis in 1965. It was improved a year later when F. C. Hennie and Richard E. Stearns improved the efficiency of the Universal Turing machine. Consequent to the theorem, for every deterministic time-bounded complexity class, there is a strictly larger time-bounded complexity class, and so the time-bounded hierarchy of complexity classes does not completely collapse. More precisely, the time hierarchy theorem for deterministic Turing machines states that for all time-constructible functions ''f''(''n''), :\mathsf\left(o\left(\frac\right)\rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constructible Function
In complexity theory, a time-constructible function is a function ''f'' from natural numbers to natural numbers with the property that ''f''(''n'') can be constructed from ''n'' by a Turing machine in the time of order ''f''(''n''). The purpose of such a definition is to exclude functions that do not provide an upper bound on the runtime of some Turing machine. Time-constructible definitions There are two different definitions of a time-constructible function. In the first definition, a function ''f'' is called time-constructible if there exists a positive integer ''n''0 and Turing machine ''M'' which, given a string 1''n'' consisting of ''n'' ones, stops after exactly ''f''(''n'') steps for all ''n'' ≥ ''n''0. In the second definition, a function ''f'' is called time-constructible if there exists a Turing machine ''M'' which, given a string 1''n'', outputs the binary representation of ''f''(''n'') in '' O''(''f''(''n'')) time (a unary representation may be used instead, since the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Model
A computational model uses computer programs to simulate and study complex systems using an algorithmic or mechanistic approach and is widely used in a diverse range of fields spanning from physics, chemistry and biology to economics, psychology, cognitive science and computer science. The system under study is often a complex nonlinear system for which simple, intuitive analytical solutions are not readily available. Rather than deriving a mathematical analytical solution to the problem, experimentation with the model is done by adjusting the parameters of the system in the computer, and studying the differences in the outcome of the experiments. Operation theories of the model can be derived/deduced from these computational experiments. Examples of common computational models are weather forecasting models, earth simulator models, flight simulator models, molecular protein folding models, and neural network models. See also * Computational cognition *Reversible computing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Computable Function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithms, in the sense that a function is computable if there exists an algorithm that can do the job of the function, i.e. given an input of the function domain it can return the corresponding output. Computable functions are used to discuss computability without referring to any concrete model of computation such as Turing machines or register machines. Any definition, however, must make reference to some specific model of computation but all valid definitions yield the same class of functions. Particular models of computability that give rise to the set of computable functions are the Turing-computable functions and the general recursive functions. Before the precise definition of computable function, mathematicians often used the informal term ''effectively calculable''. This term has since come to be identified with the com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blum Axioms
In computational complexity theory the Blum axioms or Blum complexity axioms are axioms that specify desirable properties of complexity measures on the set of computable functions. The axioms were first defined by Manuel Blum in 1967. Importantly, Blum's speedup theorem and the Gap theorem hold for any complexity measure satisfying these axioms. The most well-known measures satisfying these axioms are those of time (i.e., running time) and space (i.e., memory usage). Definitions A Blum complexity measure is a pair (\varphi, \Phi) with \varphi a numbering of the partial computable functions \mathbf^ and a computable function :\Phi: \mathbb \to \mathbf^ which satisfies the following Blum axioms. We write \varphi_i for the ''i''-th partial computable function under the Gödel numbering \varphi, and \Phi_i for the partial computable function \Phi(i). * the domains of \varphi_i and \Phi_i are identical. * the set \ is recursive. Examples * (\varphi, \Phi) is a complexity mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The ACM
The ''Journal of the ACM'' is a peer-reviewed scientific journal covering computer science in general, especially theoretical aspects. It is an official journal of the Association for Computing Machinery. Its current editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The highest-ranking editor of a publication may also be titled editor, managing ... is Venkatesan Guruswami. The journal was established in 1954 and "computer scientists universally hold the ''Journal of the ACM'' in high esteem". See also * '' Communications of the ACM'' References External links * Publications established in 1954 Computer science journals Association for Computing Machinery academic journals Bimonthly journals English-language journals {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allan Borodin
Allan Bertram Borodin (born 1941) is a Canadian-American computer scientist who is a professor at the University of Toronto.Borodin named University Professor , U. Toronto Computer Science, retrieved 2012-03-17.Past prizes and awards PIMS, retrieved 2012-03-17. Biography Borodin did his undergraduate studies at , earning a bachelor's degree in mathematics in 1963. After earning a master's degree at the |
Boris Trakhtenbrot
Boris (Boaz) Abramovich Trakhtenbrot (russian: Борис Авраамович Трахтенброт, he, בועז טרכטנברוט; 19 February 1921 – 19 September 2016) was a Russian-Israeli mathematician in logic, algorithms, theory of computation, and cybernetics. Biography Trakhtenbrot was born in Brichevo, northern Bessarabia (now Tîrnova, Moldova). He studied at the Moldovan State Pedagogical Institute in Kishinev, Chernivtsi University, and the Ukrainian Academy of Science's Mathematical Institute, completing a Ph.D. at the latter institution in 1950. He worked at Akademgorodok, Novosibirsk during the 1960s and 1970s. In 1964 Trakhtenbrot discovered and proved a fundamental result in theoretical computer science called the gap theorem. He also discovered and proved the theorem in logic, model theory, and computability theory now known as Trakhtenbrot's theorem. After immigrating to Israel in 1981, he became a professor in the Faculty of Exact Sciences at Te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |