|
G. I. Taylor
Sir Geoffrey Ingram Taylor Order of Merit, OM Royal Society of London, FRS FRSE (7 March 1886 – 27 June 1975) was a British physicist and mathematician, who made contributions to fluid dynamics and wave theory. Early life and education Taylor was born in St. John's Wood, London. His father, Edward Ingram Taylor, was an artist, and his mother, Margaret Boole, came from a family of mathematicians (his aunt was Alicia Boole Stott and his grandfather was George Boole). As a child he was fascinated by science after attending the Royal Institution Christmas Lectures, and performed experiments using paint rollers and sticky-tape. Taylor read mathematics and physics at Trinity College, Cambridge from 1905 to 1908. He won several scholarships and prizes at Cambridge, one of which enabled him to study under J. J. Thomson. Career and research Taylor published his first paper while he was still an undergraduate. In it, he showed that Double-slit experiment, interference of visible ligh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Middlesex
Middlesex (; abbreviation: Middx) is a Historic counties of England, former county in South East England, now mainly within Greater London. Its boundaries largely followed three rivers: the River Thames, Thames in the south, the River Lea, Lea to the east and the River Colne, Hertfordshire, Colne to the west. A line of hills formed its northern boundary with Hertfordshire. The county was the List of counties of England by area in 1831, second smallest of the historic counties of England, after Rutland. The name of the county derives from its origin as a homeland for the Middle Saxons in the early Middle Ages, with the county subsequently part of that territory in the ninth or tenth century. The City of London, formerly part of the county, became a self governing county corporate in the twelfth century; the City was still able to exert influence as the sheriffs of London maintained their jurisdiction in Middlesex, though the county otherwise remained separate. To the east of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Dispersion
Taylor dispersion or Taylor diffusion is an apparent or effective diffusion of some scalar field arising on the large scale due to the presence of a strong, confined, zero-mean shear flow on the small scale. Essentially, the shear acts to smear out the concentration distribution in the direction of the flow, enhancing the rate at which it spreads in that direction. The effect is named after the British fluid dynamicist G. I. Taylor, who described the shear-induced dispersion for large Peclet numbers. The analysis was later generalized by Rutherford Aris for arbitrary values of the Peclet number, and hence the process is sometimes also referred to as Taylor-Aris dispersion. The canonical example is that of a simple diffusing species in uniform Poiseuille flow through a uniform circular pipe with no-flux boundary conditions, but is relevant in many other contexts, including the spread of pollutants in rivers and of drugs in blood flow and rivulet flow. Description We use ''z'' as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Scraping Flow
In fluid dynamics, Taylor scraping flow is a type of two-dimensional corner flow occurring when one of the wall is sliding over the other with constant velocity, named after G. I. Taylor. Flow description Consider a plane wall located at \theta=0 in the cylindrical coordinates (r,\theta), moving with a constant velocity U towards the left. Consider another plane wall(scraper), at an inclined position, making an angle \alpha from the positive x direction and let the point of intersection be at r=0. This description is equivalent to moving the scraper towards right with velocity U. The problem is singular at r=0 because at the origin, the velocities are discontinuous, thus the velocity gradient is infinite there. Taylor noticed that the inertial terms are negligible as long as the region of interest is within r\ll\nu/U( or, equivalently Reynolds number Re = Ur/\nu \ll 1), thus within the region the flow is essentially a Stokes flow. For example, George Batchelor gives a typical val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Number
In fluid dynamics, the Taylor number (Ta) is a dimensionless quantity that characterizes the importance of centrifugal "forces" or so-called inertial forces due to rotation of a fluid about an axis, relative to viscous forces. In 1923 Geoffrey Ingram Taylor introduced this quantity in his article on the stability of flow. The typical context of the Taylor number is in characterization of the Couette flow between rotating colinear cylinders or rotating concentric spheres. In the case of a system which is not rotating uniformly, such as the case of cylindrical Couette flow, where the outer cylinder is stationary and the inner cylinder is rotating, inertial forces will often tend to destabilize a system, whereas viscous forces tend to stabilize a system and damp out perturbations and turbulence. On the other hand, in other cases the effect of rotation can be stabilizing. For example, in the case of cylindrical Couette flow with positive Rayleigh discriminant, there are no axisymme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor–Proudman Theorem
In fluid mechanics, the Taylor–Proudman theorem (after Geoffrey Ingram Taylor and Joseph Proudman) states that when a solid body is moved slowly within a fluid that is steadily rotated with a high angular velocity \Omega, the fluid velocity will be uniform along any line parallel to the axis of rotation. \Omega must be large compared to the movement of the solid body in order to make the Coriolis force large compared to the acceleration terms. Derivation The Navier–Stokes equations for steady flow, with zero viscosity and a body force corresponding to the Coriolis force, are : \rho(\cdot\nabla)=-\nabla p, where is the fluid velocity, \rho is the fluid density, and p the pressure. If we assume that F=\nabla\Phi=-2\rho\mathbf\Omega\times is a scalar potential and the advective term on the left may be neglected (reasonable if the Rossby number is much less than unity) and that the flow is incompressible (density is constant), the equations become: : 2\rho\mathbf\Omega\times=- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
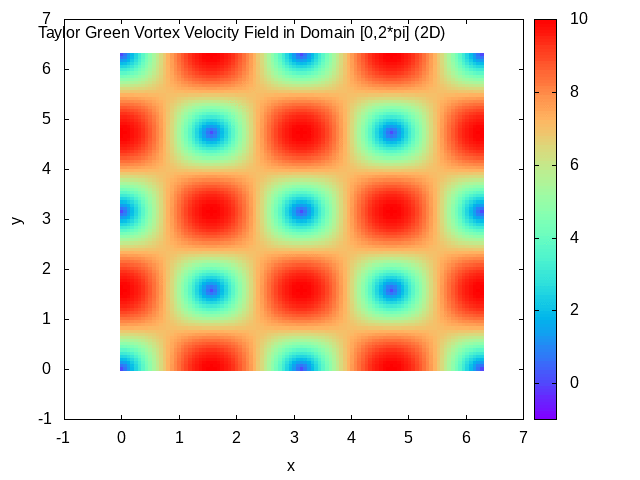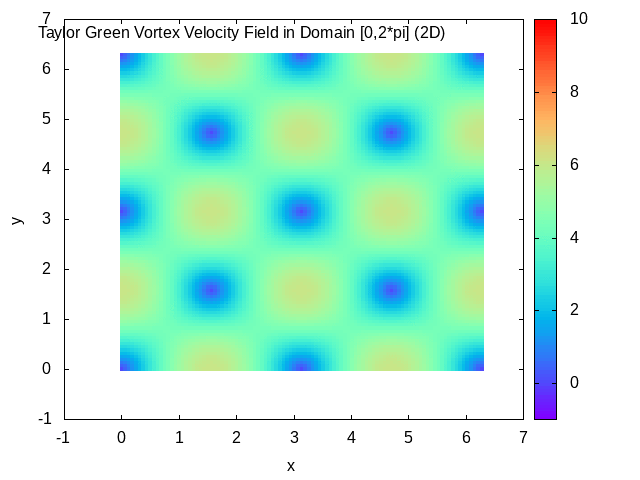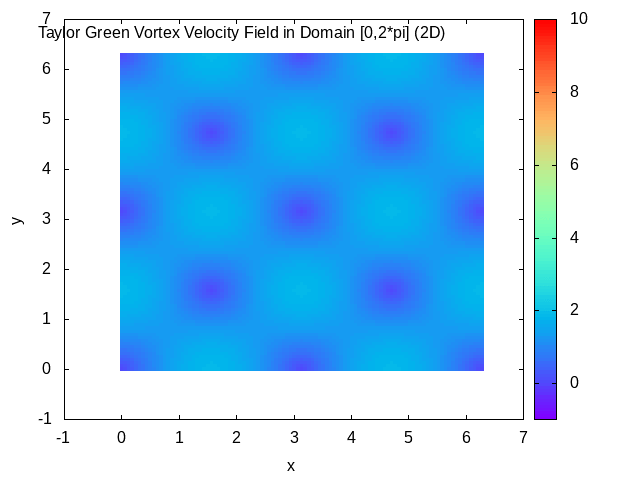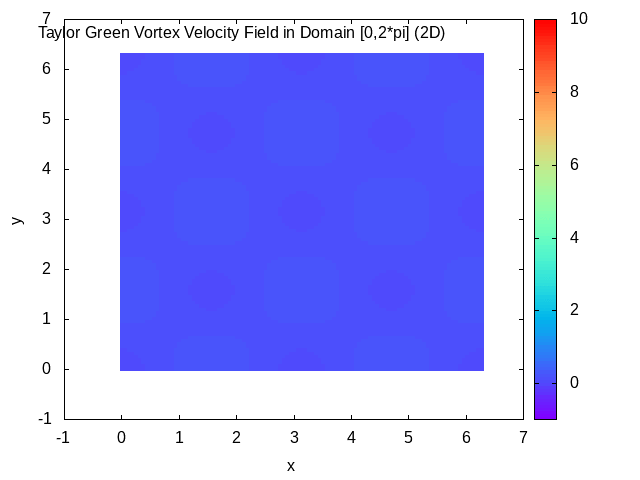
Taylor–Green Vortex
In fluid dynamics, the Taylor–Green vortex is an unsteady flow of a decaying vortex, which has an exact closed form solution of the incompressible Navier–Stokes equations in Cartesian coordinates. It is named after the British physicist and mathematician Geoffrey Ingram Taylor and his collaborator A. E. Green. Taylor, G. I. and Green, A. E., ''Mechanism of the Production of Small Eddies from Large Ones'', Proc. R. Soc. Lond. A, 158, 499–521 (1937). Original work In the original work of Taylor and Green, a particular flow is analyzed in three spatial dimensions, with the three velocity components \mathbf=(u,v,w) at time t=0 specified by : u = A \cos ax \sin by \sin cz, : v = B \sin ax \cos by \sin cz, : w = C \sin ax \sin by \cos cz. The continuity equation \nabla \cdot \mathbf=0 determines that Aa+Bb+Cc=0. The small time behavior of the flow is then found through simplification of the incompressible Navier–Stokes equations using the initial flow to give a ste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor–Culick Flow
In fluid dynamics, Taylor–Culick flow describes the axisymmetric flow inside a long slender cylinder with one end closed, supplied by a constant flow injection through the sidewall. The flow is named after Geoffrey Ingram Taylor and F. E. C. Culick. In 1956, Taylor showed that when a fluid forced into porous sheet of cone or wedge, a favorable longitudinal pressure gradient is set up in the direction of the flow inside the cone or wedge and the flow is rotational; this is in contrast in the vice versa case wherein the fluid is forced out of the cone or wedge sheet from inside in which case, the flow is uniform inside the cone or wedge and is obviously potential. Taylor also obtained solutions for the velocity in the limiting case where the cone or the wedge degenerates into a circular tube or parallel plates. Later in 1966, Culick found the solution corresponding to the tube problem, in problem applied to solid-propellant rocket combustion. Here the thermal expansion of the gas due ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor–Maccoll Flow
Taylor–Maccoll flow refers to the steady flow behind a conical shock wave that is attached to a solid cone. The flow is named after G. I. Taylor and J. W. Maccoll, whom described the flow in 1933, guided by an earlier work of Theodore von Kármán.Von Karman, T., & Moore, N. B. (1932). Resistance of slender bodies moving with supersonic velocities, with special reference to projectiles. Transactions of the American Society of Mechanical Engineers, 54(2), 303-310.Maccoll, J. W. (1937). The conical shock wave formed by a cone moving at a high speed. Proceedings of the Royal Society of London. Series A-Mathematical and Physical Sciences, 159(898), 459-472. Mathematical description Consider a steady supersonic flow past a solid cone that has a semi-vertical angle \chi. A conical shock wave can form in this situation, with the vertex of the shock wave lying at the vertex of the solid cone. If it were a two-dimensional problem, i.e., for a supersonic flow past a wedge, then the incom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeldovich–Taylor Flow
Zeldovich–Taylor flow (also known as Zeldovich–Taylor expansion wave) is the fluid motion of gaseous detonation products behind Chapman–Jouguet detonation wave. The flow was described independently by Yakov Zeldovich in 1942 and G. I. Taylor in 1950, although G. I. Taylor carried out the work in 1941 that being circulated in the British Ministry of Home Security. Since naturally occurring detonation waves are in general a Chapman–Jouguet detonation wave, the solution becomes very useful in describing real-life detonation waves. Mathematical description Consider a spherically outgoing Chapman–Jouguet detonation wave propagating with a constant velocity D. By definition, immediately behind the detonation wave, the gas velocity is equal to the local sound speed c with respect to the wave. Let v(r,t) be the radial velocity of the gas behind the wave, in a fixed frame. The detonation is ignited at t=0 at r=0. For t>0, the gas velocity must be zero at the center r=0 and sh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Cone
A Taylor cone refers to the cone observed in electrospinning, electrospraying and hydrodynamic spray processes from which a jet of charged particles emanates above a threshold voltage. Aside from electrospray ionization in mass spectrometry, the Taylor cone is important in field-emission electric propulsion (FEEP) and colloid thrusters used in fine control and high efficiency (low power) thrust of spacecraft. History This cone was described by Sir Geoffrey Ingram Taylor in 1964 before electrospray was "discovered". This work followed on the work of Zeleny who photographed a cone-jet of glycerine in a strong electric field and the work of several others: Wilson and Taylor (1925), Nolan (1926) and Macky (1931). Taylor was primarily interested in the behavior of water droplets in strong electric fields, such as in thunderstorms. Formation When a small volume of electrically conductive liquid is exposed to an electric field, the shape of liquid starts to deform from the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dislocation
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to slide over each other at low stress levels and is known as ''glide'' or Slip (materials science), slip. The crystalline order is restored on either side of a ''glide dislocation'' but the atoms on one side have moved by one position. The crystalline order is not fully restored with a ''partial dislocation''. A dislocation defines the boundary between ''slipped'' and ''unslipped'' regions of material and as a result, must either form a complete loop, intersect other dislocations or defects, or extend to the edges of the crystal. A dislocation can be characterised by the distance and direction of movement it causes to atoms which is defined by the Burgers vector. Plasticity (physics), Plastic deformation of a material occurs by the creation and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Microscale
In fluid dynamics, the Taylor microscale, which is sometimes called the turbulence length scale, is a length scale used to characterize a turbulent fluid flow. This microscale is named after Geoffrey Ingram Taylor. The Taylor microscale is the intermediate length scale at which fluid viscosity significantly affects the dynamics of turbulent eddies in the flow. This length scale is traditionally applied to turbulent flow which can be characterized by a Kolmogorov spectrum of velocity fluctuations. In such a flow, length scales which are larger than the Taylor microscale are not strongly affected by viscosity. These larger length scales in the flow are generally referred to as the inertial range. Below the Taylor microscale the turbulent motions are subject to strong viscous forces and kinetic energy is dissipated into heat. These shorter length scale motions are generally termed the dissipation range. Calculation of the Taylor microscale is not entirely straightforward, requi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |