|
Furuta Pendulum
The Furuta pendulum, or rotational inverted pendulum, consists of a driven arm which rotates in the horizontal plane and a pendulum attached to that arm which is free to rotate in the vertical plane. It was invented in 1992 at Tokyo Institute of Technology by Katsuhisa FurutaXu, Y., Iwase, M. and Furuta, K. (2001) “Time optimal swing-up control of single pendulum”, Journal of Dynamic Systems, Measurement, and Control, 123(3), 518-527.Furuta, K., Iwase, M. (2004) “Swing-up time analysis of pendulum”, Bulletin of the Polish Academy of Sciences: Technical Sciences, 52(3), 153-163.Iwase, M., Åström, K.J., Furuta, K. and Åkesson, J. (2006) “Analysis of safe manual control by using Furuta pendulum”, Proceedings of the IEEE International Conference on Control Applications, 568-572. and his colleagues. It is an example of a complex nonlinear oscillator of interest in control system theory. The pendulum is underactuated and extremely non-linear due to the gravitational fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Adelaide
The University of Adelaide is a public university, public research university based in Adelaide, South Australia. Established in 1874, it is the third-oldest university in Australia. Its main campus in the Adelaide city centre includes many Sandstone universities, sandstone buildings of historical and architectural significance, such as Bonython Hall. Its royal charter awarded by Queen Victoria in 1881 allowed it to become the University of London, second university in the English-speaking world to confer degrees to women. It Adelaide University, plans to merge with the neighbouring University of South Australia, is adjacent to the Australian Space Agency headquarters on Lot Fourteen and is part of the Adelaide BioMed City research precinct. The university was founded at the former South Australian Society of Arts, Royal South Australian Society of Arts by the Union College and studies were initially conducted at its State Library of South Australia, Institute Building. The soc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-balancing Unicycle
An electric unicycle (often initialized as EUC or acronymized yuke or Uni) is a self-balancing personal transporter with a unicycle, single wheel. The rider controls speed by leaning forwards or backwards, and steers by twisting or tilting the unit side to side. The self-balancing mechanism uses accelerometers and gyroscopes. Most manufacturers of EUCs are based out of China, including Segway, Inmotion, Kingsong, Begode, and Leaperkim. Operation Similar to Self-balancing scooter, hoverboards, Onewheels, and Segways, electric unicycles are self-balancing in a forward and backward direction, with side-to-side (lateral) stability being provided by human steering motions that tilt or twist the unit, similar to Bicycle and motorcycle dynamics. The control of a unicycle can be considered to be similar to an inverted pendulum. Many electric unicycles have suspension, either operated by air or springs. Electric unicycles come in varying speeds, battery capacities, and motor wattages. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertia Wheel Pendulum
An inertia wheel pendulum is a pendulum with an inertia wheel attached. It can be used as a pedagogical problem in control theory. This type of pendulum is often confused with the gyroscopic effect, which has completely different physical nature. See also * Inverted pendulum * Robotic unicycle * Spinning top A spinning top, or simply a top, is a toy with a squat body and a sharp point at the bottom, designed to be rotation, spun on its vertical Axis of rotation, axis, balancing on the tip due to the gyroscopic effect. Once set in motion, a top will ... References * Mark W. Spong, Peter Corke, Rogelio Lozano. Nonlinear Control of the Gyroscopic Pendulum'' Pendulums Control engineering {{classicalmechanics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double Inverted Pendulum
A double inverted pendulum is the combination of the inverted pendulum and the double pendulum. The double inverted pendulum is unstable, meaning that it will fall down unless it is controlled in some way. The two main methods of controlling a double inverted pendulum are moving the base, as with the inverted pendulum, or by applying a torque at the pivot point between the two pendulums. See also *Inverted pendulum *Inertia wheel pendulum *Furuta pendulum *Tuned mass damper A tuned mass damper (TMD), also known as a harmonic absorber or seismic damper, is a device mounted in structures to reduce mechanical vibrations, consisting of a mass mounted on one or more damped springs. Its oscillation frequency is tune ... References External links A dynamical simulation of a double inverted pendulum on an oscillatory base Pendulums Control engineering {{classicalmechanics-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverted Pendulum
An inverted pendulum is a pendulum that has its center of mass above its Lever, pivot point. It is unstable equilibrium, unstable and falls over without additional help. It can be suspended stably in this inverted position by using a control system to monitor the angle of the pole and move the pivot point horizontally back under the center of mass when it starts to fall over, keeping it balanced. The inverted pendulum is a classic problem in dynamics (mechanics), dynamics and control theory and is used as a benchmark for testing control strategies. It is often implemented with the pivot point mounted on a cart that can move horizontally under control of an electronic servo system as shown in the photo; this is called a cart and pole apparatus. Most applications limit the pendulum to 1 Degrees of freedom (mechanics), degree of freedom by affixing the pole to an axis of rotation. Whereas a normal pendulum is stable when hanging downward, an inverted pendulum is inherently unstab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
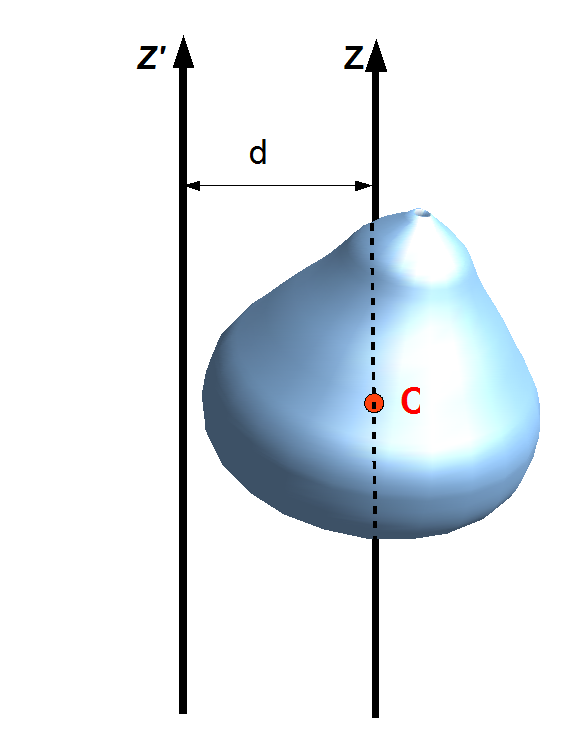
Parallel Axis Theorem
The parallel axis theorem, also known as Huygens–Steiner theorem, or just as Steiner's theorem, named after Christiaan Huygens and Jakob Steiner, can be used to determine the moment of inertia or the second moment of area of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's center of gravity and the perpendicular distance between the axes. Mass moment of inertia Suppose a body of mass is rotated about an axis passing through the body's center of mass. The body has a moment of inertia with respect to this axis. The parallel axis theorem states that if the body is made to rotate instead about a new axis , which is parallel to the first axis and displaced from it by a distance , then the moment of inertia with respect to the new axis is related to by : I = I_\mathrm + md^2. Explicitly, is the perpendicular distance between the axes and . The parallel axis theorem can be applied with the stretch rule and perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Furuta Pendulum
The Furuta pendulum, or rotational inverted pendulum, consists of a driven arm which rotates in the horizontal plane and a pendulum attached to that arm which is free to rotate in the vertical plane. It was invented in 1992 at Tokyo Institute of Technology by Katsuhisa FurutaXu, Y., Iwase, M. and Furuta, K. (2001) “Time optimal swing-up control of single pendulum”, Journal of Dynamic Systems, Measurement, and Control, 123(3), 518-527.Furuta, K., Iwase, M. (2004) “Swing-up time analysis of pendulum”, Bulletin of the Polish Academy of Sciences: Technical Sciences, 52(3), 153-163.Iwase, M., Åström, K.J., Furuta, K. and Åkesson, J. (2006) “Analysis of safe manual control by using Furuta pendulum”, Proceedings of the IEEE International Conference on Control Applications, 568-572. and his colleagues. It is an example of a complex nonlinear oscillator of interest in control system theory. The pendulum is underactuated and extremely non-linear due to the gravitational fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian Mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the Turin Academy of Science in 1760 culminating in his 1788 grand opus, ''Mécanique analytique''. Lagrangian mechanics describes a mechanical system as a pair consisting of a configuration space (physics), configuration space ''M'' and a smooth function L within that space called a ''Lagrangian''. For many systems, , where ''T'' and ''V'' are the Kinetic energy, kinetic and Potential energy, potential energy of the system, respectively. The stationary action principle requires that the Action (physics)#Action (functional), action functional of the system derived from ''L'' must remain at a stationary point (specifically, a Maximum and minimum, maximum, Maximum and minimum, minimum, or Saddle point, saddle point) throughout the time evoluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pendulum
A pendulum is a device made of a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing. Pendulums were widely used in early mechanical clocks for timekeeping. The regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s. The pendulum clock invented by Christiaan Huygens in 1656 became the world's standard timekeeper, used in homes and offices for 270 years, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centripetal Force
Centripetal force (from Latin ''centrum'', "center" and ''petere'', "to seek") is the force that makes a body follow a curved trajectory, path. The direction of the centripetal force is always orthogonality, orthogonal to the motion of the body and towards the fixed point of the instantaneous osculating circle, center of curvature of the path. Isaac Newton coined the term, describing it as "a force by which bodies are drawn or impelled, or in any way tend, towards a point as to a centre". In Newtonian mechanics, gravity provides the centripetal force causing astronomical orbits. One common example involving centripetal force is the case in which a body moves with uniform speed along a circular path. The centripetal force is directed at right angles to the motion and also along the radius towards the centre of the circular path. The mathematical description was derived in 1659 by the Dutch physicist Christiaan Huygens. Formula From the kinematics of curved motion it is known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coriolis Effect
In physics, the Coriolis force is a pseudo force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term ''Coriolis force'' began to be used in connection with meteorology. Newton's laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. When Newton's laws are transformed to a rotating frame of reference, the Coriolis and centrifugal accelerations appear. When applied ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |