|
Fundamental Modeling Concepts
Fundamental modeling concepts (FMC) provide a framework to describe software-intensive systems. It strongly emphasizes the communication about software-intensive systems by using a semi-formal graphical notation that can easily be understood. Introduction FMC distinguishes three perspectives to look at a software system: * Structure of the system * Processes in the system * Value domains of the system FMC defines a dedicated diagram type for each perspective. FMC diagrams use a simple and lean notation. The purpose of FMC diagrams is to facilitate the communication about a software system, not only between technical experts but also between technical experts and business or domain experts. The comprehensibility of FMC diagrams has made them famous among its supporters. The common approach when working with FMC is to start with a high-level diagram of the compositional structure of a system. This “big picture” diagram serves as a reference in the communication with all invol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Semantics Of Programming Languages
In programming language theory, semantics is the rigorous mathematical study of the meaning of programming languages. Semantics assigns computational meaning to valid string (computer science), strings in a programming language syntax. It is closely related to, and often crosses over with, the Semantics of logic, semantics of mathematical proofs. Semantics describes the processes a computer follows when Execution (computing), executing a program in that specific language. This can be done by describing the relationship between the input and output of a program, or giving an explanation of how the program will be executed on a certain computer platform, platform, thereby creating a model of computation. History In 1967, Robert W. Floyd published the paper ''Assigning meanings to programs''; his chief aim was "a rigorous standard for proofs about computer programs, including formal verification, proofs of correctness, equivalence, and termination". Floyd further wrote: A semant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematics, mathematical field of graph theory, a bipartite graph (or bigraph) is a Graph (discrete mathematics), graph whose vertex (graph theory), vertices can be divided into two disjoint sets, disjoint and Independent set (graph theory), independent sets U and V, that is, every edge (graph theory), edge connects a Vertex (graph theory), vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycle (graph theory), cycles. The two sets U and V may be thought of as a graph coloring, coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a Gallery of named graphs, triangle: after one node is colored blue and another red, the third vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjoint Sets
In set theory in mathematics and Logic#Formal logic, formal logic, two Set (mathematics), sets are said to be disjoint sets if they have no element (mathematics), element in common. Equivalently, two disjoint sets are sets whose intersection (set theory), intersection is the empty set.. For example, and are ''disjoint sets,'' while and are not disjoint. A collection of two or more sets is called disjoint if any two distinct sets of the collection are disjoint. Generalizations This definition of disjoint sets can be extended to family of sets, families of sets and to indexed family, indexed families of sets. By definition, a collection of sets is called a ''family of sets'' (such as the power set, for example). In some sources this is a set of sets, while other sources allow it to be a multiset of sets, with some sets repeated. An \left(A_i\right)_, is by definition a set-valued Function (mathematics), function (that is, it is a function that assigns a set A_i to every ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (graph Theory)
In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another. From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects. The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex ''w'' is said to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
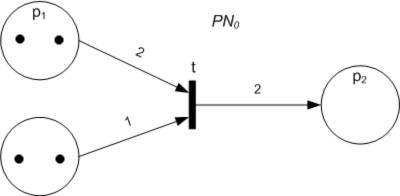
Petri Net
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Modeling
Data modeling in software engineering is the process of creating a data model for an information system by applying certain formal techniques. It may be applied as part of broader Model-driven engineering (MDE) concept. Overview Data modeling is a process used to define and analyze data requirements needed to support the business processes within the scope of corresponding information systems in organizations. Therefore, the process of data modeling involves professional data modelers working closely with business stakeholders, as well as potential users of the information system. There are three different types of data models produced while progressing from requirements to the actual database to be used for the information system.Simison, Graeme. C. & Witt, Graham. C. (2005). ''Data Modeling Essentials''. 3rd Edition. Morgan Kaufmann Publishers. The data requirements are initially recorded as a conceptual data model which is essentially a set of technology independent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Modeling Languages
Data ( , ) are a collection of discrete or continuous values that convey information, describing the quantity, quality, fact, statistics, other basic units of meaning, or simply sequences of symbols that may be further interpreted formally. A datum is an individual value in a collection of data. Data are usually organized into structures such as tables that provide additional context and meaning, and may themselves be used as data in larger structures. Data may be used as variables in a computational process. Data may represent abstract ideas or concrete measurements. Data are commonly used in scientific research, economics, and virtually every other form of human organizational activity. Examples of data sets include price indices (such as the consumer price index), unemployment rates, literacy rates, and census data. In this context, data represent the raw facts and figures from which useful information can be extracted. Data are collected using techniques such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specification Languages
A specification often refers to a set of documented requirements to be satisfied by a material, design, product, or service. A specification is often a type of technical standard. There are different types of technical or engineering specifications (specs), and the term is used differently in different technical contexts. They often refer to particular documents, and/or particular information within them. The word ''specification'' is broadly defined as "to state explicitly or in detail" or "to be specific". A requirement specification is a documented requirement, or set of documented requirements, to be satisfied by a given material, design, product, service, etc. It is a common early part of engineering design and product development processes in many fields. A functional specification is a kind of requirement specification, and may show functional block diagrams. A design or product specification describes the features of the ''solutions'' for the Requirement Specification, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |