|
Fractional-order System
In the fields of dynamical systems and control theory, a fractional-order system is a dynamical system that can be modeled by a fractional differential equation containing derivatives of non-integer order. Such systems are said to have ''fractional dynamics''. Derivatives and integrals of fractional orders are used to describe objects that can be characterized by power-law nonlocality, power-law long-range dependence or fractal properties. Fractional-order systems are useful in studying the anomalous behavior of dynamical systems in physics, electrochemistry, biology, viscoelasticity and chaotic systems. Definition A general dynamical system of fractional order can be written in the form : H(D^)(y_1,y_2,\ldots,y_l) = G(D^)(u_1,u_2,\ldots,u_k) where H and G are functions of the fractional derivative operator D of orders \alpha_1,\alpha_2,\ldots,\alpha_m and \beta_1,\beta_2,\ldots,\beta_n and y_i and u_j are functions of time. A common special case of this is the linear time- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Anomalous Diffusion
Anomalous diffusion is a diffusion process with a non-linear relationship between the mean squared displacement (MSD), \langle r^(\tau )\rangle , and time. This behavior is in stark contrast to Brownian motion, the typical diffusion process described by Albert Einstein and Marian Smoluchowski, where the MSD is linear in time (namely, \langle r^(\tau )\rangle =2dD\tau with ''d'' being the number of dimensions and ''D'' the diffusion coefficient). It has been found that equations describing normal diffusion are not capable of characterizing some complex diffusion processes, for instance, diffusion process in inhomogeneous or heterogeneous medium, e.g. porous media. Fractional diffusion equations were introduced in order to characterize anomalous diffusion phenomena. Examples of anomalous diffusion in nature have been observed in ultra-cold atoms, harmonic spring-mass systems, scalar mixing in the interstellar medium, telomeres in the nucleus of cells, ion channels in the plasm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
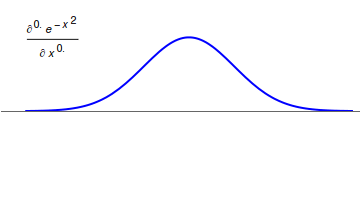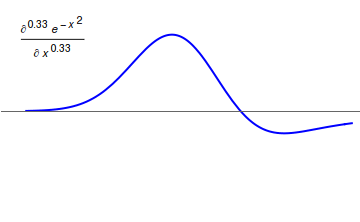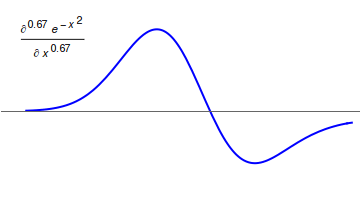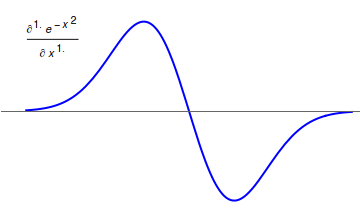 |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar glyphs, such as identities. J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function that is, repeatedly composing D with itself, as in \begin D^n(f) &= (\underbrace_n)(f) \\ &= \underbrace_n (f)\cdots))). \end For example, one may ask for a meaningful interpretation of \sqrt = D^ as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied to any f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Acoustic Attenuation
In acoustics, acoustic attenuation is a measure of the energy loss of sound propagation through an acoustic transmission medium. Most media have viscosity and are therefore not ideal media. When sound propagates in such media, there is always thermal consumption of energy caused by viscosity. This effect can be quantified through the Stokes's law of sound attenuation. Sound attenuation may also be a result of heat conductivity in the media as has been shown by G. Kirchhoff in 1868. The Stokes-Kirchhoff attenuation formula takes into account both viscosity and thermal conductivity effects. For heterogeneous media, besides media viscosity, acoustic scattering is another main reason for removal of acoustic energy. Acoustic attenuation in a lossy medium plays an important role in many scientific researches and engineering fields, such as medical ultrasonography, vibration and noise reduction. Power-law frequency-dependent acoustic attenuation Many experimental and field measureme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Numerical Integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature; others take "quadrature" to include higher-dimensional integration. The basic problem in numerical integration is to compute an approximate solution to a definite integral :\int_a^b f(x) \, dx to a given degree of accuracy. If is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision. Numerical integration has roots in the geometrical problem of finding a square with the same area as a given plane figure ('' quadrature'' or ''squaring''), as in the quadrature of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Linear Multistep Method
Linear multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point. The process continues with subsequent steps to map out the solution. Single-step methods (such as Euler's method) refer to only one previous point and its derivative to determine the current value. Methods such as Runge–Kutta take some intermediate steps (for example, a half-step) to obtain a higher order method, but then discard all previous information before taking a second step. Multistep methods attempt to gain efficiency by keeping and using the information from previous steps rather than discarding it. Consequently, multistep methods refer to several previous points and derivative values. In the case of ''linear'' multistep methods, a linear combination of the previous points and derivative values is used. Definitions Numerical methods ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Fixed Point (mathematics)
In mathematics, a fixed point (sometimes shortened to fixpoint), also known as an invariant point, is a value that does not change under a given transformation (mathematics), transformation. Specifically, for function (mathematics), functions, a fixed point is an element that is mapped to itself by the function. Any set of fixed points of a transformation is also an invariant set. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain of a function, domain and the codomain of , and . In particular, cannot have any fixed point if its domain is disjoint from its codomain. If is defined on the real numbers, it corresponds, in graphical terms, to a curve in the Euclidean plane, and each fixed-point corresponds to an intersection of the curve with the line , cf. picture. For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Fixed-point Theorem
In mathematics, a fixed-point theorem is a result saying that a function ''F'' will have at least one fixed point (a point ''x'' for which ''F''(''x'') = ''x''), under some conditions on ''F'' that can be stated in general terms. In mathematical analysis The Banach fixed-point theorem (1922) gives a general criterion guaranteeing that, if it is satisfied, the procedure of iterating a function yields a fixed point. By contrast, the Brouwer fixed-point theorem (1911) is a non- constructive result: it says that any continuous function from the closed unit ball in ''n''-dimensional Euclidean space to itself must have a fixed point, but it doesn't describe how to find the fixed point (see also Sperner's lemma). For example, the cosine function is continuous in ��1, 1and maps it into ��1, 1 and thus must have a fixed point. This is clear when examining a sketched graph of the cosine function; the fixed point occurs where the cosine curve ''y'' = cos(''x'') intersect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Initial Value Problem
In multivariable calculus, an initial value problem (IVP) is an ordinary differential equation together with an initial condition which specifies the value of the unknown function at a given point in the domain. Modeling a system in physics or other sciences frequently amounts to solving an initial value problem. In that context, the differential initial value is an equation which specifies how the system evolves with time given the initial conditions of the problem. Definition An initial value problem is a differential equation :y'(t) = f(t, y(t)) with f\colon \Omega \subset \mathbb \times \mathbb^n \to \mathbb^n where \Omega is an open set of \mathbb \times \mathbb^n, together with a point in the domain of f :(t_0, y_0) \in \Omega, called the initial condition. A solution to an initial value problem is a function y that is a solution to the differential equation and satisfies :y(t_0) = y_0. In higher dimensions, the differential equation is replaced with a family of eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pyramidal Neurons
Pyramidal cells, or pyramidal neurons, are a type of multipolar neuron found in areas of the brain including the cerebral cortex, the hippocampus, and the amygdala. Pyramidal cells are the primary excitation units of the mammalian prefrontal cortex and the corticospinal tract. One of the main structural features of the pyramidal neuron is the conic shaped soma (biology), soma, or cell body, after which the neuron is named. Other key structural features of the pyramidal cell are a single axon, a large apical dendrite, multiple basal dendrites, and the presence of dendritic spines. Pyramidal neurons are also one of two cell types where the pathognomonic, characteristic Medical sign, sign, Negri bodies, are found in post-mortem rabies infection. Pyramidal neurons were first discovered and studied by Santiago Ramón y Cajal. Since then, studies on pyramidal neurons have focused on topics ranging from neuroplasticity to cognition. Structure One of the main structural features of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Neuroscience
Neuroscience is the scientific study of the nervous system (the brain, spinal cord, and peripheral nervous system), its functions, and its disorders. It is a multidisciplinary science that combines physiology, anatomy, molecular biology, developmental biology, cytology, psychology, physics, computer science, chemistry, medicine, statistics, and mathematical modeling to understand the fundamental and emergent properties of neurons, glia and neural circuits. The understanding of the biological basis of learning, memory, behavior, perception, and consciousness has been described by Eric Kandel as the "epic challenge" of the biological sciences. The scope of neuroscience has broadened over time to include different approaches used to study the nervous system at different scales. The techniques used by neuroscientists have expanded enormously, from molecular and cellular studies of individual neurons to imaging of sensory, motor and cognitive tasks in the brain. Hist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |