|
Fourier Number
In the study of heat conduction, the Fourier number, is the ratio of time, t , to a characteristic time scale for heat diffusion, t_d . This dimensionless group is named in honor of J.B.J. Fourier, who formulated the modern understanding of heat conduction. The time scale for diffusion characterizes the time needed for heat to diffuse over a distance, L . For a medium with thermal diffusivity, \alpha , this time scale is t_d = L^2/\alpha , so that the Fourier number is t/t_d = \alpha t/L^2 . The Fourier number is often denoted as \mathrm or \mathrm_L . The Fourier number can also be used in the study of mass diffusion, in which the thermal diffusivity is replaced by the mass diffusivity. The Fourier number is used in analysis of time-dependent transport phenomena, generally in conjunction with the Biot number if convection is present. The Fourier number arises naturally in nondimensionalization of the heat equation. Definition The general definition of the Four ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Conduction
Thermal conduction is the diffusion of thermal energy (heat) within one material or between materials in contact. The higher temperature object has molecules with more kinetic energy; collisions between molecules distributes this kinetic energy until an object has the same kinetic energy throughout. Thermal conductivity, frequently represented by , is a property that relates the rate of heat loss per unit area of a material to its rate of change of temperature. Essentially, it is a value that accounts for any property of the material that could change the way it conducts heat. Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becomin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meters
The metre (or meter in US spelling; symbol: m) is the base unit of length in the International System of Units (SI). Since 2019, the metre has been defined as the length of the path travelled by light in vacuum during a time interval of of a second, where the second is defined by a hyperfine transition frequency of caesium. The metre was originally defined in 1791 by the French National Assembly as one ten-millionth of the distance from the equator to the North Pole along a great circle, so the Earth's polar circumference is approximately . In 1799, the metre was redefined in terms of a prototype metre bar. The bar used was changed in 1889, and in 1960 the metre was redefined in terms of a certain number of wavelengths of a certain emission line of krypton-86. The current definition was adopted in 1983 and modified slightly in 2002 to clarify that the metre is a measure of proper length. From 1983 until 2019, the metre was formally defined as the length of the path trave ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Diffusion
Molecular diffusion is the motion of atoms, molecules, or other particles of a gas or liquid at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid, size and density (or their product, mass) of the particles. This type of diffusion explains the net flux of molecules from a region of higher concentration to one of lower concentration. Once the concentrations are equal the molecules continue to move, but since there is no concentration gradient the process of molecular diffusion has ceased and is instead governed by the process of self-diffusion, originating from the random motion of the molecules. The result of diffusion is a gradual mixing of material such that the distribution of molecules is uniform. Since the molecules are still in motion, but an equilibrium has been established, the result of molecular diffusion is called a "dynamic equilibrium". In a Phase (matter), phase with uniform temperature, absent external n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Equation
In mathematics and physics (more specifically thermodynamics), the heat equation is a parabolic partial differential equation. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. Since then, the heat equation and its variants have been found to be fundamental in many parts of both pure and applied mathematics. Definition Given an open subset of and a subinterval of , one says that a function is a solution of the heat equation if : \frac = \frac + \cdots + \frac, where denotes a general point of the domain. It is typical to refer to as time and as spatial variables, even in abstract contexts where these phrases fail to have their intuitive meaning. The collection of spatial variables is often referred to simply as . For any given value of , the right-hand side of the equation is the Laplace operator, Laplacian of the function . As such, the heat equation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Conduction
Thermal conduction is the diffusion of thermal energy (heat) within one material or between materials in contact. The higher temperature object has molecules with more kinetic energy; collisions between molecules distributes this kinetic energy until an object has the same kinetic energy throughout. Thermal conductivity, frequently represented by , is a property that relates the rate of heat loss per unit area of a material to its rate of change of temperature. Essentially, it is a value that accounts for any property of the material that could change the way it conducts heat. Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becomin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
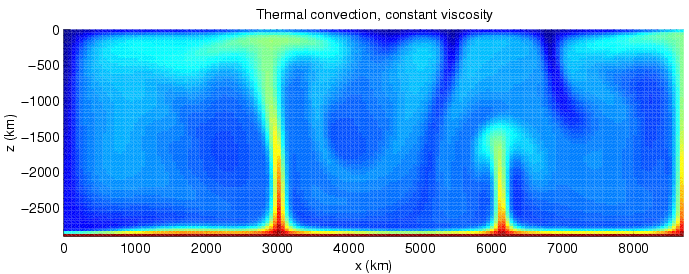
Convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length Scale
In physics, length scale is a particular length or distance determined with the precision of at most a few orders of magnitude. The concept of length scale is particularly important because physical phenomena of different length scales cannot affect each other and are said to decouple. The decoupling of different length scales makes it possible to have a self-consistent theory that only describes the relevant length scales for a given problem. Scientific reductionism says that the physical laws on the shortest length scales can be used to derive the effective description at larger length scales. The idea that one can derive descriptions of physics at different length scales from one another can be quantified with the renormalization group. In quantum mechanics the length scale of a given phenomenon is related to its de Broglie wavelength , where ''ħ'' is the reduced Planck constant and ''p'' is the momentum that is being probed. In relativistic mechanics time and lengt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection (heat Transfer)
Convection (or convective heat transfer) is the heat transfer, transfer of heat from one place to another due to the movement of fluid. Although often discussed as a distinct method of heat transfer, convective heat transfer involves the combined processes of Conduction (heat), conduction (heat diffusion) and advection (heat transfer by bulk fluid flow). Convection is usually the dominant form of heat transfer in liquids and gases. Note that this definition of convection is only applicable in Heat transfer and Thermodynamics, thermodynamic contexts. It should not be confused with the Fluid dynamics, dynamic fluid phenomenon of Convection#Terminology, convection, which is typically referred to as ''Natural Convection'' in thermodynamic contexts in order to distinguish the two. Overview Convection can be "forced" by movement of a fluid by means other than buoyancy forces (for example, a water pump in an automobile engine). Thermal expansion of fluids may also force convection. In o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: \frac = \nabla \cdot \big D(\phi,\mathbf) \ \nabla\phi(\mathbf,t) \big where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second
The second (symbol: s) is a unit of time derived from the division of the day first into 24 hours, then to 60 minutes, and finally to 60 seconds each (24 × 60 × 60 = 86400). The current and formal definition in the International System of Units (SI) is more precise: The second ..is defined by taking the fixed numerical value of the caesium frequency, Δ''ν''Cs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be when expressed in the unit Hz, which is equal to s−1. This current definition was adopted in 1967 when it became feasible to define the second based on fundamental properties of nature with caesium clocks. As the speed of Earth's rotation varies and is slowing ever so slightly, a leap second is added at irregular intervals to civil time to keep clocks in sync with Earth's rotation. The definition that is based on of a rotation of the earth is still used by the Universal Time 1 (UT1) system. Etymology "Minute" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Length
In physics, a characteristic length is an important dimension that defines the scale of a physical system. Often, such a length is used as an input to a formula in order to predict some characteristics of the system, and it is usually required by the construction of a dimensionless quantity, in the general framework of dimensional analysis and in particular applications such as fluid mechanics. In computational mechanics, a characteristic length is defined to force localization of a stress softening constitutive equation. The length is associated with an integration point. For 2D analysis, it is calculated by taking the square root of the area. For 3D analysis, it is calculated by taking the cubic root of the volume associated to the integration point. Examples A characteristic length is usually the volume of a system divided by its surface: L_c = \frac For example, it is used to calculate flow through circular and non-circular tubes in order to examine flow conditions (i.e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |