|
Fokker Periodicity Blocks
Fokker periodicity blocks are a concept in tuning theory used to mathematically relate musical intervals in just intonation to those in equal tuning. They are named after Adriaan Daniël Fokker. These are included as the primary subset of what Erv Wilson refers to as constant structures, where "each interval occurs always subtended by the same number of steps". The basic idea of Fokker's periodicity blocks is to represent just ratios as points on a lattice, and to find vectors in the lattice which represent very small intervals, known as commas. Treating pitches separated by a comma as equivalent "folds" the lattice, effectively reducing its dimension by one; mathematically, this corresponds to finding the quotient group of the original lattice by the sublattice generated by the commas. For an ''n''-dimensional lattice, identifying ''n'' linearly independent commas reduces the dimension of the lattice to zero, meaning that the number of pitches in the lattice is finite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker Periodicity Block 12TET
Fokker (; ) was a Dutch aircraft manufacturer that operated from 1912 to 1996. The company was founded by the Dutch aviator Anthony Fokker and became famous during World War I for its fighter aircraft. During its most successful period in the 1920s and 1930s, Fokker dominated the civil aviation market. The company's fortunes declined over the course of the late 20th century; it declared bankruptcy in 1996, and its operations were sold to competitors. History Fokker in Germany At age 20, while studying in Germany, Anthony Fokker built his initial aircraft, the Fokker Spin, ''Spin'' (Spider)—the first Dutch-built plane to fly in his home country. Taking advantage of better opportunities in Germany, he moved to Berlin, where in 1912, he founded his first company, Fokker Aeroplanbau, later moving to the Görries suburb just southwest of Schwerin (at ), where the current company was founded, as Fokker Aviatik GmbH, on 12 February 1912. World War I Fokker capitalized on having sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
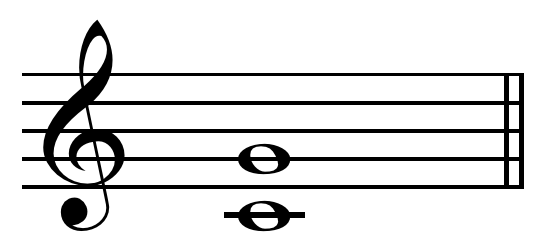
Octave Equivalence
In music, an octave (: eighth) or perfect octave (sometimes called the diapason) is an interval between two notes, one having twice the frequency of vibration of the other. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' (), ''8va bassa'' (, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing this mark above or below the staff. Ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include '' regular tilings'' with regular polygonal tiles all of the same shape, and '' semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An '' aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern (an aperiodic set of prototiles). A '' tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. Three equivalent definitions of ''parallelepiped'' are *a hexahedron with three pairs of parallel faces, *a polyhedron with six faces (hexahedron), each of which is a parallelogram, and *a prism (geometry), prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all special cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; traditionally it was because of its etymology in Ancient Greek, Greek παραλληλεπίπεδον ''parallelepipedon'' (with short -i-), a body "having parallel planes". Parallelepipeds are a subclass of the prismatoids. Properties Any of the three pairs of parallel faces can be viewed as the bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelogram
In Euclidean geometry, a parallelogram is a simple polygon, simple (non-list of self-intersecting polygons, self-intersecting) quadrilateral with two pairs of Parallel (geometry), parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence (geometry), congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations. By comparison, a quadrilateral with at least one pair of parallel sides is a trapezoid in American English or a trapezium in British English. The three-dimensional counterpart of a parallelogram is a parallelepiped. The word "parallelogram" comes from the Greek παραλληλό-γραμμον, ''parallēló-grammon'', which means "a shape of parallel lines". Special cases *Rectangle – A par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Domain
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits. There are many ways to choose a fundamental domain. Typically, a fundamental domain is required to be a connected subset with some restrictions on its boundary, for example, smooth or polyhedral. The images of a chosen fundamental domain under the group action then tile the space. One general construction of fundamental domains uses Voronoi cells. Hints at a general definition Given an action of a group ''G'' on a topological space ''X'' by homeomorphisms, a fundamental domain for this action is a set ''D'' of representatives for the orbits. It is usually required to be a reasonably nice set topologically, in one of several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Lattice
In mathematics, the -dimensional integer lattice (or cubic lattice), denoted , is the lattice (group), lattice in the Euclidean space whose lattice points are tuple, -tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. is the simplest example of a root lattice. The integer lattice is an odd unimodular lattice. Automorphism group The automorphism group (or group (mathematics), group of congruence relation, congruences) of the integer lattice consists of all permutations and sign changes of the coordinates, and is of order of a group, order 2''n'' ''n''!. As a matrix group it is given by the set of all ''n'' × ''n'' signed permutation matrices. This group is group isomorphism, isomorphic to the semidirect product :(\mathbb Z_2)^n \rtimes S_n where the symmetric group ''S''''n'' acts on (Z2)''n'' by permutation (this is a classic example of a wreath product). For the square lattice, this is the group o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Seventh
The harmonic seventh interval, also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio (about 969 cent (music), cents). This is about 32 cents narrower, with a more stable and consonant sound, than a minor seventh in equal temperament, and is up to 49 cents narrower than and is, "particularly sweet", "sweeter in quality" than an "ordinary" minor seventh, just minor seventh, which has an intonation ratio of 9:5 (about 1018 cents). The harmonic seventh arises from the Harmonic series (music), harmonic series as the interval between the fourth harmonic (second octave of the fundamental) and the seventh harmonic; in that octave, harmonics 4, 5, 6, and 7 constitute the four notes (in order) of a purely consonant major chord (root position) with an added minor seventh (or augmented sixth, depending on the tuning system used). Fixed pitch: Not a scale note Although the word "seventh" in the name suggests the seventh note in a scale, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Third
In music theory, a third is a Interval (music), musical interval encompassing three staff positions (see Interval (music)#Number, Interval number for more details), and the major third () is a third spanning four Semitone, half steps or two Whole step, whole steps. Along with the minor third, the major third is one of two commonly occurring thirds. It is described as ''major'' because it is the larger interval of the two: The major third spans four semitones, whereas the minor third only spans three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished third, Diminished and augmented thirds are shown on the musical staff the same number of lines and spaces apart, but contain a different number of semitones in pitch (two and five). Harmonic and non-harmonic thirds The major third may be derived from the harmonic series (music), harmonic series as the interval be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (music)
In music theory, limits or harmonic limits are a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term ''limit'' was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name. The harmonic series and the evolution of music Harry Partch, Ivor Darreg, and Ralph David Hill are among the many microtonalists to suggest that music has been slowly evolving to employ higher and higher harmonics in its constructs (see emancipation of the dissonance). In medieval music, only chords made of octaves and perfect fifths (involving relationships among the first three harmonics) were considered consonant. In the West, triadic harmony arose ( contenance angloise) around the time of the Renaissance, and triads quickly became the fundamental building blocks of Western music. The major and minor thirds of these triads invoke relationships among the fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of the first five consecutive Musical note, notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the Tritone, diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the Harmonic series (music), harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant (music), dominant note is a perfect fifth above the tonic (music), tonic note. The perfect fifth is more consonance and dissonance, consonant, or stable, than any other interval except the unison and the octave. It occu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |