|
Fock Space
The Fock space is an algebraic construction used in quantum mechanics to construct the quantum states space of a variable or unknown number of identical particles from a single particle Hilbert space . It is named after V. A. Fock who first introduced it in his 1932 paper "Konfigurationsraum und zweite Quantelung" (" Configuration space and second quantization"). M.C. Reed, B. Simon, "Methods of Modern Mathematical Physics, Volume II", Academic Press 1975. Page 328. Informally, a Fock space is the sum of a set of Hilbert spaces representing zero particle states, one particle states, two particle states, and so on. If the identical particles are bosons, the -particle states are vectors in a symmetrized tensor product of single-particle Hilbert spaces . If the identical particles are fermions, the -particle states are vectors in an antisymmetrized tensor product of single-particle Hilbert spaces (see symmetric algebra and exterior algebra respectively). A general state in Fock ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication. Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called '' systems of linear equations''. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. Abstract algebra studies algebraic structures, which consist of a set of mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Combination
In mathematics, a linear combination or superposition is an Expression (mathematics), expression constructed from a Set (mathematics), set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' and ''y'' would be any expression of the form ''ax'' + ''by'', where ''a'' and ''b'' are constants). The concept of linear combinations is central to linear algebra and related fields of mathematics. Most of this article deals with linear combinations in the context of a vector space over a field (mathematics), field, with some generalizations given at the end of the article. Definition Let ''V'' be a vector space over the field ''K''. As usual, we call elements of ''V'' ''vector space, vectors'' and call elements of ''K'' ''scalar (mathematics), scalars''. If v1,...,v''n'' are vectors and ''a''1,...,''a''''n'' are scalars, then the ''linear combination of those vectors with those scalars as coefficients'' is :a_1 \mathbf v_1 + a_2 \mathbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inner Product
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in \langle a, b \rangle. Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality (zero inner product) of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or ''scalar product'' of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898. An inner product naturally induces an associated norm, (denoted , x, and , y, in the pictu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm (mathematics)
In mathematics, a norm is a function (mathematics), function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the Origin (mathematics), origin: it Equivariant map, commutes with scaling, obeys a form of the triangle inequality, and zero is only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the #Euclidean norm, Euclidean norm, the #p-norm, 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meaning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tuple
In mathematics, a tuple is a finite sequence or ''ordered list'' of numbers or, more generally, mathematical objects, which are called the ''elements'' of the tuple. An -tuple is a tuple of elements, where is a non-negative integer. There is only one 0-tuple, called the ''empty tuple''. A 1-tuple and a 2-tuple are commonly called a singleton and an ordered pair, respectively. The term ''"infinite tuple"'' is occasionally used for ''"infinite sequences"''. Tuples are usually written by listing the elements within parentheses "" and separated by commas; for example, denotes a 5-tuple. Other types of brackets are sometimes used, although they may have a different meaning. An -tuple can be formally defined as the image of a function that has the set of the first natural numbers as its domain. Tuples may be also defined from ordered pairs by a recurrence starting from an ordered pair; indeed, an -tuple can be identified with the ordered pair of its first elements and its t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fock State
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an important role in the second quantization formulation of quantum mechanics. The particle representation was first treated in detail by Paul Dirac for bosons and by Pascual Jordan and Eugene Wigner for fermions. The Fock states of bosons and fermions obey useful relations with respect to the Fock space creation and annihilation operators. Definition One specifies a multiparticle state of ''N'' non-interacting identical particles by writing the state as a sum of tensor products of ''N'' one-particle states. Additionally, depending on the integrality of the particles' spin, the tensor products must be alternating (anti-symmetric) or symmetric products of the underlying one-particle Hilbert spaces. Specifically: * Fermions, having half- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Tensor
In mathematics and theoretical physics, a tensor is antisymmetric or alternating on (or with respect to) an index subset if it alternates sign (+/−) when any two indices of the subset are interchanged. section §7. The index subset must generally either be all ''covariant'' or all ''contravariant''. For example, T_ = -T_ = T_ = -T_ = T_ = -T_ holds when the tensor is antisymmetric with respect to its first three indices. If a tensor changes sign under exchange of ''each'' pair of its indices, then the tensor is completely (or totally) antisymmetric. A completely antisymmetric covariant tensor field of order k may be referred to as a differential k-form, and a completely antisymmetric contravariant tensor field may be referred to as a k-vector field. Antisymmetric and symmetric tensors A tensor A that is antisymmetric on indices i and j has the property that the contraction with a tensor B that is symmetric on indices i and j is identically 0. For a general tensor U with comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Tensor
In mathematics, a symmetric tensor is an unmixed tensor that is invariant under a permutation of its vector arguments: :T(v_1,v_2,\ldots,v_r) = T(v_,v_,\ldots,v_) for every permutation ''σ'' of the symbols Alternatively, a symmetric tensor of order ''r'' represented in coordinates as a quantity with ''r'' indices satisfies :T_ = T_. The space of symmetric tensors of order ''r'' on a finite-dimensional vector space ''V'' is naturally isomorphic to the dual of the space of homogeneous polynomials of degree ''r'' on ''V''. Over fields of characteristic zero, the graded vector space of all symmetric tensors can be naturally identified with the symmetric algebra on ''V''. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering, physics and mathematics. Definition Let ''V'' be a vector space and :T\in V^ a tensor of order ''k''. Then ''T'' is a symmetric tensor if :\tau_\sigma T = T\, for the braiding ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
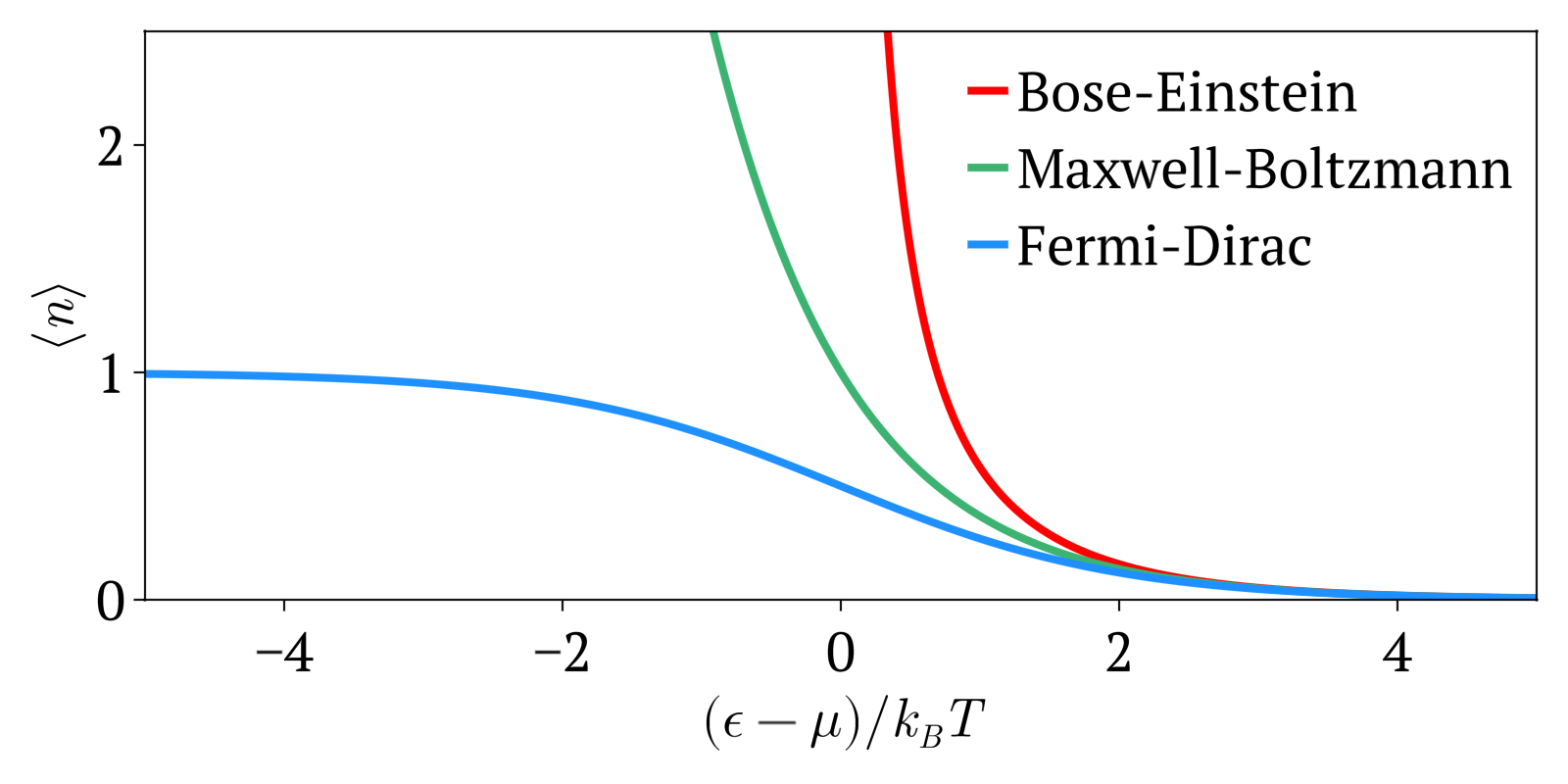
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bose–Einstein Statistics
In quantum statistics, Bose–Einstein statistics (B–E statistics) describes one of two possible ways in which a collection of non-interacting identical particles may occupy a set of available discrete energy states at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles could be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Bose. Bose–Einstein statistics apply only to particles that do not follow the Pauli exclusion principle restrictions. Particles that follow Bose-Einstein statistics are called bosons, which have integer values of spin. In contrast, particles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator (physics)
An operator is a function over a space of physical states onto another space of states. The simplest example of the utility of operators is the study of symmetry (which makes the concept of a group useful in this context). Because of this, they are useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory. They play a central role in describing observables (measurable quantities like energy, momentum, etc.). Operators in classical mechanics In classical mechanics, the movement of a particle (or system of particles) is completely determined by the Lagrangian L(q, \dot, t) or equivalently the Hamiltonian H(q, p, t), a function of the generalized coordinates ''q'', generalized velocities \dot = \mathrm q / \mathrm t and its conjugate momenta: :p = \frac If either ''L'' or ''H'' is independent of a generalized coordinate ''q'', meaning the ''L'' and ''H'' do not change when ''q' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |