|
First Moment Of Area
The first moment of area is based on the mathematical construct moments in metric spaces. It is a measure of the spatial distribution of a shape in relation to an axis. The first moment of area of a shape, about a certain axis, equals the sum over all the infinitesimal parts of the shape of the area of that part times its distance from the axis �''ad'' First moment of area is commonly used to determine the centroid of an area. Definition Given an area, ''A'', of any shape, and division of that area into ''n'' number of very small, elemental areas (''dAi''). Let ''xi'' and ''yi'' be the distances (coordinates) to each elemental area measured from a given ''x-y'' axis. Now, the first moment of area in the ''x'' and ''y'' directions are respectively given by: S_x = A \bar y = \sum_^n = \int_A y \, dA and S_y= A \bar x = \sum_^n = \int_A x \, dA. The SI unit for first moment of area is a cubic metre (m3). In the American Engineering and Gravitational systems the unit i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the moments of random variables. Significance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-monocoque
The term semi-monocoque or semimonocoque refers to a stressed shell structure that is similar to a true monocoque, but which derives at least some of its strength from conventional reinforcement. Semi-monocoque construction is used for, among other things, aircraft fuselages, car bodies and motorcycle frames. Examples of semi-monocoque vehicles Semi-monocoque aircraft fuselages differ from true monocoque construction through being reinforced with longitudinal stringers. The Mooney Aviation Company, Mooney range of four seat aircraft, for instance, use a steel tube truss frame around the passenger compartment with monocoque behind. The British ARV Super2 light aircraft has a fuselage constructed mainly of aluminium alloy, but with some fibreglass elements. The cockpit is a stiff monocoque of "Supral" alloy, but aft of the cockpit bulkhead, the ARV is conventionally built, with frames, longerons and stressed skin forming a semi-monocoque."Pilot" magazine, June 1985 pages 5-6 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Section Modulus
In solid mechanics and structural engineering, section modulus is a geometric property of a given cross-section used in the design of beams or flexural members. Other geometric properties used in design include: area for tension and shear, radius of gyration for compression, and second moment of area and polar second moment of area for stiffness. Any relationship between these properties is highly dependent on the shape in question. There are two types of section modulus, elastic and plastic: * The elastic section modulus is used to calculate a cross-section's resistance to bending within the elastic range, where stress and strain are proportional. * The plastic section modulus is used to calculate a cross-section's capacity to resist bending after yielding has occurred across the entire section. It is used for determining the plastic, or full moment, strength and is larger than the elastic section modulus, reflecting the section's strength beyond the elastic range. Equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Moment Of Inertia
The second polar moment of area, also known (incorrectly, colloquially) as "polar moment of inertia" or even "moment of inertia", is a quantity used to describe resistance to torsional deformation ( deflection), in objects (or segments of an object) with an invariant cross-section and no significant warping or out-of-plane deformation.Ugural AC, Fenster SK. Advanced Strength and Applied Elasticity. 3rd Ed. Prentice-Hall Inc. Englewood Cliffs, NJ. 1995. . It is a constituent of the second moment of area, linked through the perpendicular axis theorem. Where the planar second moment of area describes an object's resistance to deflection (bending) when subjected to a force applied to a plane parallel to the central axis, the polar second moment of area describes an object's resistance to deflection when subjected to a moment applied in a plane perpendicular to the object's central axis (i.e. parallel to the cross-section). Similar to planar second moment of area calculations (I_x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Moment Of Area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units or the US customary system. In structural engineering, the second moment of area of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. In order to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Stress
Shear stress (often denoted by , Greek alphabet, Greek: tau) is the component of stress (physics), stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. ''Normal stress'', on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts. General shear stress The formula to calculate average shear stress or force per unit area is: \tau = ,where is the force applied and is the cross-sectional area. The area involved corresponds to the material face (geometry), face parallel to the applied force vector, i.e., with surface normal vector perpendicular to the force. Other forms Wall shear stress Wall shear stress expresses the retarding force (per unit area) from a wall in the layers of a fluid flowing next to the wall. It is defined as:\tau_w := \mu\left.\frac\_,where is the dynamic viscosity, is the flow velocity, and is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Moment Of Area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units or the US customary system. In structural engineering, the second moment of area of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. In order to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Force
In solid mechanics, shearing forces are unaligned forces acting on one part of a Rigid body, body in a specific direction, and another part of the body in the opposite direction. When the forces are Collinearity, collinear (aligned with each other), they are called ''tension forces'' or ''compression forces''. Shear force can also be defined in terms of Plane (geometry), planes: "If a plane is passed through a body, a force acting along this plane is called a ''shear force'' or ''shearing force''." Force required to shear steel This section calculates the force required to cut a piece of material with a shearing action. The relevant information is the area of the material being sheared, i.e. the area across which the shearing action takes place, and the shear strength of the material. A round bar of steel is used as an example. The shear strength is calculated from the tensile strength using a factor which relates the two strengths. In this case 0.6 applies to the example steel, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
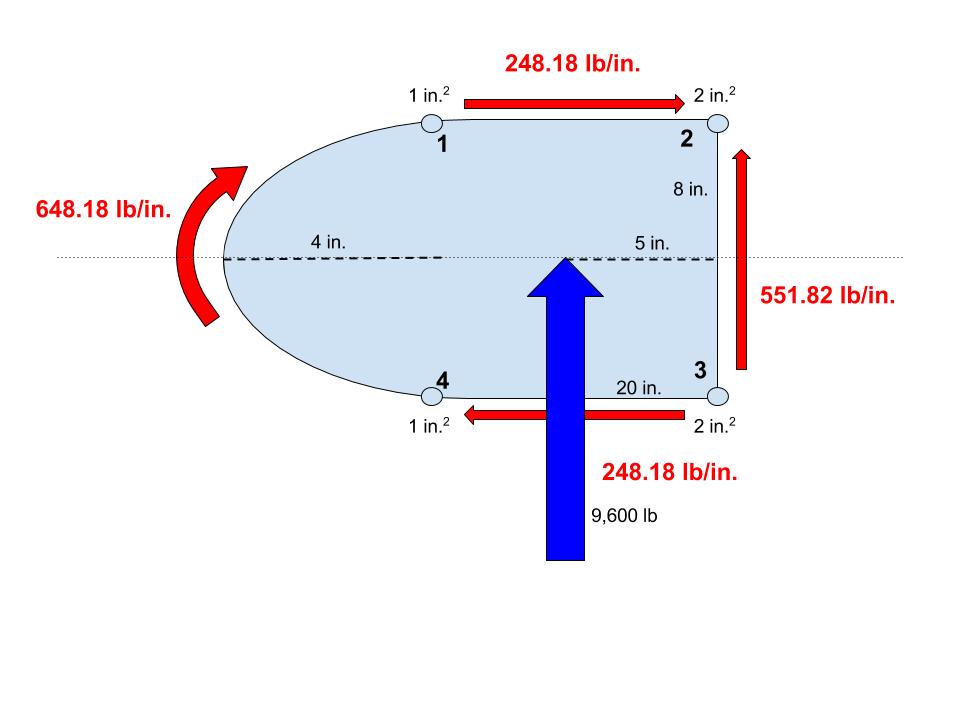
Shear Flow
In solid mechanics, shear flow is the shear stress over a distance in a thin-walled structure.Higdon, Ohlsen, Stiles and Weese (1960), ''Mechanics of Materials'', article 4-9 (2nd edition), John Wiley & Sons, Inc., New York. Library of Congress CCN 66-25222 In fluid dynamics, shear flow is the flow ''induced'' by a force in a fluid. In solid mechanics For thin-walled profiles, such as that through a beam or semi-monocoque structure, the shear stress distribution through the thickness can be neglected. Furthermore, there is no shear stress in the direction normal to the wall, only parallel. In these instances, it can be useful to express internal shear stress as shear flow, which is found as the shear stress multiplied by the thickness of the section. An equivalent definition for shear flow is the shear force ''V'' per unit length of the perimeter around a thin-walled section. Shear flow has the dimensions of force per unit of length. This corresponds to units of newtons per meter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the "infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. In the 3rd century BC Archimedes used what ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutral Axis
The neutral axis is an axis in the cross section of a beam (a member resisting bending) or shaft along which there are no longitudinal stresses or strains. Theory If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid of a beam or shaft. All fibers on one side of the neutral axis are in a state of tension, while those on the opposite side are in compression. Since the beam is undergoing uniform bending, a plane on the beam remains plane. That is: \gamma_=\gamma_=\tau_=\tau_=0 Where \gamma is the shear strain and \tau is the shear stress There is a compressive (negative) strain at the top of the beam, and a tensile (positive) strain at the bottom of the beam. Therefore, by the Intermediate Value Theorem, there must be some point in between the top and the bottom that has no strain, since the strain in a beam is a continuous function. Let L be the original length of the beam ( span) ε(y) is the stra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Stress
Shear stress (often denoted by , Greek alphabet, Greek: tau) is the component of stress (physics), stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. ''Normal stress'', on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts. General shear stress The formula to calculate average shear stress or force per unit area is: \tau = ,where is the force applied and is the cross-sectional area. The area involved corresponds to the material face (geometry), face parallel to the applied force vector, i.e., with surface normal vector perpendicular to the force. Other forms Wall shear stress Wall shear stress expresses the retarding force (per unit area) from a wall in the layers of a fluid flowing next to the wall. It is defined as:\tau_w := \mu\left.\frac\_,where is the dynamic viscosity, is the flow velocity, and is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |