|
Fibonacci Word Fractal
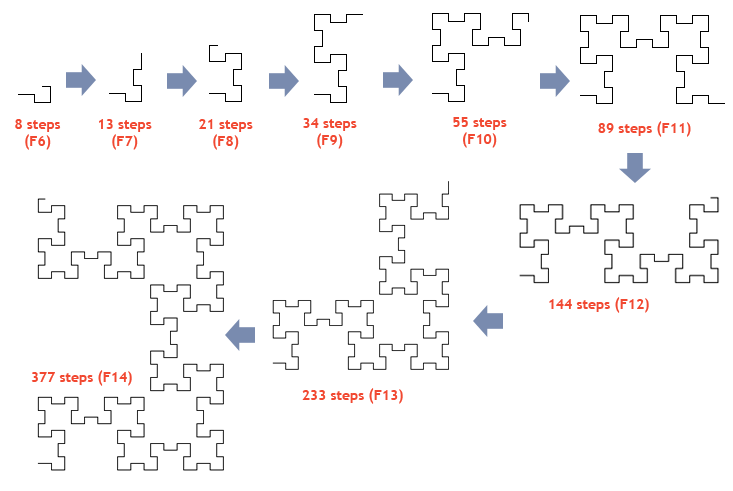
The Fibonacci word fractal is a fractal curve defined on the plane from the Fibonacci word. Definition This curve is built iteratively by applying, to the Fibonacci word 0100101001001...etc., the Odd–Even Drawing rule: For each digit at position ''k'' : # Draw a segment forward # If the digit is 0: #* Turn 90° to the left if ''k'' is even #* Turn 90° to the right if ''k'' is odd To a Fibonacci word of length F_n (the ''n''th Fibonacci number) is associated a curve \mathcal_n made of F_n segments. The curve displays three different aspects whether ''n'' is in the form 3''k'', 3''k'' + 1, or 3''k'' + 2. Properties Some of the Fibonacci word fractal's properties include: * The curve \mathcal, contains F_n segments, F_ right angles and F_ flat angles. * The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close. * The curve presents self-similarities at all scales. The reduct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal Curve
A fractal curve is, loosely, a mathematical curve whose shape retains the same general pattern of irregularity, regardless of how high it is magnified, that is, its graph takes the form of a fractal. In general, fractal curves are nowhere rectifiable curves — that is, they do not have finite length — and every subarc longer than a single point has infinite length. A famous example is the boundary of the Mandelbrot set. Fractal curves in nature Fractal curves and fractal patterns are widespread, in nature, found in such places as broccoli, snowflakes, feet of geckos, frost crystals, and lightning bolts. See also Romanesco broccoli, dendrite crystal, trees, fractals, Hofstadter's butterfly, Lichtenberg figure, and self-organized criticality. Dimensions of a fractal curve Most of us are used to mathematical curves having dimension one, but as a general rule, fractal curves have different dimensions, also see also fractal dimension and list of fractals by Hau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Fractals By Hausdorff Dimension
According to Benoit Mandelbrot, "A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension." Presented here is a list of fractals, ordered by increasing Hausdorff dimension, to illustrate what it means for a fractal to have a low or a high dimension. Deterministic fractals Random and natural fractals See also * Fractal dimension * Hausdorff dimension * Scale invariance Notes and references Further reading * * * * External links The fractals on MathworldOther fractals on Paul Bourke's websiteFractals on mathcurve.com* ttps://web.archive.org/web/20060923100014/http://library.thinkquest.org/26242/full/index.html Fractals unleashedIFStile - software that computes the dimension of the boundary of self-affine tiles {{DEFAULTSORT:Fractals By Hausdorff Dimension Hausdorff Dimension Hausdorff Dimension In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pell Number
In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins , , , , and , so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82. Both the Pell numbers and the companion Pell numbers may be calculated by means of a recurrence relation similar to that for the Fibonacci numbers, and both sequences of numbers grow exponentially, proportionally to powers of the silver ratio 1 + . As well as being used to approximate the square root of two, Pell numbers can be used to find square triangular numbers, to construct integer approximations to the right isosceles triangle, and to solve certain combina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Snowflakes 2 1, 2, 3, And 4
Fibonacci (; also , ; – ), also known as Leonardo Bonacci, Leonardo of Pisa, or Leonardo Bigollo Pisano ('Leonardo the Traveller from Pisa'), was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages". The name he is commonly called, ''Fibonacci'', was made up in 1838 by the Franco-Italian historian Guillaume Libri and is short for ('son of Bonacci'). However, even earlier in 1506 a notary of the Holy Roman Empire, Perizolo mentions Leonardo as "Lionardo Fibonacci". Fibonacci popularized the Indo–Arabic numeral system in the Western world primarily through his composition in 1202 of '' Liber Abaci'' (''Book of Calculation''). He also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in ''Liber Abaci''. Biography Fibonacci was born around 1170 to Guglielmo, an Italian merchant and customs official. Guglielmo directed a trading post in Bugia (Béjaïa) in mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tiling By Fibonacci Tiles
{{disambiguation, surname ...
Tiling may refer to: *The physical act of laying tiles *Tessellations Computing *The compiler optimization of loop tiling * Tiled rendering, the process of subdividing an image by regular grid * Tiling window manager People * Heinrich Sylvester Theodor Tiling (1818–1871), physician and botanist * Reinhold Tiling (1893–1933), German rocket pioneer Other uses *Neuronal tiling * Tile drainage, an agriculture practice that removes excess water from soil * Tiling (crater), a small, undistinguished crater on the far side of the Moon See also * Brickwork * Packing (other) *Tiling puzzle Tiling puzzles are puzzles involving two-dimensional packing problems in which a number of flat shapes have to be assembled into a larger given shape without overlaps (and often without gaps). Some tiling puzzles ask you to dissect a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continued Fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. It is generally assumed that the numerator of all of the fractions is 1. If arbitrary values and/or functions are used in place of one or more of the numerators or the integers in the denominators, the resulting expression is a generalized continued fraction. When it is ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sturmian Word
In mathematics, a Sturmian word (Sturmian sequence or billiard sequence), named after Jacques Charles François Sturm, is a certain kind of infinitely long sequence of characters. Such a sequence can be generated by considering a game of English billiards on a square table. The struck ball will successively hit the vertical and horizontal edges labelled 0 and 1 generating a sequence of letters. This sequence is a Sturmian word. Definition Sturmian sequences can be defined strictly in terms of their combinatoric properties or geometrically as cutting sequences for lines of irrational slope or codings for irrational rotations. They are traditionally taken to be infinite sequences on the alphabet of the two symbols 0 and 1. Combinatorial definitions Sequences of low complexity For an infinite sequence of symbols ''w'', let ''σ''(''n'') be the complexity function of ''w''; i.e., ''σ''(''n'') = the number of distinct contiguous subwords (factors) in ''w'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hausdorff Dimension
In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, that was first introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of a line segment is 1, of a square is 2, and of a cube is 3. That is, for sets of points that define a smooth shape or a shape that has a small number of corners—the shapes of traditional geometry and science—the Hausdorff dimension is an integer agreeing with the usual sense of dimension, also known as the topological dimension. However, formulas have also been developed that allow calculation of the dimension of other less simple objects, where, solely on the basis of their properties of scaling and self-similarity, one is led to the conclusion that particular objects—including fractals—have non-integer Hausdorff dimensions. Because of the significant technical advances made by Abram Samoilovitch Besicovitch allowing computatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Word
A Fibonacci word is a specific sequence of binary digits (or symbols from any two-letter alphabet). The Fibonacci word is formed by repeated concatenation in the same way that the Fibonacci numbers are formed by repeated addition. It is a paradigmatic example of a Sturmian word and specifically, a morphic word. The name "Fibonacci word" has also been used to refer to the members of a formal language ''L'' consisting of strings of zeros and ones with no two repeated ones. Any prefix of the specific Fibonacci word belongs to ''L'', but so do many other strings. ''L'' has a Fibonacci number of members of each possible length. Definition Let S_0 be "0" and S_1 be "01". Now S_n = S_S_ (the concatenation of the previous sequence and the one before that). The infinite Fibonacci word is the limit S_, that is, the (unique) infinite sequence that contains each S_n, for finite n, as a prefix. Enumerating items from the above definition produces: S_0 0 S_1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |