|
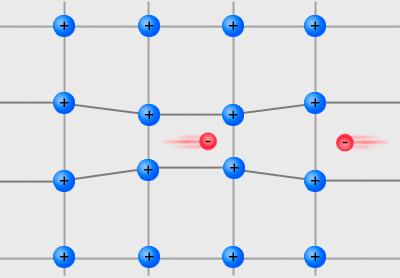
Fermi Gas
A Fermi gas is an idealized model, an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi. This physical model is useful for certain systems with many fermions. Some key examples are the behaviour of charge carriers in a metal, nucleons in an atomic nucleus, neutrons in a neutron star, and electrons in a white dwarf. Description An ideal Fermi gas or free Fermi gas is a physical model assuming a collection of non-interacting fermions in a constant potential well. Fermions are elementary or composite particles with half-integer spin, thus follow Fermi–Dirac statistics. The e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degeneracy Pressure
In astrophysics and condensed matter physics, electron degeneracy pressure is a quantum mechanical effect critical to understanding the stability of white dwarf stars and metal solids. It is a manifestation of the more general phenomenon of quantum degeneracy pressure. The term "degenerate" here is not related to degenerate energy levels, but to Fermi–Dirac statistics close to the zero-temperature limit (temperatures much smaller than the Fermi temperature, which for metals is about 10,000 K.) In metals and in white dwarf stars, electrons can be modeled as a gas of non-interacting electrons confined to a finite volume. Although there are strong electromagnetic forces between the negatively charged electrons, these forces are approximately balanced by the positive nuclei and so can be neglected in the simplest models. The pressure exerted by the electrons is related to their kinetic energy. The degeneracy pressure is most prominent at low temperatures: If electrons wer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various #Units, units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the International System of Units, SI unit of pressure, the Pascal (unit), pascal (Pa), for example, is one newton (unit), newton per square metre (N/m2); similarly, the Pound (force), pound-force per square inch (Pound per square inch, psi, symbol lbf/in2) is the traditional unit of pressure in the imperial units, imperial and United States customary units, US customary systems. Pressure ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ground State
The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. In quantum field theory, the ground state is usually called the vacuum. If more than one ground state exists, they are said to be degenerate. Many systems have degenerate ground states. Degeneracy occurs whenever there exists a unitary operator that acts non-trivially on a ground state and commutes with the Hamiltonian of the system. According to the third law of thermodynamics, a system at absolute zero temperature exists in its ground state; thus, its entropy is determined by the degeneracy of the ground state. Many systems, such as a perfect crystal lattice, have a unique ground state and therefore have zero entropy at absolute zero. It is also possible for the highest excited state to have absolute zero temperature for sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Zero
Absolute zero is the lowest possible temperature, a state at which a system's internal energy, and in ideal cases entropy, reach their minimum values. The absolute zero is defined as 0 K on the Kelvin scale, equivalent to −273.15 °C on the Celsius, Celsius scale, and −459.67 °F on the Fahrenheit scale. The Kelvin and Rankine temperature scales set their zero points at absolute zero by design. This limit can be estimated by extrapolating the ideal gas law to the temperature at which the volume or pressure of a classical gas becomes zero. At absolute zero, there is no thermal motion. However, due to quantum mechanics, quantum effects, the particles still exhibit minimal motion mandated by the Uncertainty principle, Heisenberg uncertainty principle and, for a system of fermions, the Pauli exclusion principle. Even if absolute zero could be achieved, this residual quantum motion would persist. Although absolute zero can be approached, it cannot be reached. Som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
BCS Theory
In physics, the Bardeen–Cooper–Schrieffer (BCS) theory (named after John Bardeen, Leon Cooper, and John Robert Schrieffer) is the first microscopic theory of superconductivity since Heike Kamerlingh Onnes's 1911 discovery. The theory describes superconductivity as a microscopic effect caused by a condensation of Cooper pairs. The theory is also used in nuclear physics to describe the pairing interaction between nucleons in an atomic nucleus. It was proposed by Bardeen, Cooper, and Schrieffer in 1957; they received the Nobel Prize in Physics for this theory in 1972. History Rapid progress in the understanding of superconductivity gained momentum in the mid-1950s. It began with the 1948 paper, "On the Problem of the Molecular Theory of Superconductivity", where Fritz London proposed that the phenomenological London equations may be consequences of the coherence of a quantum state. In 1953, Brian Pippard, motivated by penetration experiments, proposed that this would mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cooper Pair
In condensed matter physics, a Cooper pair or BCS pair (Bardeen–Cooper–Schrieffer pair) is a pair of electrons (or other fermions) bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper. Description Cooper showed that an arbitrarily small attraction between electrons in a metal can cause a paired state of electrons to have a lower energy than the Fermi energy, which implies that the pair is bound. In conventional superconductors, this attraction is due to the electron–phonon interaction. The Cooper pair state is responsible for superconductivity, as described in the BCS theory developed by John Bardeen, Leon Cooper, and John Schrieffer for which they shared the 1972 Nobel Prize in Physics. Although Cooper pairing is a quantum effect, the reason for the pairing can be seen from a simplified classical explanation. An electron in a metal normally behaves as a free particle. The electron is repelled from other electrons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
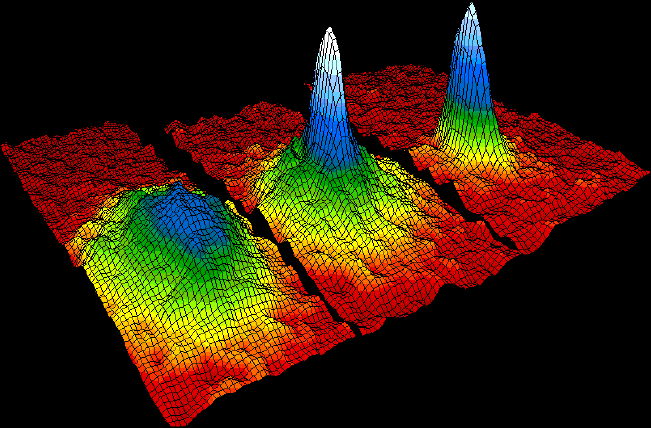
Bose–Einstein Condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low Density, densities is cooled to temperatures very close to absolute zero#Relation with Bose–Einstein condensate, absolute zero, i.e. . Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which microscopic Quantum mechanics, quantum-mechanical phenomena, particularly wave interference#Quantum interference, wavefunction interference, become apparent Macroscopic quantum phenomena, macroscopically. More generally, condensation refers to the appearance of macroscopic occupation of one or several states: for example, in BCS theory, a superconductor is a condensate of Cooper pairs. As such, condensation can be associated with phase transition, and the macroscopic occupation of the state is the order parameter. Bose–Einstein condensate was first predicted, generally, in 1924–1925 by Albert Einstein, credit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Number
In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence. Quantum numbers are closely related to eigenvalues of observables. When the corresponding observable commutes with the Hamiltonian of the system, the quantum number is said to be " good", and acts as a constant of motion in the quantum dynamics. History Electronic quantum numbers In the era of the old quantum theory, starting from Max Planck's proposal of quanta in his model of blackbody radiation (1900) and Albert Einstein's adaptation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum State
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Exclusion Principle
In quantum mechanics, the Pauli exclusion principle (German: Pauli-Ausschlussprinzip) states that two or more identical particles with half-integer spins (i.e. fermions) cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940. In the case of electrons in atoms, the exclusion principle can be stated as follows: in a poly-electron atom it is impossible for any two electrons to have the same two values of ''all'' four of their quantum numbers, which are: ''n'', the principal quantum number; ', the azimuthal quantum number; ''m'', the magnetic quantum number; and ''ms'', the spin quantum number. For example, if two electrons reside in the same orbital, then their values of ''n'', ', and ''m'' are equal. In that case, the two values of ''m''s (spin) pair must be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions. Under various conditions of temperature and pressure, many real gases behave qualitatively like an ideal gas where the gas molecules (or atoms for monatomic gas) play the role of the ideal particles. Many gases such as nitrogen, oxygen, hydrogen, noble gases, some heavier gases like carbon dioxide and mixtures such as air, can be treated as ideal gases within reasonable tolerances over a considerable parameter range around standard temperature and pressure. Generally, a gas behaves more like an ideal gas at higher temperature and lower ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |