|
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as: \operatorname z = \frac\int_0^z e^\,\mathrm dt. The integral here is a complex Contour integration, contour integral which is path-independent because \exp(-t^2) is Holomorphic function, holomorphic on the whole complex plane \mathbb. In many applications, the function argument is a real number, in which case the function value is also real. In some old texts, the error function is defined without the factor of \frac. This nonelementary integral is a sigmoid function, sigmoid function that occurs often in probability, statistics, and partial differential equations. In statistics, for non-negative real values of , the error function has the following interpretation: for a real random variable that is normal distribution, normally distributed with mean 0 and standard deviation \frac, is the probability that falls in the range . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contour Integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane. Contour integration is closely related to the Residue theorem, calculus of residues, a method of complex analysis. One use for contour integrals is the evaluation of integrals along the real line that are not readily found by using only real variable methods. It also has various applications in physics. Contour integration methods include: * direct integration of a complex number, complex-valued function along a curve in the complex plane * application of the Cauchy integral formula * application of the residue theorem One method can be used, or a combination of these methods, or various limiting processes, for the purpose of finding these integrals or sums. Curves in the complex plane In complex analysis, a contour is a type of curve in the complex plane. In contour integration, contours provide a precise definition of the curves on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Expansion
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Integral
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function f(x) = e^ over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is \int_^\infty e^\,dx = \sqrt. Abraham de Moivre originally discovered this type of integral in 1733, while Gauss published the precise integral in 1809, attributing its discovery to Laplace. The integral has a wide range of applications. For example, with a slight change of variables it is used to compute the normalizing constant of the normal distribution. The same integral with finite limits is closely related to both the error function and the cumulative distribution function of the normal distribution. In physics this type of integral appears frequently, for example, in quantum mechanics, to find the probability density of the ground state of the harmonic oscillator. This integral is also used in the path integral formulation, to find the propagator of the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
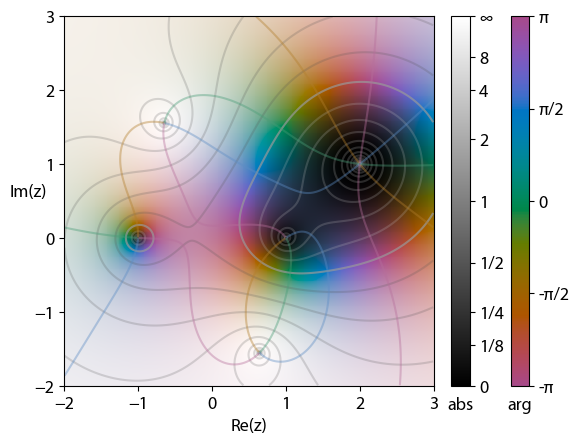
Domain Coloring
In complex analysis, domain coloring or a color wheel graph is a technique for visualizing complex functions by assigning a color to each point of the complex plane. By assigning points on the complex plane to different colors and brightness, domain coloring allows for a function from the complex plane to itself, whose graph would normally require four spatial dimensions, to be easily represented and understood. This provides insight to the fluidity of complex functions and shows natural geometric extensions of real functions. Motivation A graph of a real function can be drawn in two dimensions because there are two represented variables, x and y. However, complex numbers are represented by two variables and therefore two dimensions; this means that representing a complex function (more precisely, a complex-valued function of one complex variable f: \mathbb \to \mathbb) requires the visualization of four dimensions. One way to achieve that is with a Riemann surface, but anothe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, if r and \varphi are real numbers then the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entire Function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z-w), taking the limit value at w, is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function. A transcendental entire function is an entire function that is not a polynomial. Just as meromorphic functions can be viewed as a generalization of rational fractions, entire functions can be viewed as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Even Function
In mathematics, an even function is a real function such that f(-x)=f(x) for every x in its domain. Similarly, an odd function is a function such that f(-x)=-f(x) for every x in its domain. They are named for the parity of the powers of the power functions which satisfy each condition: the function f(x) = x^n is even if ''n'' is an even integer, and it is odd if ''n'' is an odd integer. Even functions are those real functions whose graph is self-symmetric with respect to the and odd functions are those whose graph is self-symmetric with respect to the origin. If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely decomposed as the sum of an even function and an odd function. Early history The concept of even and odd functions appears to date back to the early 18th century, with Leonard Euler playing a significant role in their formalization. Euler introduced the concepts of even and odd functions (using La ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
With High Probability
In mathematics, an event that occurs with high probability (often shortened to w.h.p. or WHP) is one whose probability depends on a certain number ''n'' and goes to 1 as ''n'' goes to infinity, i.e. the probability of the event occurring can be made as close to 1 as desired by making ''n'' big enough. Applications The term WHP is especially used in computer science, in the analysis of probabilistic algorithms. For example, consider a certain probabilistic algorithm on a graph with ''n'' nodes. If the probability that the algorithm returns the correct answer is 1-1/n, then when the number of nodes is very large, the algorithm is correct with a probability that is very near 1. This fact is expressed shortly by saying that the algorithm is correct WHP. Some examples where this term is used are: * Miller–Rabin primality test: a probabilistic algorithm for testing whether a given number ''n'' is prime or composite. If ''n'' is composite, the test will detect ''n'' as composite WHP. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heaviside Step Function
The Heaviside step function, or the unit step function, usually denoted by or (but sometimes , or ), is a step function named after Oliver Heaviside, the value of which is zero for negative arguments and one for positive arguments. Different conventions concerning the value are in use. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely. Heaviside developed the operational calculus as a tool in the analysis of telegraphic communications and represented the function as . Formulation Taking the convention that , the Heaviside function may be defined as: * a piecewise function: H(x) := \begin 1, & x \geq 0 \\ 0, & x * an indicator function: H(x) := \mathbf_=\mathbf 1_(x) For the al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |