|
Equal-area Projection
In cartography, an equivalent, authalic, or equal-area projection is a map projection that preserves relative area measure between any and all map regions. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, and so forth, because an equal-area map does not change apparent density of the phenomenon being mapped. By Carl Friedrich Gauss, Gauss's Theorema Egregium, an equal-area projection cannot be conformal map projection, conformal. This implies that an equal-area projection inevitably distorts shapes. Even though a point or points or a path or paths on a map might have no distortion, the greater the area of the region being mapped, the greater and more obvious the distortion of shapes inevitably becomes. Description In order for a map projection of the sphere to be equal-area, its generating formulae must meet this Cauchy-Riemann equations, Cauchy-Riemann-like condition: :\frac \cdo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Equal-area Projection
In cartography, the normal cylindrical equal-area projection is a family of Map projection#Normal cylindrical, normal cylindrical, equal-area projection, equal-area map projections. History The invention of the Lambert cylindrical equal-area projection is attributed to the Switzerland, Swiss mathematician Johann Heinrich Lambert in 1772. Variations of it appeared over the years by inventors who stretched the height of the Lambert and compressed the width commensurately in various ratios. Description The projection: * is Map_projection#Cylindrical, cylindrical, that means it has a cylindrical projection surface * is normal, that means it has a normal Map projection#Aspect, aspect * is an equal-area projection, that means any two areas in the map have the same relative size compared to their size on the sphere. The term "normal cylindrical projection" is used to refer to any projection in which Meridian (geography), meridians are mapped to equally spaced vertical lines and cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mollweide Projection SW
Mollweide may refer to: *Karl Mollweide, mathematician (1774–1825). :*Mollweide projection, a pseudocylindrical map projection. :*Mollweide Glacier, a glacier the Victoria region of Antarctica. :*Mollweide's formula, a mathematical equation. {{dab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Azimuthal Equal-area Projection
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection. The Lambert azimuthal projection is used as a map projection in cartography. For example, the National Atlas of the US uses a Lambert azimuthal equal-area projection to display information in the online Map Maker application, and the European Environment Agency recommends its usage for European mapping for statistical analysis and display. It is also used in scientific disciplines such as geology for plotting the orientations of lines in three-dimensional space. This plotting is aided by a special kind of graph paper called a Schmidt net.Ramsay (1967) Definition To defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hobo–Dyer Projection
The Hobo–Dyer map projection is a normal cylindrical equal-area projection, with standard parallels (there is no north-south or east-west distortion) at 37.5° north and south of the equator. The map was commissioned in 2002 by Bob Abramms and Howard Bronstein of ODT Inc. and drafted by cartographer Mick Dyer, as a modification of the 1910 Behrmann projection. The name ''Hobo–Dyer'' is derived from Bronstein and Abramms's first names (Howard and Bob) and Dyer's surname. The original ODT map is printed on two sides, one side with north upwards and the other with south upwards. That, together with its equal-area presentation, is intended to present a different perspective compared with more common non-equal area, north-up maps. The goal is similar to that of other equal-area projections (such as the Gall–Peters projection), but the Hobo–Dyer is billed by the publisher as "more visually satisfying". To that end, the map stretches the low latitudes vertically less than Pet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Behrmann Projection
The Behrmann projection is a cylindrical equal-area projection, cylindrical equal-area map projection described by Walter Behrmann in 1910. Cylindrical equal-area projections differ by their standard parallels, which are Parallels of latitude, parallels along which the projection has no distortion. In the case of the Behrmann projection, the standard parallels are 30°N and 30°S. While equal-area, distortion of shape increases in the Behrmann projection according to distance from the standard parallels. The Behrmann projection has the property that half of the Earth's surface is stretched horizontally and the other half is stretched vertically. This projection is not Map projection#Equidistant, equidistant. See also *List of map projections References External links *Table of examples and properties of all common projections from radicalcartography.net Cylindrical equal-area projections {{cartography-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
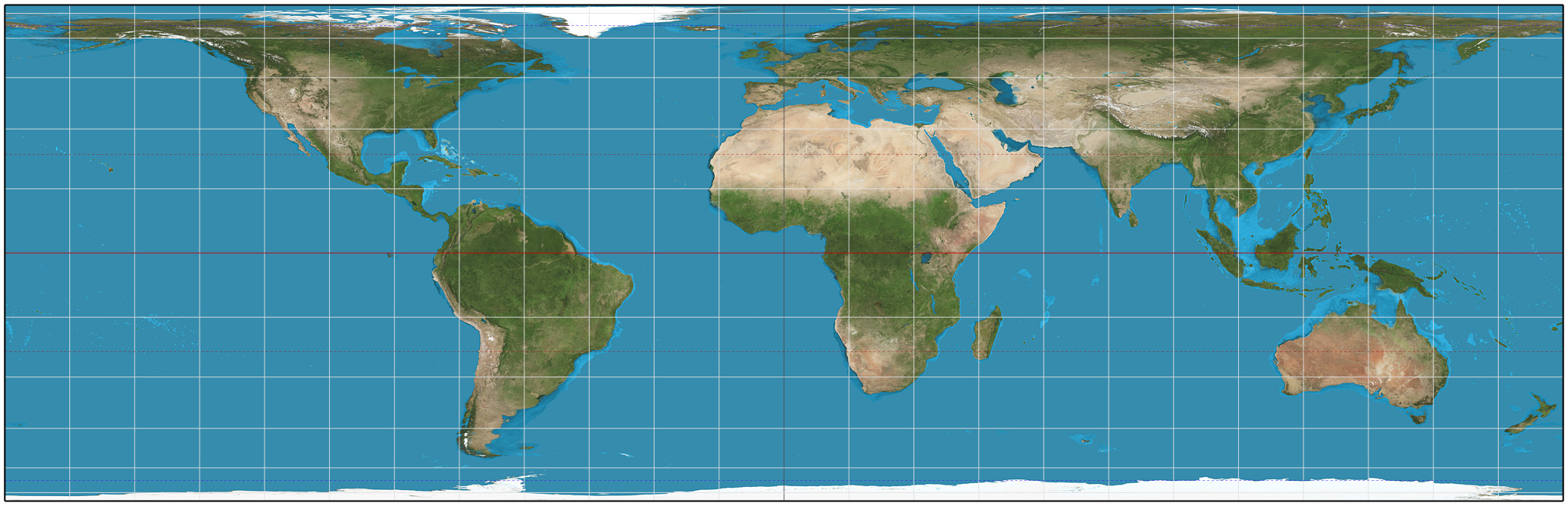
Lambert Cylindrical Equal-area Projection
In cartography, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is a cylindrical equal-area projection. This projection is undistorted along the equator, which is its standard parallel, but distortion increases rapidly towards the poles. Like any cylindrical projection, it stretches parallels increasingly away from the equator. The poles accrue infinite distortion, becoming lines instead of points. History The projection was invented by the Swiss mathematician Johann Heinrich Lambert and described in his 1772 treatise, ''Beiträge zum Gebrauche der Mathematik und deren Anwendung'', part III, section 6: ''Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten'', translated as, ''Notes and Comments on the Composition of Terrestrial and Celestial Maps''. Lambert's projection is the basis for the cylindrical equal-area projection family. Lambert chose the equator as the parallel of no distortion. By multiplying the projection's heig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Cylindrical Equal-area Projection SW
Lambert may refer to People *Lambert (name), a given name and surname * Lambert, Bishop of Ostia (–1130), became Pope Honorius II *Lambert, Margrave of Tuscany (floruit, fl. 929–931), also count and duke of Lucca *Lambert (pianist), stage-name of German pianist and composer Paul Lambert *Johann Heinrich Lambert (1728–1777), polymath Places United States *Lambert, Mississippi, a town *Lambert, Missouri, a village *St. Louis Lambert International Airport, St. Louis, Missouri *Lambert, Montana, a rural town in Montana *Lambert, Oklahoma, a town *Lambert Township, Red Lake County, Minnesota *Lambert Castle, a mansion in Paterson, New Jersey *Lambert Creek, San Mateo County, California Elsewhere *Centre_points_of_Australia#Lambert Gravitational Centre, Lambert Gravitational Centre, the geographical centre of Australia *Lambert (lunar crater), named after Johann Heinrich Lambert *Lambert (Martian crater), named after Johann Heinrich Lambert Transportation *Lambert (automobile), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
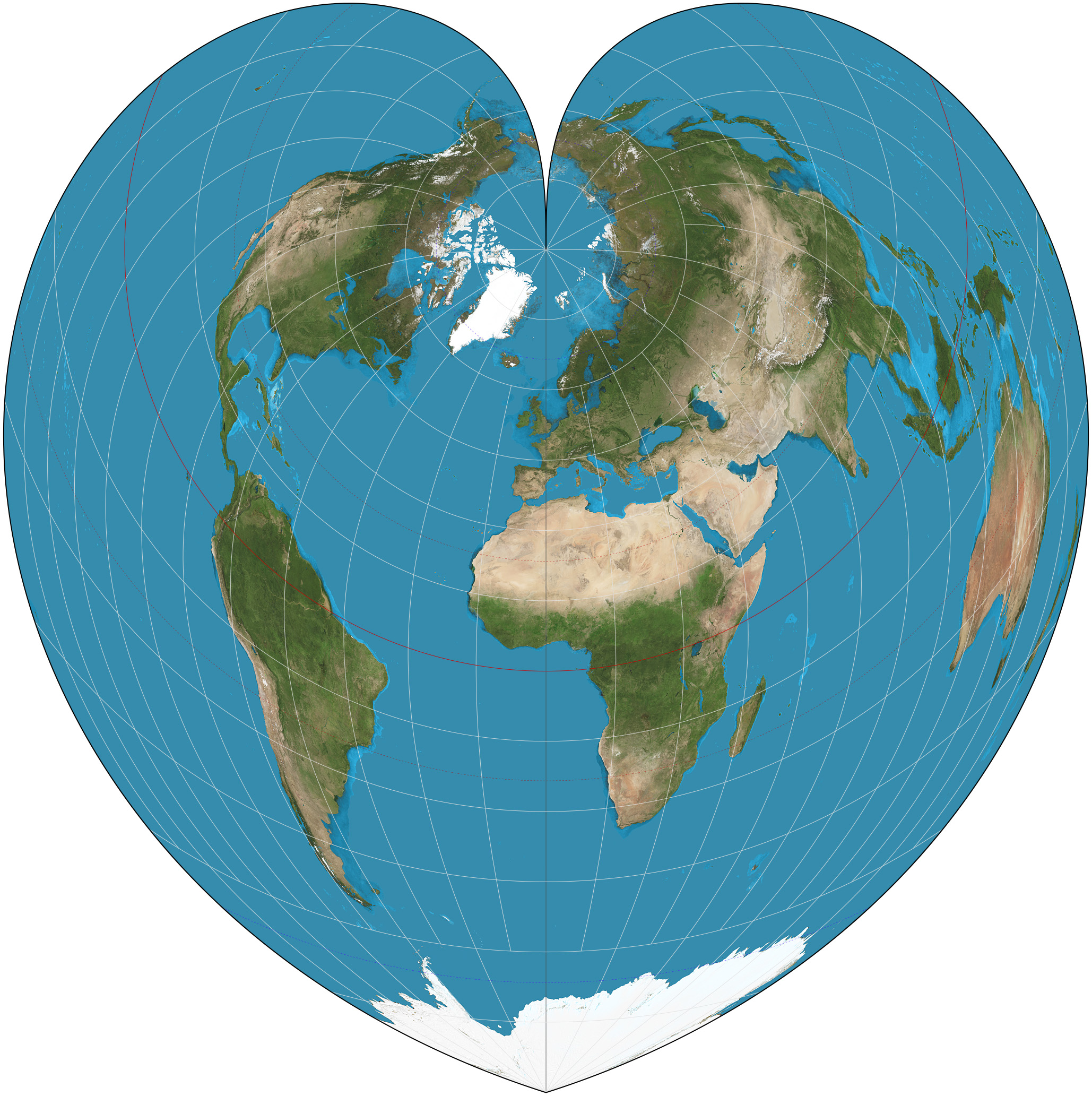
Werner Projection
The Werner projection is a pseudoconic equal-area map projection sometimes called the Stab-Werner or Stabius-Werner projection. Like other heart-shaped projections, it is also categorized as cordiform. ''Stab-Werner'' refers to two originators: Johannes Werner (1466–1528), a parish priest in Nuremberg, refined and promoted this projection that had been developed earlier by Johannes Stabius (Stab) of Vienna Vienna ( ; ; ) is the capital city, capital, List of largest cities in Austria, most populous city, and one of Federal states of Austria, nine federal states of Austria. It is Austria's primate city, with just over two million inhabitants. ... around 1500. The projection is a limiting form of the Bonne projection, having its standard parallel at one of the poles (90°N/S).. Distances along each parallel and along the central meridian are correct, as are all distances from the north pole. See also * List of map projections References External links * *. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bottomley Projection
The Bottomley map projection is a pseudoconical equal area map projection defined as: :x = \frac, \qquad y = \frac - \rho \cos E \, where :\rho = \frac - \varphi, \qquad E = \frac and ''φ'' is the latitude, ''λ'' is the longitude from the central meridian, and ''φ''1 is the given parallel of the projection which determines its shape, all in radians. The inverse projection is then given by: :\begin\varphi &= \frac - \rho \\ \lambda &=\frac \end where :\rho = \sqrt, \qquad E= \tan^\left(\frac\right). Parallels (i.e. lines of latitude) are concentric elliptical arcs of constant eccentricity equal to cos ''φ''1, centred on the North Pole. On the central meridian, shapes are not distorted, but elsewhere they are. Different projections can be produced by altering the eccentricity of the arcs, making it vary between the sinusoidal projection and the Werner projection. For larger values of ''φ''1, it produces a heart shape. It was introduced by Henry Bottomley as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bonne Projection
The Bonne projection is a pseudoconical equal-area map projection, sometimes called a dépôt de la guerre, modified Flamsteed, or a Sylvanus projection. Although named after Rigobert Bonne (1727–1795), the projection was in use prior to his birth, by Sylvanus in 1511, Honter in 1561, De l'Isle before 1700 and Coronelli in 1696. Both Sylvanus and Honter's usages were approximate, however, and it is not clear they intended to be the same projection. The Bonne projection maintains accurate shapes of areas along the central meridian and the standard parallel, but progressively distorts away from those regions. Thus, it best maps "t"-shaped regions. It has been used extensively for maps of Europe and Asia. The projection is defined as: :\begin x &= \rho \sin E \\ y &= \cot \varphi_1 - \rho \cos E\end where :\begin\rho &= \cot \varphi_1 + \varphi_1 - \varphi \\ E &= \frac \end and ''φ'' is the latitude, ''λ'' is the longitude, ''λ''0 is the longitude of the central me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bottomley Projection SW
Bottomley and its homophone Bottomly are English surnames. They come from the placename formed by combining geographic terms " bottom" and " ley", and which refers to two small settlements each on opposite sides of a hill near Walsden and Halifax, West Yorkshire. It first appears in written records from 1277. Notable people with these surnames include: *Arthur Bottomley (1907–1995), British Labour politician *Christine Bottomley (born 1979), English actress *Gordon Bottomley (1874–1948), English poet *Horatio Bottomley (1860–1933), British journalist, newspaper proprietor and fraudster, MP for Hackney South * James Bottomley (diplomat) (1920–2013), British diplomat *James Thomson Bottomley (1845–1926), British physicist *Jim Bottomley (1900–1959), baseball player *John Bottomley, Canadian singer-songwriter *John Bottomly, claimant in Bottomly v. Passamaquoddy Tribe *John Wallace Bottomley (1934–2017), English television presenter, better known as John Noakes * Laura ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Equal-area Conic Projection
Lambert may refer to People *Lambert (name), a given name and surname * Lambert, Bishop of Ostia (–1130), became Pope Honorius II * Lambert, Margrave of Tuscany (fl. 929–931), also count and duke of Lucca *Lambert (pianist), stage-name of German pianist and composer Paul Lambert *Johann Heinrich Lambert (1728–1777), polymath Places United States *Lambert, Mississippi, a town *Lambert, Missouri, a village *St. Louis Lambert International Airport, St. Louis, Missouri * Lambert, Montana, a rural town in Montana *Lambert, Oklahoma, a town * Lambert Township, Red Lake County, Minnesota *Lambert Castle, a mansion in Paterson, New Jersey * Lambert Creek, San Mateo County, California Elsewhere * Lambert Gravitational Centre, the geographical centre of Australia *Lambert (lunar crater), named after Johann Heinrich Lambert * Lambert (Martian crater), named after Johann Heinrich Lambert Transportation *Lambert (automobile), a defunct American automobile brand *Lambert (cyclecar), Bri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |