|
Empirical Bayes Method
Empirical Bayes methods are procedures for statistical inference in which the prior probability distribution is estimated from the data. This approach stands in contrast to standard Bayesian methods, for which the prior distribution is fixed before any data are observed. Despite this difference in perspective, empirical Bayes may be viewed as an approximation to a fully Bayesian treatment of a hierarchical model wherein the parameters at the highest level of the hierarchy are set to their most likely values, instead of being integrated out. Introduction Empirical Bayes methods can be seen as an approximation to a fully Bayesian treatment of a hierarchical Bayes model. In, for example, a two-stage hierarchical Bayes model, observed data y = \ are assumed to be generated from an unobserved set of parameters \theta = \ according to a probability distribution p(y\mid\theta)\,. In turn, the parameters \theta can be considered samples drawn from a population characterised b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Inference
Statistical inference is the process of using data analysis to infer properties of an underlying probability distribution.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for prediction is referred to as ''inference'' (instead of ''prediction''); se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
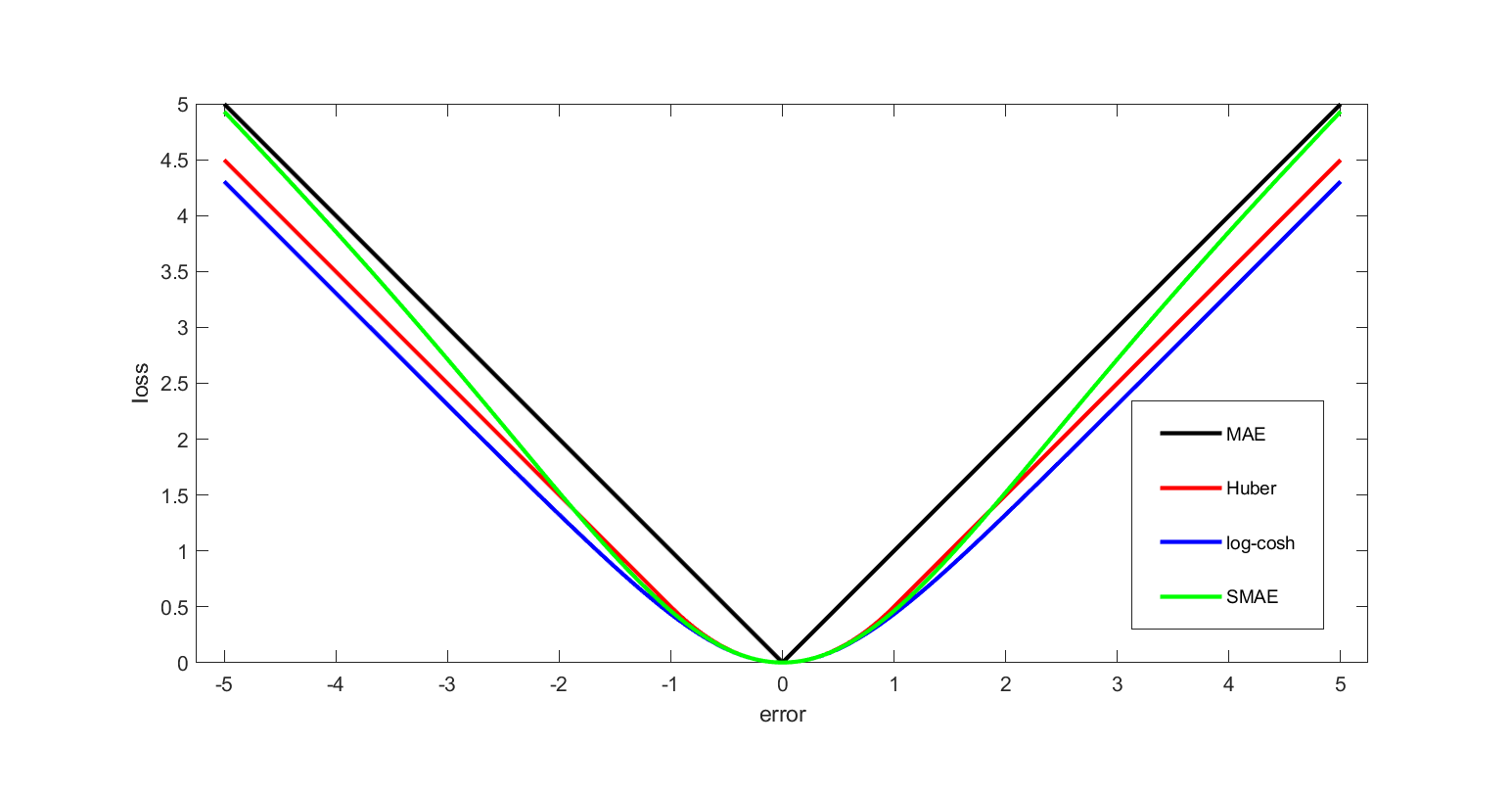
Squared Error Loss
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, this is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta-binomial Model
In probability theory and statistics, the beta-binomial distribution is a family of discrete probability distributions on a finite support of non-negative integers arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. The beta-binomial distribution is the binomial distribution in which the probability of success at each of ''n'' trials is not fixed but randomly drawn from a beta distribution. It is frequently used in Bayesian statistics, empirical Bayes methods and classical statistics to capture overdispersion in binomial type distributed data. The beta-binomial is a one-dimensional version of the Dirichlet-multinomial distribution as the binomial and beta distributions are univariate versions of the multinomial and Dirichlet distributions respectively. The special case where ''α'' and ''β'' are integers is also known as the negative hypergeometric distribution. Motivation and derivation As a compound d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the moments of random variables. Significance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Likelihood Estimate
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when the random errors are assumed to have normal distributions with the same variance. From the perspective of Bayesian inference, ML ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Prior
In Bayesian probability theory, if, given a likelihood function p(x \mid \theta), the posterior distribution p(\theta \mid x) is in the same probability distribution family as the prior probability distribution p(\theta), the prior and posterior are then called conjugate distributions with respect to that likelihood function and the prior is called a conjugate prior for the likelihood function p(x \mid \theta). A conjugate prior is an algebraic convenience, giving a closed-form expression for the posterior; otherwise, numerical integration may be necessary. Further, conjugate priors may clarify how a likelihood function updates a prior distribution. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory.Howard Raiffa and Robert Schlaifer. ''Applied Statistical Decision Theory''. Division of Research, Graduate School of Business Administration, Harvard University, 1961. A similar c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Model
In machine learning, diffusion models, also known as diffusion-based generative models or score-based generative models, are a class of latent variable model, latent variable generative model, generative models. A diffusion model consists of two major components: the forward diffusion process, and the reverse sampling process. The goal of diffusion models is to learn a diffusion process for a given dataset, such that the process can generate new elements that are distributed similarly as the original dataset. A diffusion model models data as generated by a diffusion process, whereby a new datum performs a Wiener process, random walk with drift through the space of all possible data. A trained diffusion model can be sampled in many ways, with different efficiency and quality. There are various equivalent formalisms, including Markov chains, denoising diffusion probabilistic models, noise conditioned score networks, and stochastic differential equations. They are typically trained ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Score (statistics)
In statistics, the score (or informant) is the gradient of the log-likelihood function with respect to the statistical parameter, parameter vector. Evaluated at a particular value of the parameter vector, the score indicates the steepness of the log-likelihood function and thereby the sensitivity to infinitesimal changes to the parameter values. If the log-likelihood function is Continuous function, continuous over the parameter space, the score will vanish (mathematics), vanish at a local Maxima and minima, maximum or minimum; this fact is used in maximum likelihood estimation to find the parameter values that maximize the likelihood function. Since the score is a function of the Realization (probability), observations, which are subject to sampling error, it lends itself to a test statistic known as ''score test'' in which the parameter is held at a particular value. Further, the likelihood ratio, ratio of two likelihood functions evaluated at two distinct parameter values can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value. Definitions Notation and parametrization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shrinkage (statistics)
In statistics, shrinkage is the reduction in the effects of sampling variation. In regression analysis, a fitted relationship appears to perform less well on a new data set than on the data set used for fitting. In particular the value of the coefficient of determination 'shrinks'. This idea is complementary to overfitting and, separately, to the standard adjustment made in the coefficient of determination to compensate for the subjective effects of further sampling, like controlling for the potential of new explanatory terms improving the model by chance: that is, the adjustment formula itself provides "shrinkage." But the adjustment formula yields an artificial shrinkage. A shrinkage estimator is an estimator that, either explicitly or implicitly, incorporates the effects of shrinkage. In loose terms this means that a naive or raw estimate is improved by combining it with other information. The term relates to the notion that the improved estimate is made closer to the value supp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |