|
Elongated Pentagonal Orthobirotunda
In geometry, the elongated pentagonal orthobirotunda is one of the Johnson solids (). Its Conway polyhedron notation iat5jP5 As the name suggests, it can be constructed by elongating a pentagonal orthobirotunda () by inserting a decagonal prism between its congruent halves. Rotating one of the pentagonal rotundae () through 36 degrees before inserting the prism yields the elongated pentagonal gyrobirotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal orthobirotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 26, 2010. :V=\frac\left(45+17\sqrt+15\sqrt\right)a^3\approx21.5297...a^3 :A=\left(10+\sqrt\right)a^2\approx39 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decagonal Prism
In geometry, a prism is a polyhedron comprising an polygon base, a second base which is a translated copy (rigidly moved without rotation) of the first, and other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). Oblique vs right An oblique prism is a prism in which the joining edges and faces are ''not perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stephen Wolfram
Stephen Wolfram ( ; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer algebra and theoretical physics. In 2012, he was named a fellow of the American Mathematical Society. As a businessman, he is the founder and CEO of the software company Wolfram Research, where he works as chief designer of Mathematica and the Wolfram Alpha answer engine. Early life Family Stephen Wolfram was born in London in 1959 to Hugo and Sybil Wolfram, both German Jewish refugees to the United Kingdom. His maternal grandmother was British psychoanalyst Kate Friedlander. Wolfram's father, Hugo Wolfram, was a textile manufacturer and served as managing director of the Lurex Company—makers of the fabric Lurex. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex polygon, convex'' or ''star polygon, star''. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties These properties apply to all regular polygons, whether convex or star polygon, star: *A regular ''n''-sided polygon has rotational symmetry of order ''n''. *All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. *Together with the property of equal-length sides, this implies that every regular polygon also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faces (geometry)
In solid geometry, a face is a flat surface (a Plane (geometry), planar region (mathematics), region) that forms part of the boundary of a solid object. For example, a cube has six faces in this sense. In more modern treatments of the geometry of polyhedra and higher-dimensional polytopes, a "face" is defined in such a way that it may have any dimension. The vertices, edges, and (2-dimensional) faces of a polyhedron are all faces in this more general sense. Polygonal face In elementary geometry, a face is a polygon on the boundary of a polyhedron. (Here a "polygon" should be viewed as including the 2-dimensional region inside it.) Other names for a polygonal face include polyhedron side and Euclidean plane ''tessellation, tile''. For example, any of the six square (geometry), squares that bound a cube is a face of the cube. Sometimes "face" is also used to refer to the 2-dimensional features of a 4-polytope. With this meaning, the 4-dimensional tesseract has 24 square faces, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship between given quantities. The plural of ''formula'' can be either ''formulas'' (from the most common English plural noun form) or, under the influence of scientific Latin, ''formulae'' (from the original Latin). In mathematics In mathematics, a formula generally refers to an equation or inequality relating one mathematical expression to another, with the most important ones being mathematical theorems. For example, determining the volume of a sphere requires a significant amount of integral calculus or its geometrical analogue, the method of exhaustion. However, having done this once in terms of some parameter (the radius for example), mathematicians have produced a formula to describe the volume of a sphere in terms of its radius: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Rotunda
The pentagonal rotunda is a convex polyhedron with regular polygonal faces. These faces comprise ten equilateral triangles, six regular pentagons, and one regular decagon, making a total of seventeen. The pentagonal rotunda is an example of Johnson solid, enumerated as the sixth Johnson solid J_6 . It is another example of a elementary polyhedron because by slicing it with a plane, the resulting smaller convex polyhedra do not have regular faces. The pentagonal rotunda can be regarded as half of an icosidodecahedron, an Archimedean solid, or as half of a pentagonal orthobirotunda, another Johnson solid. Both polyhedrons are constructed by attaching two pentagonal rotundas base-to-base. The difference is one of the pentagonal rotundas is twisted. Other Johnson solids constructed by attaching to the base of a pentagonal rotunda are elongated pentagonal rotunda, gyroelongated pentagonal rotunda, pentagonal orthocupolarotunda, pentagonal gyrocupolarotunda, elongated pentagonal orthoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Orthobirotunda
In geometry, the pentagonal orthobirotunda is a polyhedron constructed by attaching two pentagonal rotundae along their decagonal faces, matching like faces. It is an example of Johnson solid. Construction The pentagonal orthobirotunda is constructed by attaching two pentagonal rotundas to their base, covering decagon faces. The resulting polyhedron has 32 faces, 30 vertices, and 60 edges. This construction is similar to icosidodecahedron (or pentagonal gyrobirotunda), an Archimedean solid: the difference is one of its rotundas twisted around 36°, making the pentagonal faces connect to the triangular one, a process known as gyration. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s .... The pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Pentagonal Gyrocupolarotunda
In geometry, the elongated pentagonal gyrocupolarotunda is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a pentagonal gyrocupolarotunda () by inserting a decagonal prism between its halves. Rotating either the pentagonal cupola () or the pentagonal rotunda () through 36 degrees before inserting the prism yields an elongated pentagonal orthocupolarotunda (). Formulae The following formulae for volume and surface area can be used if all faces are regular, with edge length ''a'':Stephen Wolfram,Elongated pentagonal gyrocupolarotunda from Wolfram Alpha WolframAlpha ( ) is an answer engine developed by Wolfram Research. It is offered as an online service that answers factual queries by computing answers from externally sourced data. History Launch preparations for WolframAlpha began on Ma .... Retrieved July 25, 2010. :V=\frac\left(11+5\sqrt+6\sqrt\right)a^3\approx16.936...a^3 :A=\frac\left(60+\sqrt\right)a^2\approx33.5385 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
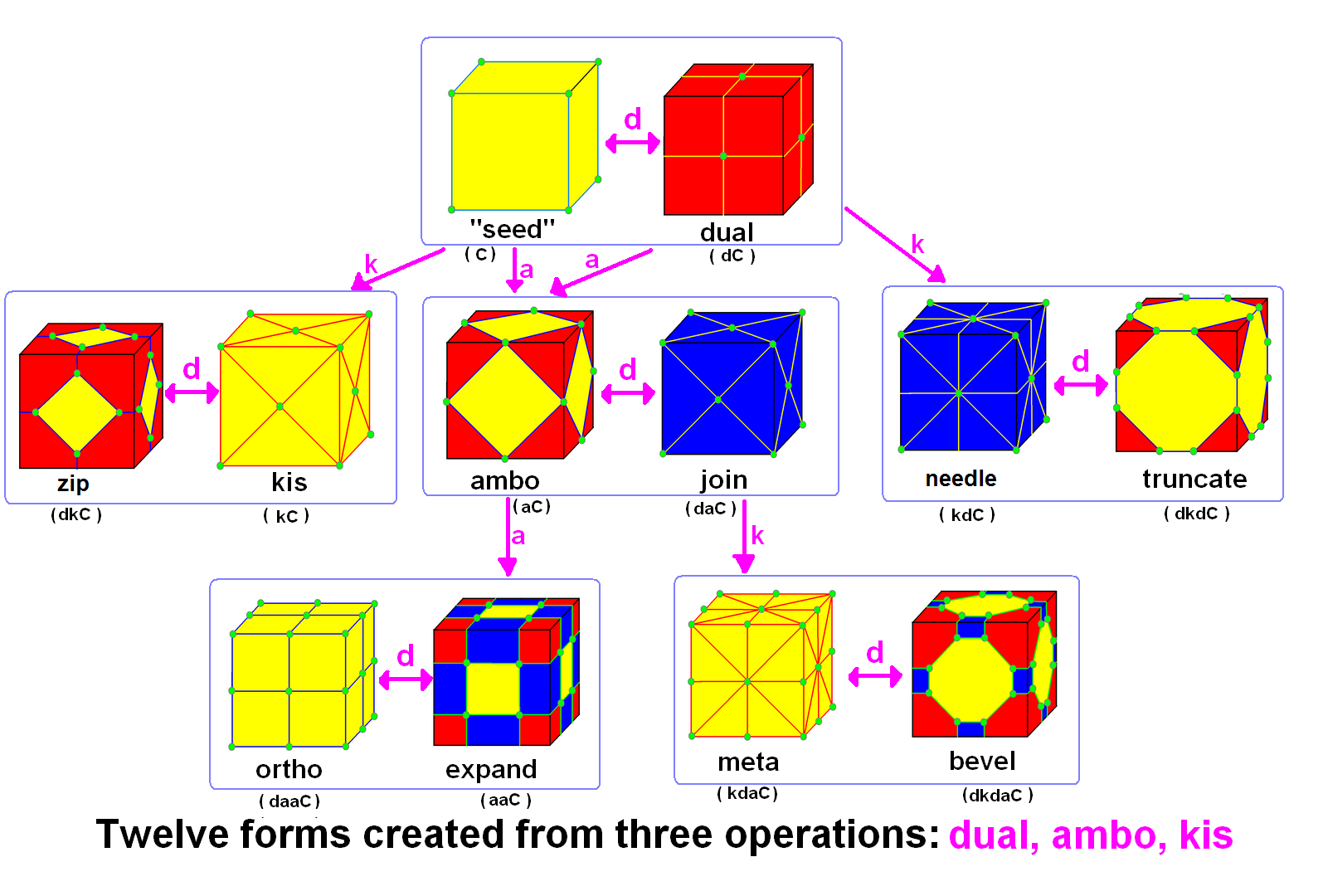
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |