|
Elasticity Of A Function
In mathematics, the elasticity or point elasticity of a positive differentiable function ''f'' of a positive variable (positive input, positive output) at point ''a'' is defined as :Ef(a) = \fracf'(a) :=\lim_\frac\frac=\lim_\frac\frac=\lim_\frac\approx \frac or equivalently :Ef(x) = \frac. It is thus the ratio of the relative (percentage) change in the function's output f(x) with respect to the relative change in its input x, for infinitesimal changes from a point (a, f(a)). Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. Generalizations to multi-input–multi-output cases also exist in the literature. The elasticity of a function is a constant \alpha if and only if the function has the form f(x) = C x ^ \alpha for a constant C>0. The elasticity at a point is the limit of the arc elasticity between two points as the separation between those two points approaches zer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray (geometry)
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word ''line'' may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points (its ''endpoints''). Euclid's ''Elements'' defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. ''Euclidean line'' and ''Euclidean geometry'' are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as non-Euclidean, projective, and affine geometry. Properties In the Greek deductive geometry of Euclid's ''Elements'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function is defined by the formula \frac where is the derivative of . Intuitively, this is the infinitesimal relative change in ; that is, the infinitesimal absolute change in , namely scaled by the current value of . When is a function of a real variable , and takes real, strictly positive values, this is equal to the derivative of , or the natural logarithm of . This follows directly from the chain rule: \frac\ln f(x) = \frac \frac Basic properties Many properties of the real logarithm also apply to the logarithmic derivative, even when the function does ''not'' take values in the positive reals. For example, since the logarithm of a product is the sum of the logarithms of the factors, we have (\log uv)' = (\log u + \log v)' = (\log u)' + (\log v)' . So for positive-real-valued functions, the logarithmic derivative of a product is the sum of the logarithmic derivatives ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Function
In mathematics, a homogeneous function is a function of several variables such that the following holds: If each of the function's arguments is multiplied by the same scalar (mathematics), scalar, then the function's value is multiplied by some power of this scalar; the power is called the degree of homogeneity, or simply the ''degree''. That is, if is an integer, a function of variables is homogeneous of degree if :f(sx_1,\ldots, sx_n)=s^k f(x_1,\ldots, x_n) for every x_1, \ldots, x_n, and s\ne 0. This is also referred to a ''th-degree'' or ''th-order'' homogeneous function. For example, a homogeneous polynomial of degree defines a homogeneous function of degree . The above definition extends to functions whose domain of a function, domain and codomain are vector spaces over a Field (mathematics), field : a function f : V \to W between two -vector spaces is ''homogeneous'' of degree k if for all nonzero s \in F and v \in V. This definition is often further generalized to f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Coefficient
In chemistry, the Reaction rate, rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant, the concentration of Product (chemistry), products, and other effectors. The degree to which these factors change the reaction rate is described by the elasticity coefficient. This coefficient is defined as follows: \varepsilon_^v = \left(\frac \frac\right)_ = \frac \approx \frac where v denotes the reaction rate and s denotes the Substrate (chemistry), substrate concentration. Be aware that the notation will use lowercase roman letters, such as s, to indicate concentrations. The partial derivative in the definition indicates that the elasticity is measured with respect to changes in a factor S while keeping all other factors constant. The most common factors include substrates, products, enzyme, and effectors. The scaling of the coefficient ensures that it is dimensionless and independent of the units used to measure the reaction rate and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
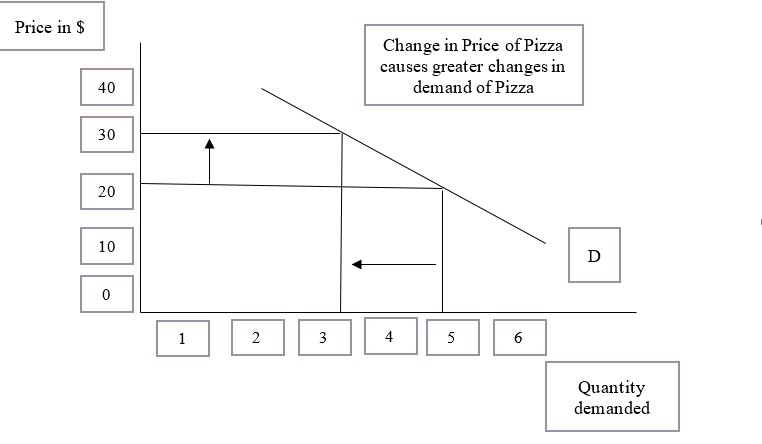
Elasticity (economics)
In economics, elasticity measures the responsiveness of one economic variable to a change in another. For example, if the price elasticity of the demand of a good is −2, then a 10% increase in price will cause the quantity demanded to fall by 20%. Elasticity in economics provides an understanding of changes in the behavior of the buyers and sellers with price changes. There are two types of elasticity for demand and supply, one is inelastic demand and supply and the other one is elastic demand and supply. Introduction The concept of price elasticity was first cited in an informal form in the book ''Principles of Economics (Marshall book), Principles of Economics'' published by the author Alfred Marshall in 1890. Subsequently, a major study of the price elasticity of supply and the price elasticity of demand for US products was undertaken by Joshua Levy and Trevor Pollock in the late 1960s. Elasticity is an important concept in neoclassical economic theory, and enables in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Elasticity
In mathematics and economics, the arc elasticity is the elasticity of one variable with respect to another between two given points. It is the ratio of the percentage change of one of the variables between the two points to the percentage change of the other variable. It contrasts with the ''point elasticity'', which is the limit of the arc elasticity as the distance between the two points approaches zero and which hence is defined at a single point rather than for a pair of points. Formula The ''y'' arc elasticity of ''x'' is defined as: :E_ = \frac where the percentage change in going from point 1 to point 2 is usually calculated relative to the midpoint: :\% \mbox x = \frac; :\% \mbox y = \frac. The use of the midpoint arc elasticity formula (with the midpoint used for the base of the change, rather than the initial point (''x''1, ''y''1) which is used in almost all other contexts for calculating percentages) was advocated by R. G. D. Allen for use when ''x'' refers to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Duration
{{disambiguation ...
Modified may refer to: * ''Modified'' (album), the second full-length album by Save Ferris *Modified racing, or "Modifieds", an American automobile racing genre See also * Modification (other) * Modifier (other) Modifier may refer to: * Grammatical modifier, a word that modifies the meaning of another word or limits its meaning ** Compound modifier, two or more words that modify a noun ** Dangling modifier, a word or phrase that modifies a clause in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supply Function
In economics, supply is the amount of a resource that firms, producers, labourers, providers of financial assets, or other economic agents are willing and able to provide to the marketplace or to an individual. Supply can be in produced goods, labour time, raw materials, or any other scarce or valuable object. Supply is often plotted graphically as a supply curve, with the price per unit on the vertical axis and quantity supplied as a function of price on the horizontal axis. This reversal of the usual position of the dependent variable and the independent variable is an unfortunate but standard convention. The supply curve can be either for an individual seller or for the market as a whole, adding up the quantity supplied by all sellers. The quantity supplied is for a particular time period (e.g., the tons of steel a firm would supply in a year), but the units and time are often omitted in theoretical presentations. In the goods market, supply is the amount of a product per u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marginal Concepts
In economics, marginal concepts are associated with a ''specific change'' in the quantity used of a good or service, as opposed to some notion of the over-all significance of that class of good or service, or of some total quantity thereof.{{citation needed, date=February 2012 Marginality Constraints are conceptualized as a ''border'' or ''margin''. Wicksteed, Philip Henry; ''The Common Sense of Political Economy'' (1910), Bk I Ch 2 and elsewhere. The location of the margin for any individual corresponds to his or her ''endowment'', broadly conceived to include opportunities. This endowment is determined by many things including physical laws (which constrain how forms of energy and matter may be transformed), accidents of nature (which determine the presence of natural resources), and the outcomes of past decisions made both by others and by the individual himself or herself. A value that holds true given particular constraints is a ''marginal'' value. A change that would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Function
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Demand Function
In economics, an inverse demand function is the mathematical relationship that expresses price as a function of quantity demanded (it is therefore also known as a price function). Historically, the economists first expressed the price of a good as a function of demand (holding the other economic variables, like income, constant), and plotted the price-demand relationship with demand on the x (horizontal) axis (the demand curve). Later the additional variables, like prices of other goods, came into analysis, and it became more convenient to express the demand as a multivariate function (the demand function): = f(, , ...), so the original demand curve now depicts the ''inverse'' demand function = f^() with extra variables fixed. Definition In mathematical terms, if the demand function is = f(), then the inverse demand function is = f^(). The value of the inverse demand function is the highest price that could be charged and still generate the quantity demanded. This is useful ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |