|
Eigenspinor
In quantum mechanics, eigenspinors are basis vectors representing the general spin state of a particle. For a single spin 1/2 particle, they can be defined as the eigenvectors of the Pauli matrices. As such, they are vectors mathematically but physics convention distinguishes vectors from spinors by their transformation behavior. General eigenspinors In quantum mechanics, the spin of a particle or collection of particles is quantized. In particular, all particles have either half integer or integer spin. In the most general case, the eigenspinors for a system can be quite complicated. If you have a collection of the Avogadro number of particles, each one with two (or more) possible spin states, writing down a complete set of eigenspinors would not be practically possible. However, eigenspinors are very useful when dealing with the spins of a very small number of particles. The spin 1/2 particle The simplest and most illuminating example of eigenspinors is for a single spin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spinor
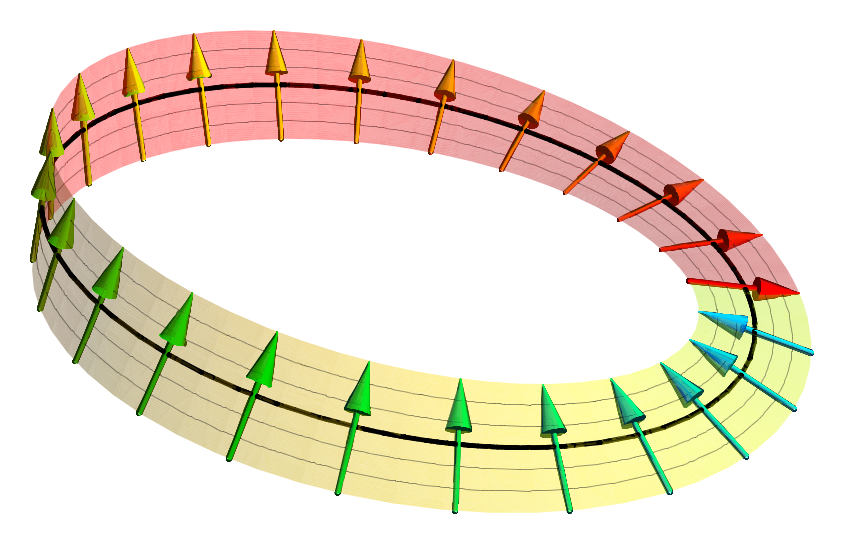
In geometry and physics, spinors (pronounced "spinner" IPA ) are elements of a complex numbers, complex vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal transformation, infinitesimal) rotation, but unlike Euclidean vector, geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of Section (fiber bundle), sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction (geometry), direction and a magnitude, and both are conserved. Bicycle and motorcycle dynamics, Bicycles and motorcycles, flying discs, Rifling, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis (linear Algebra)
In mathematics, a Set (mathematics), set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension (vector space), dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frame of reference, frames of reference. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Combination
In mathematics, a linear combination or superposition is an Expression (mathematics), expression constructed from a Set (mathematics), set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' and ''y'' would be any expression of the form ''ax'' + ''by'', where ''a'' and ''b'' are constants). The concept of linear combinations is central to linear algebra and related fields of mathematics. Most of this article deals with linear combinations in the context of a vector space over a field (mathematics), field, with some generalizations given at the end of the article. Definition Let ''V'' be a vector space over the field ''K''. As usual, we call elements of ''V'' ''vector space, vectors'' and call elements of ''K'' ''scalar (mathematics), scalars''. If v1,...,v''n'' are vectors and ''a''1,...,''a''''n'' are scalars, then the ''linear combination of those vectors with those scalars as coefficients'' is :a_1 \mathbf v_1 + a_2 \mathbf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal Basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space V with finite Dimension (linear algebra), dimension is a Basis (linear algebra), basis for V whose vectors are orthonormal, that is, they are all unit vectors and Orthogonality_(mathematics), orthogonal to each other. For example, the standard basis for a Euclidean space \R^n is an orthonormal basis, where the relevant inner product is the dot product of vectors. The Image (mathematics), image of the standard basis under a Rotation (mathematics), rotation or Reflection (mathematics), reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for \R^n arises in this fashion. An orthonormal basis can be derived from an orthogonal basis via Normalize (linear algebra), normalization. The choice of an origin (mathematics), origin and an orthonormal basis forms a coordinate frame known as an ''orthonormal frame''. For a general inner product space V, an orthono ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in . Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. \sqrt is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it (see further examples below). It is always possible to "fill all the holes", leading to the ''completion'' of a given space, as explained below. Definition Cauchy sequence A sequence x_1, x_2, x_3, \ldots of elements from X of a metric space (X, d) is called Cauchy if for every positive real number r > 0 there is a positive integer N such that for all positive integers m, n > N, d(x_m, x_n) < r. Complete space A metric space is complete if any of the following equivalent conditions are satisfied: #Every Cauchy se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3D Spherical
3D, 3-D, 3d, or Three D may refer to: Science, technology, and mathematics * A three-dimensional space in mathematics Relating to three-dimensionality * 3D computer graphics, computer graphics that use a three-dimensional representation of geometric data * 3D display, a type of information display that conveys depth to the viewer * 3D film, a motion picture that gives the illusion of three-dimensional perception * 3D modeling, developing a representation of any three-dimensional surface or object * 3D printing, making a three-dimensional solid object of a shape from a digital model * 3D television, television that conveys depth perception to the viewer * 3D projection * 3D rendering * 3D scanning, making a digital representation of three-dimensional objects * Video game graphics#3D, 3D video game * Stereoscopy, any technique capable of recording three-dimensional visual information or creating the illusion of depth in an image * Three-dimensional space Other uses in science and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called '' 3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a '' solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenstates
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for time i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis Vector
In mathematics, a set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components or coordinates of the vector with respect to . The elements of a basis are called . Equivalently, a set is a basis if its elements are linearly independent and every element of is a linear combination of elements of . In other words, a basis is a linearly independent spanning set. A vector space can have several bases; however all the bases have the same number of elements, called the dimension of the vector space. This article deals mainly with finite-dimensional vector spaces. However, many of the principles are also valid for infinite-dimensional vector spaces. Basis vectors find applications in the study of crystal structures and frames of reference. Definition A basis of a vector space over a field (such as th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |