|
Edwin E. Moise
Edwin Evariste Moise (; December 22, 1918 – December 18, 1998) was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th-century English poetry and had several notes published in that field. Early life and education Edwin E. Moise was born December 22, 1918, in New Orleans, Louisiana. He graduated from Tulane University in 1940. He worked as a cryptanalyst and Japanese translator for the Office of the Chief of Naval Operations during World War II. He received his Ph.D. degree in mathematics from the University of Texas in 1947. His dissertation was titled "An indecomposable continuum which is homeomorphic to each of its nondegenerate subcontinua," a topic in continuum theory, and was written under the direction of Robert Lee Moore. In his dissertation Moise coined the term pseudo-arc. Career Moise taught at the University of Michigan from 1947 to 1960. He was James B. Conant P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New Orleans
New Orleans (commonly known as NOLA or The Big Easy among other nicknames) is a Consolidated city-county, consolidated city-parish located along the Mississippi River in the U.S. state of Louisiana. With a population of 383,997 at the 2020 United States census, 2020 census, it is the List of municipalities in Louisiana, most populous city in Louisiana and the French Louisiana region, the second-most populous in the Deep South, and the twelfth-most populous in the Southeastern United States. The city is coextensive with Orleans Parish, Louisiana, Orleans Parish. New Orleans serves as a major port and a commercial hub for the broader Gulf Coast of the United States, Gulf Coast region. The New Orleans metropolitan area has a population of approximately 1 million, making it the most populous metropolitan area in Louisiana and the List of metropolitan statistical areas, 59th-most populous in the United States. New Orleans is world-renowned for Music of New Orleans, its distincti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Notices Of The American Mathematical Society
''Notices of the American Mathematical Society'' is the membership journal of the American Mathematical Society (AMS), published monthly except for the combined June/July issue. The first volume was published in 1953. Each issue of the magazine since January 1995 is available in its entirety on the journal web site. Articles are peer-reviewed by an editorial board of mathematical experts. Beginning with the January 2025 issue, the editor-in-chief is Mark C. Wilson, succeeding past editor Erica Flapan. The cover regularly features mathematical visualizations. The ''Notices'' is self-described to be the world's most widely read mathematical journal. As the membership journal of the American Mathematical Society, the ''Notices'' is sent to the approximately 30,000 AMS members worldwide, one-third of whom reside outside the United States. By publishing high-level exposition, the ''Notices'' provides opportunities for mathematicians to find out what is going on in the field. Each is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Association Of America
The Mathematical Association of America (MAA) is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university A university () is an educational institution, institution of tertiary education and research which awards academic degrees in several Discipline (academia), academic disciplines. ''University'' is derived from the Latin phrase , which roughly ..., college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists; statisticians; and many others in academia, government, business, and industry. The MAA was founded in 1915 and is headquartered at 11 Dupont in the Dupont Circle, Washington, D.C., Dupont Circle neighborhood of Washington, D.C. The organization publishes mathematics journals and books, including the ''American Mathematical Monthly'' (established in 1894 by Benjamin Finkel), the most widely read mathematics journal in the world according to re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morris Kline
Morris Kline (May 1, 1908 – June 10, 1992) was a professor of mathematics, a writer on the history, philosophy, and teaching of mathematics, and also a popularizer of mathematical subjects. Education and career Kline was born to a Jewish family in Brooklyn and resided in Jamaica, Queens. After graduating from Boys High School in Brooklyn, he studied mathematics at New York University, earning a bachelor's degree in 1930, a master's degree in 1932, and a doctorate (Ph.D.) in 1936. He continued at NYU as an instructor until 1942. During World War II, Kline was posted to the Signal Corps (United States Army) stationed at Belmar, New Jersey. Designated as a physicist, he worked in the engineering lab where radar was developed. After the war, he continued investigating electromagnetism, and from 1946 to 1966, he was director of the division for electromagnetic research at the Courant Institute of Mathematical Sciences. Kline resumed his mathematical teaching at NYU, becoming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saunders Mac Lane
Saunders Mac Lane (August 4, 1909 – April 14, 2005), born Leslie Saunders MacLane, was an American mathematician who co-founded category theory with Samuel Eilenberg. Early life and education Mac Lane was born in Norwich, Connecticut, near where his family lived in Taftville, Connecticut, Taftville.. He was christened "Leslie Saunders MacLane", but "Leslie" fell into disuse because his parents, Donald MacLane and Winifred Saunders, came to dislike it. He began inserting a space into his surname because his first wife found it difficult to type the name without a space. He was the eldest of three brothers; one of his brothers, Gerald MacLane, also became a mathematics professor at Rice University and Purdue University. Another sister died as a baby. His father and grandfather were both ministers; his grandfather had been a Presbyterian, but was kicked out of the church for believing in evolution, and his father was a Congregational church, Congregationalist. His mother, Winifre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangulation (topology)
In mathematics, triangulation describes the replacement of topological spaces with simplicial complexes by the choice of an appropriate homeomorphism. A space that admits such a homeomorphism is called a triangulable space. Triangulations can also be used to define a piecewise linear structure for a space, if one exists. Triangulation has various applications both in and outside of mathematics, for instance in algebraic topology, in complex analysis, and in modeling. Motivation On the one hand, it is sometimes useful to forget about superfluous information of topological spaces: The replacement of the original spaces with simplicial complexes may help to recognize crucial properties and to gain a better understanding of the considered object. On the other hand, simplicial complexes are objects of combinatorial character and therefore one can assign them quantities arising from their combinatorial pattern, for instance, the Euler characteristic. Triangulation allows now to as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-manifold
In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane (geometry), plane (a tangent plane) to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below. Principles Definition A topological space M is a 3-manifold if it is a second-countable Hausdorff space and if every point in M has a neighbourhood (mathematics), neighbourhood that is homeomorphic to Euclidean 3-space. Mathematical theory of 3-manifolds The topological, Piecewise linear manifold, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds. Phenomena in three dimensions can be strikingly different from phenomena in other dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
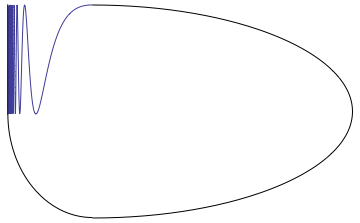
Pseudo-arc
In general topology, the pseudo-arc is the simplest nondegenerate hereditarily indecomposable continuum. The pseudo-arc is an arc-like homogeneous continuum, and played a central role in the classification of homogeneous planar continua. R. H. Bing proved that, in a certain well-defined sense, most continua in , are homeomorphic to the pseudo-arc. History In 1920, Bronisław Knaster and Kazimierz Kuratowski asked whether a nondegenerate homogeneous continuum in the Euclidean plane must be a Jordan curve. In 1921, Stefan Mazurkiewicz asked whether a nondegenerate continuum in that is homeomorphic to each of its nondegenerate subcontinua must be an arc. In 1922, Knaster discovered the first example of a hereditarily indecomposable continuum , later named the pseudo-arc, giving a negative answer to a Mazurkiewicz question. In 1948, R. H. Bing proved that Knaster's continuum is homogeneous, i.e. for any two of its points there is a homeomorphism taking one to the other. Yet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuum Theory
In the mathematical field of point-set topology, a continuum (plural: "continua") is a nonempty compact connected metric space, or, less frequently, a compact connected Hausdorff space. Continuum theory is the branch of topology devoted to the study of continua. Definitions * A continuum that contains more than one point is called nondegenerate. * A subset ''A'' of a continuum ''X'' such that ''A'' itself is a continuum is called a subcontinuum of ''X''. A space homeomorphic to a subcontinuum of the Euclidean plane R2 is called a planar continuum. * A continuum ''X'' is homogeneous if for every two points ''x'' and ''y'' in ''X'', there exists a homeomorphism ''h'': ''X'' → ''X'' such that ''h''(''x'') = ''y''. * A Peano continuum is a continuum that is locally connected at each point. * An indecomposable continuum is a continuum that cannot be represented as the union of two proper subcontinua. A continuum ''X'' is hereditarily indecomposable if every subcontinuum of ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
World War II
World War II or the Second World War (1 September 1939 – 2 September 1945) was a World war, global conflict between two coalitions: the Allies of World War II, Allies and the Axis powers. World War II by country, Nearly all of the world's countries participated, with many nations mobilising all resources in pursuit of total war. Tanks in World War II, Tanks and Air warfare of World War II, aircraft played major roles, enabling the strategic bombing of cities and delivery of the Atomic bombings of Hiroshima and Nagasaki, first and only nuclear weapons ever used in war. World War II is the List of wars by death toll, deadliest conflict in history, causing World War II casualties, the death of 70 to 85 million people, more than half of whom were civilians. Millions died in genocides, including the Holocaust, and by massacres, starvation, and disease. After the Allied victory, Allied-occupied Germany, Germany, Allied-occupied Austria, Austria, Occupation of Japan, Japan, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |