|
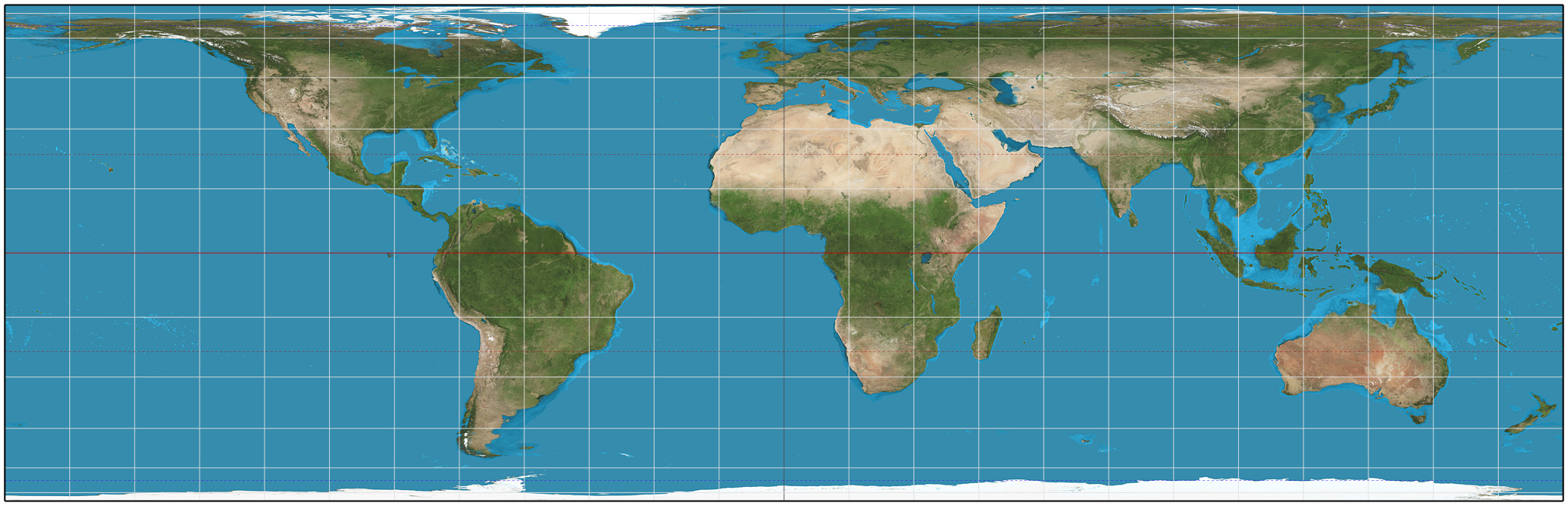
Eckert II Projection
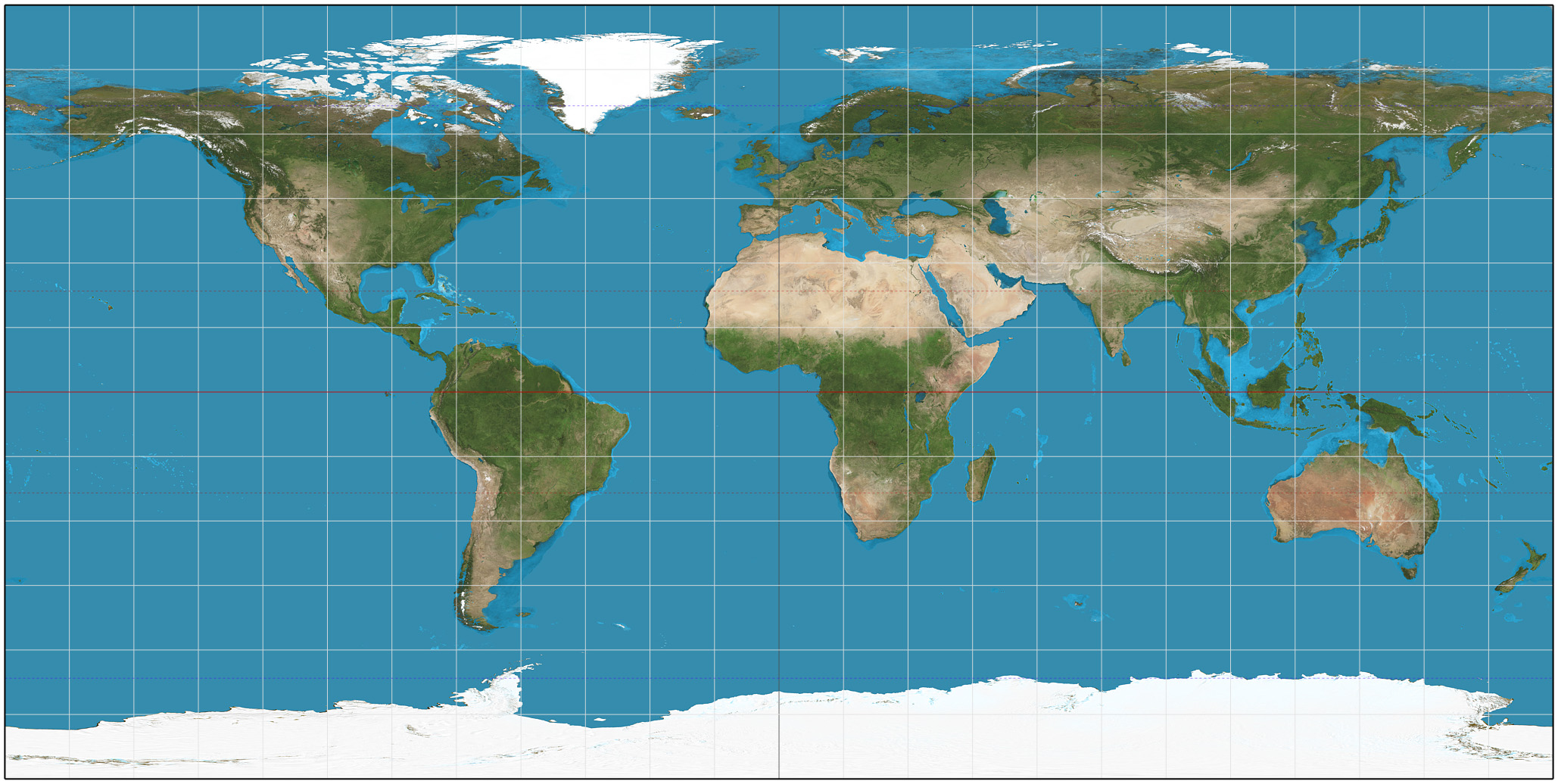
The Eckert II projection is an equal-area pseudocylindrical map projection. In the equatorial aspect (where the equator is shown as the horizontal axis) the network of longitude and latitude lines consists solely of straight lines, and the outer boundary has the distinctive shape of an elongated hexagon. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, the meridians have the same shape, and the odd-numbered projection has equally spaced parallels, whereas the even-numbered projection has parallels spaced to preserve area. The pair to Eckert II is the Eckert I projection. Description The projection is symmetrical about the straight equator and straight central meridian. Parallels vary in spacing in order to preserve areas. As a pseudocylindric projection, spacing of meridians along any given parallel is constant. The poles are represented as lines, each half as long as the equator. The projecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckert II Projection SW
Eckert may refer to: People * Allan W. Eckert (1931–2011), American historical novelist * Andrea Eckert (born 1958), Austrian actress * Charles R. Eckert (1868–1959), U.S. congressman from Pennsylvania * Ernst R. G. Eckert (1904–2004), German scientist ** Eckert number, dimensionless number used in flow calculations * Eugen Eckert (born 1954) German minister, singer-songwriter and academic teacher * Franz Eckert (1852–1916), German musician * Fred J. Eckert (born 1941), U.S. congressman from New York * Fritz Eckert (1852–1920), Swedish architect * George Nicholas Eckert (1802–1865), U.S. congressman from Pennsylvania * John Eckert (musician) (born 1939), American trumpeter * J. Presper Eckert (1919–1995), American electrical engineer, co-inventor of ENIAC ** Eckert–Mauchly Computer Corporation ** Eckert–Mauchly Award * Max Eckert-Greifendorff (1868–1938), German geographer ** Eckert projection, any of six map projections devised by Eckert-Greifendorff * Karl Anto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal-area Projection
In cartography, an equal-area projection is a map projection that preserves area measure, generally distorting shapes in order to do that. Equal-area maps are also called equivalent or authalic. An equal-area map projection cannot be conformal, nor can a conformal map projection be equal-area. Several equivalent projections were developed in an attempt to minimize the distortion of countries and continents of planet Earth, keeping the area constant. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, etc. Description Equal area representation implies that a region of interest in a particular portion of the map will share the same proportion of area as in any other part of the map. Statistical grid The term "statistical grid" refers to a discrete grid (global or local) of an equal-area surface representation, used for data visualization, geocode and statistical spatial analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudocylindrical
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A ''regular hexagon'' has Schläfli symbol and can also be constructed as a truncated equilateral triangle, t, which alternates two types of edges. A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has six rotational symmetries (''rotational symmetry of order six'') and six reflection symmetries (''six lines of symmetry''), making up the dihedral group D6. The longest diagonals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Eckert-Greifendorff
Max Eckert (after 1934, Max Eckert-Greifendorff: 10 April 1868 in Chemnitz, Kingdom of Saxony – 26 December 1938, in Aachen) was a German geographer. Biography He received his education in Löbau and Berlin, and taught for some time at Löbau and Leipzig. In 1903, he became Privatdozent at Kiel University. In 1907, he was appointed to the chair of geography in the Royal Technical High School of Aachen (Aix-la-Chapelle). He invented the six Eckert projections and others such as Eckert-Greifendorff projection Writings He has published ''Schulatlas'' (School atlas, 45th ed., 1912), ''Wesen und Aufgabe der Wirtschafts- und Verkehrsgeographie'' (Essentials and purpose of economic and transportation geography, 1903), ''Grundriss der Handelsgeographie'' (Fundamentals of the geography of trade, 1905), ''Leitfaden der Handelsgeographie'' (Primer of the geography of trade, 3d ed., 1911), ''Neue Entwürfe für Erdkarten'' (New ideas for world maps, 1906), ''Die Kartographie als Wissen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckert I Projection
Eckert may refer to: People * Allan W. Eckert (1931–2011), American historical novelist * Andrea Eckert (born 1958), Austrian actress * Charles R. Eckert (1868–1959), U.S. congressman from Pennsylvania * Ernst R. G. Eckert (1904–2004), German scientist ** Eckert number, dimensionless number used in flow calculations * Eugen Eckert (born 1954) German minister, singer-songwriter and academic teacher * Franz Eckert (1852–1916), German musician * Fred J. Eckert (born 1941), U.S. congressman from New York * Fritz Eckert (1852–1920), Swedish architect * George Nicholas Eckert (1802–1865), U.S. congressman from Pennsylvania * John Eckert (musician) (born 1939), American trumpeter * J. Presper Eckert (1919–1995), American electrical engineer, co-inventor of ENIAC ** Eckert–Mauchly Computer Corporation ** Eckert–Mauchly Award * Max Eckert-Greifendorff (1868–1938), German geographer ** Eckert projection, any of six map projections devised by Eckert-Greifendorff * Karl A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can also be used for any other celestial body that is roughly spherical. In spatial (3D) geometry, as applied in astronomy, the equator of a rotating spheroid (such as a planet) is the parallel (circle of latitude) at which latitude is defined to be 0°. It is an imaginary line on the spheroid, equidistant from its poles, dividing it into northern and southern hemispheres. In other words, it is the intersection of the spheroid with the plane perpendicular to its axis of rotation and midway between its geographical poles. On and near the equator (on Earth), noontime sunlight appears almost directly overhead (no more than about 23° from the zenith) every day, year-round. Consequently, the equator has a rather stable daytime temperature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian (geography)
In geography and geodesy, a meridian is the locus connecting points of equal longitude, which is the angle (in degrees or other units) east or west of a given prime meridian (currently, the IERS Reference Meridian). In other words, it is a line of longitude. The position of a point along the meridian is given by that longitude and its latitude, measured in angular degrees north or south of the Equator. On a Mercator projection or on a Gall-Peters projection, each meridian is perpendicular to all circles of latitude. A meridian is half of a great circle on Earth's surface. The length of a meridian on a modern ellipsoid model of Earth ( WGS 84) has been estimated as . Pre-Greenwich The first prime meridian was set by Eratosthenes in 200 BCE. This prime meridian was used to provide measurement of the earth, but had many problems because of the lack of latitude measurement. Many years later around the 19th century there were still concerns of the prime meridian. Multiple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of Latitude
A circle of latitude or line of latitude on Earth is an abstract east–west small circle connecting all locations around Earth (ignoring elevation) at a given latitude coordinate line. Circles of latitude are often called parallels because they are parallel to each other; that is, planes that contain any of these circles never intersect each other. A location's position along a circle of latitude is given by its longitude. Circles of latitude are unlike circles of longitude, which are all great circles with the centre of Earth in the middle, as the circles of latitude get smaller as the distance from the Equator increases. Their length can be calculated by a common sine or cosine function. The 60th parallel north or south is half as long as the Equator (disregarding Earth's minor flattening by 0.335%). On the Mercator projection or on the Gall-Peters projection, a circle of latitude is perpendicular to all meridians. On the ellipsoid or on spherical projection, all circle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable Notability is the property of being worthy of notice, having fame, or being considered to be of a high degree of interest, significance, or distinction. It also refers to the capacity to be such. Persons who are notable due to public responsibi .... Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection ; Cylindrical: In standard presentation, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In standard presentation, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In standard presentation, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckert IV Projection
The Eckert IV projection is an equal-area pseudocylindrical map projection. The length of the polar lines is half that of the equator, and lines of longitude are semiellipses, or portions of ellipses. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, meridians are the same whereas parallels differ. Odd-numbered projections have parallels spaced equally, whereas even-numbered projections have parallels spaced to preserve area. Eckert IV is paired with Eckert III. Formulas Forward formulae Given a sphere of radius ''R'', central meridian ''λ'' and a point with geographical latitude ''φ'' and longitude ''λ'', plane coordinates ''x'' and ''y'' can be computed using the following formulas: : \begin x & = \frac R\, (\lambda - \lambda_0)(1 + \cos \theta) \approx 0.422\,2382\, R\, (\lambda - \lambda_0)(1 + \cos \theta), \\ pty & = 2 \sqrt R \sin \theta \approx 1.326\,5004\, R \sin \theta, \end where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |