|
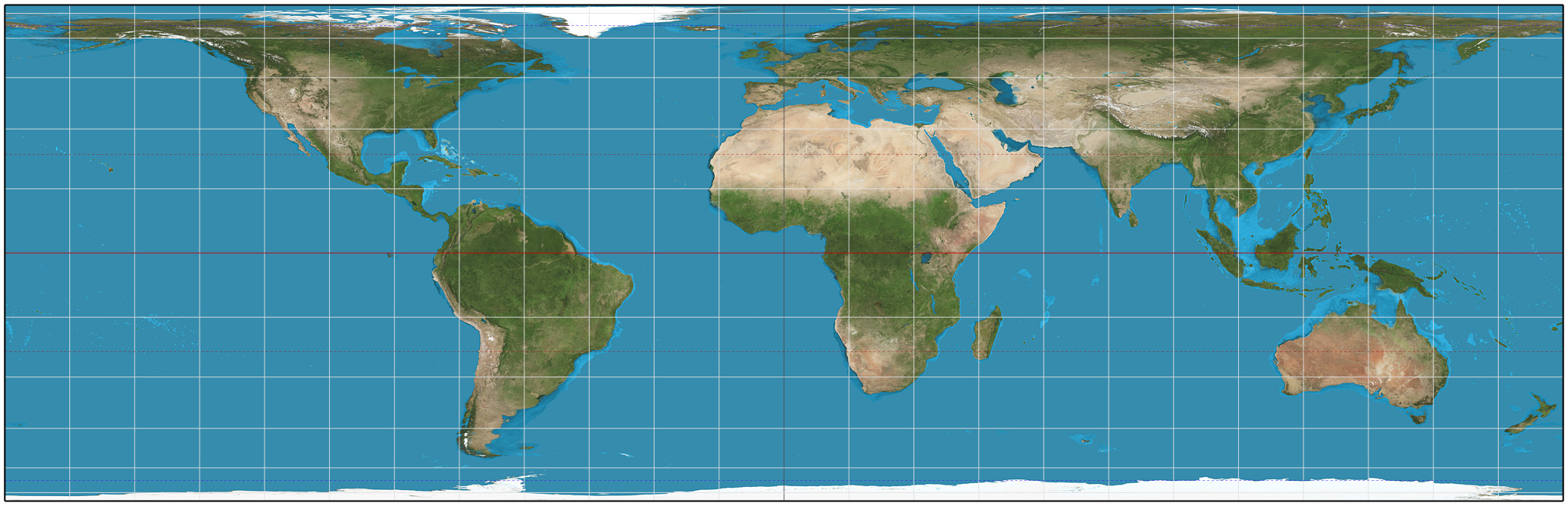
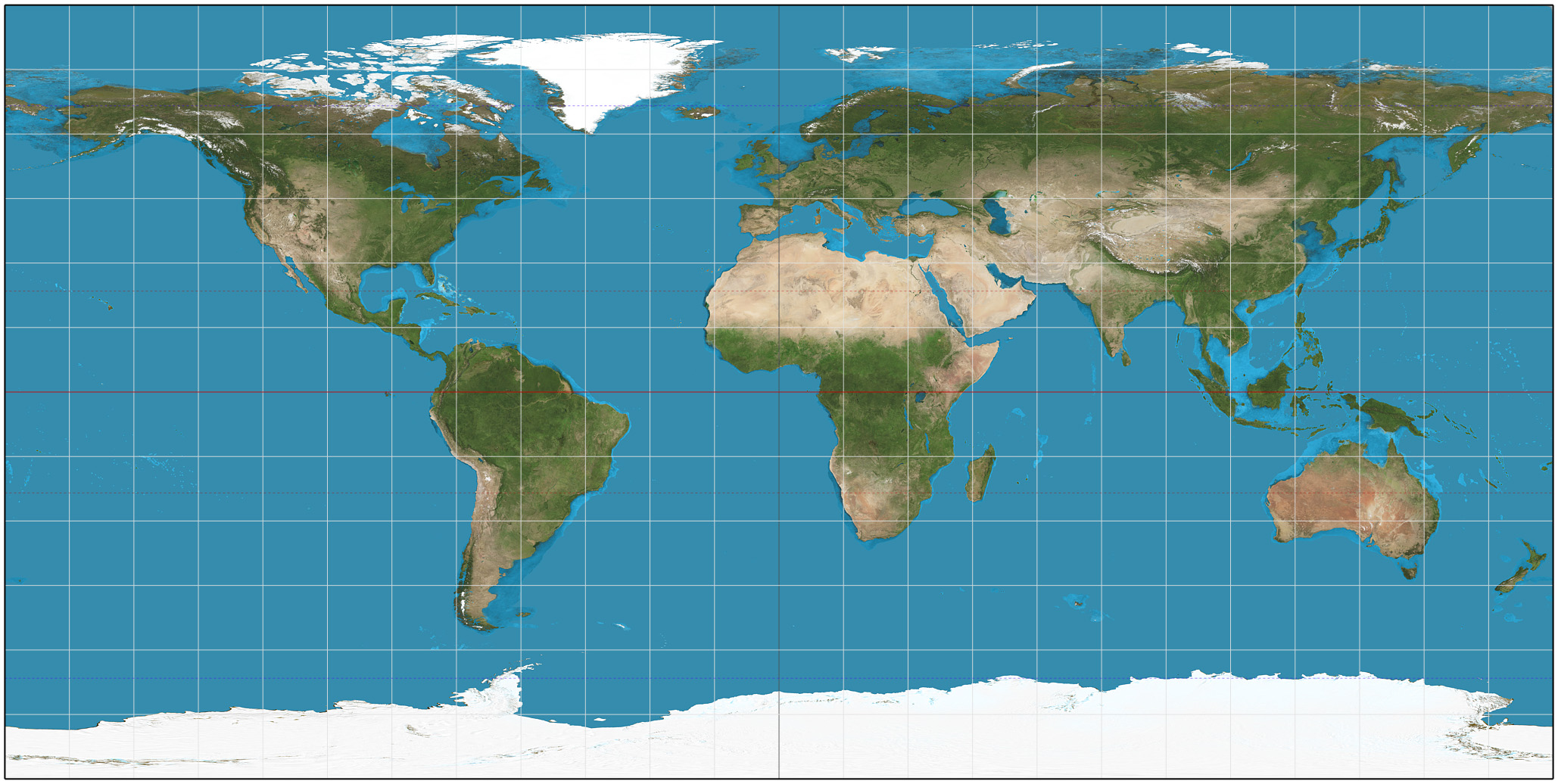
Eckert-Greifendorff Projection
The Eckert-Greifendorff projection is an equal-area map projection described by Max Eckert-Greifendorff in 1935. Unlike his previous six projections, it is not pseudocylindrical. Development Directly inspired by the Hammer projection, Eckert-Greifendorff suggested the use of the equatorial form of the Lambert azimuthal equal-area projection instead of Aitoff's use of the azimuthal equidistant projection: :\begin x &= 2\operatorname_x\left(\frac, \varphi\right) \\ y &= \tfrac12 \operatorname_y\left(\frac, \varphi\right) \end where laea and laea are the ''x'' and ''y'' components of the equatorial Lambert azimuthal equal-area projection. Written out explicitly: :\begin x &= \frac \\ y &= \frac \end The inverse is calculated with the intermediate variable :z \equiv \sqrt The longitude and latitudes can then be calculated by :\begin \lambda &= 4 \arctan \frac \\ \varphi &= \arcsin zy \end where ''λ'' is the longitude from the central meridian and ''φ'' is the latitude.Weisstein ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equal-area Projection
In cartography, an equal-area projection is a map projection that preserves area measure, generally distorting shapes in order to do that. Equal-area maps are also called equivalent or authalic. An equal-area map projection cannot be conformal, nor can a conformal map projection be equal-area. Several equivalent projections were developed in an attempt to minimize the distortion of countries and continents of planet Earth, keeping the area constant. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, etc. Description Equal area representation implies that a region of interest in a particular portion of the map will share the same proportion of area as in any other part of the map. Statistical grid The term "statistical grid" refers to a discrete grid (global or local) of an equal-area surface representation, used for data visualization, geocode and statistical spatial analysi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projection
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Eckert-Greifendorff
Max Eckert (after 1934, Max Eckert-Greifendorff: 10 April 1868 in Chemnitz, Kingdom of Saxony – 26 December 1938, in Aachen) was a German geographer. Biography He received his education in Löbau and Berlin, and taught for some time at Löbau and Leipzig. In 1903, he became Privatdozent at Kiel University. In 1907, he was appointed to the chair of geography in the Royal Technical High School of Aachen (Aix-la-Chapelle). He invented the six Eckert projections and others such as Eckert-Greifendorff projection Writings He has published ''Schulatlas'' (School atlas, 45th ed., 1912), ''Wesen und Aufgabe der Wirtschafts- und Verkehrsgeographie'' (Essentials and purpose of economic and transportation geography, 1903), ''Grundriss der Handelsgeographie'' (Fundamentals of the geography of trade, 1905), ''Leitfaden der Handelsgeographie'' (Primer of the geography of trade, 3d ed., 1911), ''Neue Entwürfe für Erdkarten'' (New ideas for world maps, 1906), ''Die Kartographie als Wissen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckert Projection
The Eckert projections are six pseudocylindrical map projections devised by Max Eckert-Greifendorff, who presented them in 1906. The latitudes are parallel lines in all six projections. The projections come in pairs; in the odd-numbered projections, the latitudes are equally spaced, while their even-numbered counterparts are equal-area. The three pairs are distinguished by the shapes of the meridian Meridian or a meridian line (from Latin ''meridies'' via Old French ''meridiane'', meaning “midday”) may refer to Science * Meridian (astronomy), imaginary circle in a plane perpendicular to the planes of the celestial equator and horizon * ...s. Eckert I and Eckert II have rectilinear (straight-line) meridians, meeting at the equator at an angle. In Eckert III and Eckert IV, meridians are elliptical, while in Eckert V and Eckert VI, they are sinusoidal. {{Map projections Map projections ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hammer Projection
The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide. Development Directly inspired by the Aitoff projection, Hammer suggested the use of the equatorial form of the Lambert azimuthal equal-area projection instead of Aitoff's use of the azimuthal equidistant projection: :\begin x &= \operatorname_x\left(\frac, \varphi\right) \\ y &= \tfrac12 \operatorname_y\left(\frac, \varphi\right) \end where laea and laea are the ''x'' and ''y'' components of the equatorial Lambert azimuthal equal-area projection. Written out explicitly: :\begin x &= \frac \\ y &= \frac \end The inverse is calculated with the intermediate variable :z \equiv \sqrt The longitude and latitudes can then be calculated by :\begin \lambda &= 2 \arctan \frac \\ \varphi &= \arcsin zy \end where ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Azimuthal Equal-area Projection
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection. The Lambert azimuthal projection is used as a map projection in cartography. For example, the National Atlas of the US uses a Lambert azimuthal equal-area projection to display information in the online Map Maker application, and the European Environment Agency recommends its usage for European mapping for statistical analysis and display. It is also used in scientific disciplines such as geology for plotting the orientations of lines in three-dimensional space. This plotting is aided by a special kind of graph paper called a Schmidt net.Ramsay (1967) Definition To defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuthal Equidistant Projection
The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians (lines of longitude) as straight, with distances from the pole represented correctly. The flag of the United Nations contains an example of a polar azimuthal equidistant projection. History While it may have been used by ancient Egyptians for star maps in some holy books,, p.29 the earliest text describing the azimuthal equidistant projection is an 11th-century work by al-Biruni. An example of this system is the world map by ‛Ali b. Ahmad al-Sharafi of Sfax in 1571. The projection appears in many Renaissance maps, and Gerardus Mercator used it for an inset of the north polar regions in sheet 13 and l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitude
Longitude (, ) is a geographic coordinate that specifies the east– west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, England on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west. Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute measure of ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or ''parallels'', run east–west as circles parallel to the equator. Latitude and ''longitude'' are used together as a coordinate pair to specify a location on the surface of the Earth. On its own, the term "latitude" normally refers to the ''geodetic latitude'' as defined below. Briefly, the geodetic latitude of a point is the angle formed between the vector perpendicular (or '' normal'') to the ellipsoidal surface from the point, and the plane of the equator. Background Two levels of abstraction are employed in the definitions of latitude and longitude. In the first step the physical surface is modeled by the geoid, a surface which approximates the mean sea level over the oce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise notable Notability is the property of being worthy of notice, having fame, or being considered to be of a high degree of interest, significance, or distinction. It also refers to the capacity to be such. Persons who are notable due to public responsibi .... Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection ; Cylindrical: In standard presentation, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In standard presentation, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In standard presentation, conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Map Projections
In cartography, map projection is the term used to describe a broad set of transformations employed to represent the two-dimensional curved surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way and to some extent. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, projections are considered in several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |