|
Donald Saari
Donald Gene Saari (born March 1940) is an American mathematician, a Distinguished Professor of Mathematics and Economics and former director of the Institute for Mathematical Behavioral Sciences at the University of California, Irvine. His research interests include the -body problem, the Borda count voting system, and application of mathematics to the social sciences. Contributions Saari has been widely quoted as an expert in voting systems and lottery odds. He is opposed to the use of the Condorcet criterion in evaluating voting systems, and among positional voting schemes he favors using the Borda count over plurality voting, because it reduces the frequency of paradoxical outcomes (which however cannot be avoided entirely in ranking systems because of Arrow's impossibility theorem). For instance, as he has pointed out, plurality voting can lead to situations where the election outcome would remain unchanged if all voters' preferences were reversed; this cannot happen with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Houghton, Michigan
Houghton (; ) is the largest city and county seat of Houghton County, Michigan, Houghton County in the U.S. state of Michigan. Located on the Keweenaw Peninsula, Houghton is the largest city in the Copper Country region. It is the fifth-largest city in the Upper Peninsula of Michigan, Upper Peninsula, with a population of 8,386 at the 2020 United States census. Houghton is the principal city of the Houghton micropolitan area, Michigan, Houghton micropolitan area, which includes all of Houghton and Keweenaw County, Michigan, Keweenaw counties. Houghton lies upon the Keweenaw Waterway, a partly natural, partly artificial waterway connecting at both ends to Lake Superior. Across the waterway from Houghton lies the city of Hancock, Michigan, Hancock. The city of Houghton was named for Douglass Houghton, an American geologist and physician, primarily known for his exploration of the Keweenaw Peninsula. Houghton is home to Michigan Technological University, a public research universi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voting Systems
An electoral or voting system is a set of rules used to determine the results of an election. Electoral systems are used in politics to elect governments, while non-political elections may take place in business, nonprofit organizations and informal organisations. These rules govern all aspects of the voting process: when elections occur, Suffrage, who is allowed to vote, Nomination rules, who can stand as a candidate, Voting method, how ballots are marked and cast, how the ballots are counted, how votes translate into the election outcome, limits on Campaign finance, campaign spending, and other factors that can affect the result. Political electoral systems are defined by constitutions and electoral laws, are typically conducted by election commissions, and can use multiple types of elections for different offices. Some electoral systems elect a single winner to a unique position, such as prime minister, president or governor, while others elect multiple winners, such as membe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to produce ephemeris data. History Modern analytic celestial mechanics started with Isaac Newton's ''Principia'' (1687). The name celestial mechanics is more recent than that. Newton wrote that the field should be called "rational mechanics". The term "dynamics" came in a little later with Gottfried Leibniz, and over a century after Newton, Pierre-Simon Laplace introduced the term ''celestial mechanics''. Prior to Kepler, there was little connection between exact, quantitative prediction of planetary positions, using geometrical or numerical techniques, and contemporary discussions of the physical causes of the planets' motion. Laws of planetary motion Johannes Kepler was the first to closely integrate the predictive geometrical a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
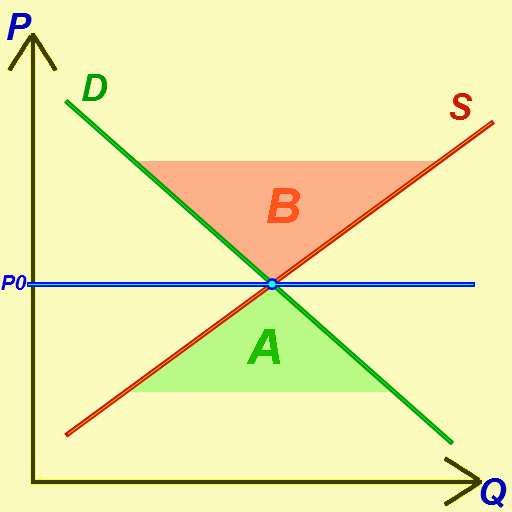
Economic Equilibrium
In economics, economic equilibrium is a situation in which the economic forces of supply and demand are balanced, meaning that economic variables will no longer change. Market equilibrium in this case is a condition where a market price is established through competition such that the amount of goods or services sought by buyers is equal to the amount of goods or services produced by sellers. This price is often called the competitive price or market clearing price and will tend not to change unless demand or supply changes, and quantity is called the "competitive quantity" or market clearing quantity. Understanding economic equilibrium An economic equilibrium is a situation when the economic agent cannot change the situation by adopting any strategy. The concept has been borrowed from the physical sciences. Take a system where physical forces are balanced for instance.This economically interpreted means no further change ensues. Properties of equilibrium Three basic prope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Price Mechanism
In economics, a price mechanism refers to the way in which price determines the allocation of resources and influences the quantity supplied and the quantity demanded of goods and services. The price mechanism, part of a market system, functions in various ways to match up buyers and sellers: as an incentive, a signal, and a rationing system for resources. The price mechanism is an economic model where price plays a key role in directing the activities of producers, consumers, and resource suppliers. An example of a price mechanism uses announced buy and sell prices. Generally speaking, when two parties wish to engage in trade, the purchaser will announce a price he is willing to pay (the Offer and acceptance, offer price) and the seller will announce a price he is willing to accept (the Offer and acceptance, sell price). The primary advantage of such a method is that conditions are laid out in advance, and transactions can proceed with no further permission or authorization fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyses what is viewed as basic elements within economy, economies, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyses economies as systems where production, distribution, consumption, savings, and Expenditure, investment expenditure interact; and the factors of production affecting them, such as: Labour (human activity), labour, Capital (economics), capital, Land (economics), land, and Entrepreneurship, enterprise, inflation, economic growth, and public policies that impact gloss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apportionment (politics)
Apportionment is the process by which seats in a Legislature, legislative body are distributed among administrative divisions, such as states or parties, entitled to Representation (politics), representation. This page presents the general principles and issues related to apportionment. The apportionment by country page describes the specific practices used around the world. The Mathematics of apportionment page describes mathematical formulations and properties of apportionment rules. The simplest and most universal principle is that elections should One man, one vote, give each vote an equal weight. This is both intuitive and stated in laws such as the Fourteenth Amendment to the United States Constitution (the Equal Protection Clause). One example of deliberate malapportionment is seen in bicameral legislatures: while one house, often called a house of commons or representatives, is based on proportional representation, the other is based on regional representation. This is mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tactical Voting
Strategic or tactical voting is voting in consideration of possible ballots cast by other voters in order to maximize one's satisfaction with the election's results. Gibbard's theorem shows that no voting system has a single "always-best" strategy, i.e. one that always maximizes a voter's satisfaction with the result, regardless of other voters' ballots. This implies all voting systems can sometimes encourage voters to strategize. However, weaker guarantees can be shown under stronger conditions. Examples include one-dimensional preferences (where the median rule is strategyproof) and dichotomous preferences (where approval or score voting are strategyproof). With large electoral districts, party list methods tend to be difficult to manipulate in the absence of an electoral threshold. However, biased apportionment methods can create opportunities for strategic voting, as can small electoral districts (e.g. those used most often with the single transferable vote). Proporti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steven Brams
Steven J. Brams (born November 28, 1940) is an American game theorist and political scientist at the New York University Department of Politics. Brams is best known for using the techniques of game theory, public choice theory, and social choice theory to analyze voting systems and fair division. He is one of the independent discoverers of approval voting, as well as extensions of approval voting to multiple-winner elections to give proportional representation of different interests. Brams was a co-discoverer, with Alan Taylor, of the first envy-free cake-cutting solution for ''n'' people. Previous to the Brams-Taylor procedure, the cake-cutting problem had been one of the most important open problems in contemporary mathematics. He is co-inventor with Taylor of the fair-division procedure, adjusted winner, which was patented by New York University in 1999 (# 5,983,205). Brams has applied game theory to a wide variety of strategic situations, from the Bible and theology to int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arrow's Impossibility Theorem
Arrow's impossibility theorem is a key result in social choice theory showing that no ranked-choice procedure for group decision-making can satisfy the requirements of rational choice. Specifically, Arrow showed no such rule can satisfy the independence of irrelevant alternatives axiom. This is the principle that a choice between two alternatives and should not depend on the quality of some third, unrelated option, . The result is often cited in discussions of voting rules, where it shows no ranked voting rule to eliminate the spoiler effect. This result was first shown by the Marquis de Condorcet, whose voting paradox showed the impossibility of logically-consistent majority rule; Arrow's theorem generalizes Condorcet's findings to include non-majoritarian rules like collective leadership or consensus decision-making. While the impossibility theorem shows all ranked voting rules must have spoilers, the frequency of spoilers differs dramatically by rule. Plurality-rule me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plurality Voting
Plurality voting refers to electoral systems in which the candidates in an electoral district who poll more than any other (that is, receive a plurality) are elected. Under single-winner plurality voting, and in systems based on single-member districts, plurality voting is called single member istrictplurality (SMP), which is widely known as " first-past-the-post". In SMP/FPTP the leading candidate, whether or not they have a majority of votes, is elected. There are several versions of plurality voting for multi-member district. The system that elects multiple winners at once with the plurality rule and where each voter casts as many X votes as the number of seats in a multi-seat district is referred to as plurality block voting. A semi-proportional system that elects multiple winners elected at once with the plurality rule and where each voter casts more than one vote but fewer than the number of seats to fill in a multi-seat district is known as limited voting. A semi-prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |