|
Disordered Local Moment Picture
The disordered local moment (DLM) picture is a method, in theoretical Solid-state physics, solid state physics, for describing the electronic structure of a Magnetism, magnetic material at a finite temperature, where a probability distribution of sizes and orientations of atomic magnetic moments must be considered. It was pioneered, among others, by Balázs Győrffy, Julie Staunton, Malcolm Stocks, and co-workers. The underlying assumption of the DLM picture is similar to the Born-Oppenheimer approximation for the separation of solution of the ionic and electronic problems in a material. In the disordered local moment picture, it is assumed that 'local' magnetic moments which form around atoms are sufficiently long-lived that the electronic problem can be solved for an assumed, fixed distribution of magnetic moments. Many such distributions can then be averaged over, appropriately weighted by their probabilities, and a description of the paramagnetic state obtained. (A paramagnetic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent Potential Approximation
The coherent potential approximation (CPA) is a method, in theoretical physics, of finding the averaged Green's function of an inhomogeneous (or disordered) system. The Green's function obtained via the CPA then describes an effective medium whose scattering properties represent the averaged scattering properties of the disordered system being approximated. It is often described as the 'best' single-site theory for obtaining the averaged Green's function. It is perhaps most famous for its use in describing the physical properties of alloys and disordered magnetic systems, although it is also a useful concept in understanding how sound waves scatter in a material which displays spatial inhomogeneity. The coherent potential approximation was first described by Paul Soven, and its application in the context of calculations of the electronic structure of materials was pioneered by Balász Győrffy. Electronic Structure (KKR-CPA) In the context of calculations of the electronic struc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Samarium–cobalt Magnet
Samarium–cobalt (SmCo) magnets belong to the category of rare-earth magnets and are composed of samarium (Sm), a rare-earth element, and cobalt (Co), a transition metal. They are among the strongest permanent magnets. They were developed in the early 1960s based on work done by Karl Strnat at Wright-Patterson Air Force Base and Alden Ray at the University of Dayton. In particular, Strnat and Ray developed the first formulation of SmCo5. Samarium–Cobalt magnets are generally ranked similarly in strength to neodymium magnets, but have higher temperature ratings and higher coercivity. Attributes Some attributes of samarium-cobalts are: * Samarium–cobalt magnets are extremely resistant to demagnetization. * These magnets have good temperature stability maximum use temperatures between and Curie temperatures from to . * They are expensive and subject to price fluctuations (cobalt is market price sensitive). * Samarium–cobalt magnets have a strong resistance to corrosi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permanent Magnets
Permanent may refer to: Art and entertainment * ''Permanent'' (film), a 2017 American film * ''Permanent'' (Joy Division album) * "Permanent" (song), by David Cook *"Permanent", a song by Alex Lahey from '' The Answer Is Always Yes'', 2023 Other uses * Permanent (mathematics), a concept in linear algebra * Permanent (cycling event) * Permanent wave, a hairstyling process See also * Permanence (other) *'' Permanently'', a 2000 album by Mark Wills * Endless (other) * Eternal (other) * Forever (other) * Impermanence, Buddhist concept * {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
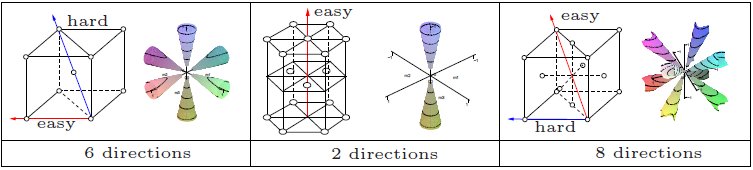
Magnetocrystalline Anisotropy
In physics, a ferromagnetic material is said to have magnetocrystalline anisotropy if it takes more energy to magnetization, magnetize it in certain directions than in others. These directions are usually related to the crystal structure, principal axes of its crystal lattice. It is a special case of magnetic anisotropy. In other words, the excess energy required to magnetize a specimen in a particular direction over that required to magnetize it along the easy direction is called crystalline anisotropy energy. Causes The spin-orbit interaction is the primary source of magnetocrystalline anisotropy. It is basically the orbital motion of the electrons which couples with crystal electric field giving rise to the first order contribution to magnetocrystalline anisotropy. The second order arises due to the mutual interaction of the magnetic dipoles. This effect is weak compared to the exchange interaction and is difficult to compute from first principles, although some successful co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxide
An oxide () is a chemical compound containing at least one oxygen atom and one other element in its chemical formula. "Oxide" itself is the dianion (anion bearing a net charge of −2) of oxygen, an O2− ion with oxygen in the oxidation state of −2. Most of the Earth's crust consists of oxides. Even materials considered pure elements often develop an oxide coating. For example, aluminium foil develops a thin skin of (called a passivation layer) that protects the foil from further oxidation.Greenwood, N. N.; & Earnshaw, A. (1997). Chemistry of the Elements (2nd Edn.), Oxford:Butterworth-Heinemann. . Stoichiometry Oxides are extraordinarily diverse in terms of stoichiometries (the measurable relationship between reactants and chemical equations of an equation or reaction) and in terms of the structures of each stoichiometry. Most elements form oxides of more than one stoichiometry. A well known example is carbon monoxide and carbon dioxide.Greenwood, N. N.; & Earnsh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rare-earth Element
The rare-earth elements (REE), also called the rare-earth metals or rare earths, and sometimes the lanthanides or lanthanoids (although scandium and yttrium, which do not belong to this series, are usually included as rare earths), are a set of 17 nearly indistinguishable lustrous silvery-white soft heavy metals. Compounds containing rare earths have diverse applications in electrical and electronic components, lasers, glass, magnetic materials, and industrial processes. The term "rare-earth" is a misnomer because they are not actually scarce, but historically it took a long time to isolate these elements. They are relatively plentiful in the entire Earth's crust (cerium being the 25th-most-abundant element at 68 parts per million, more abundant than copper), but in practice they are spread thinly as trace impurities, so to obtain rare earths at usable purity requires processing enormous amounts of raw ore at great expense; thus the name "rare" earths. Scandium and yttrium are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transition Metal
In chemistry, a transition metal (or transition element) is a chemical element in the d-block of the periodic table (groups 3 to 12), though the elements of group 12 (and less often group 3) are sometimes excluded. The lanthanide and actinide elements (the f-block) are called inner transition metals and are sometimes considered to be transition metals as well. They are lustrous metals with good electrical and thermal conductivity. Most (with the exception of group 11 and group 12) are hard and strong, and have high melting and boiling temperatures. They form compounds in any of two or more different oxidation states and bind to a variety of ligands to form coordination complexes that are often coloured. They form many useful alloys and are often employed as catalysts in elemental form or in compounds such as coordination complexes and oxides. Most are strongly paramagnetic because of their unpaired d electrons, as are many of their compounds. All of the elements that are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curie Temperature
In physics and materials science, the Curie temperature (''T''C), or Curie point, is the temperature above which certain materials lose their permanent magnetic properties, which can (in most cases) be replaced by induced magnetism. The Curie temperature is named after Pierre Curie, who showed that magnetism is lost at a critical temperature. The force of magnetism is determined by the magnetic moment, a dipole moment within an atom that originates from the angular momentum and spin of electrons. Materials have different structures of intrinsic magnetic moments that depend on temperature; the Curie temperature is the critical point at which a material's intrinsic magnetic moments change direction. Permanent magnetism is caused by the alignment of magnetic moments, and induced magnetism is created when disordered magnetic moments are forced to align in an applied magnetic field. For example, the ordered magnetic moments (ferromagnetic, Figure 1) change and become disordered ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ising Model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent Nuclear magnetic moment, magnetic dipole moments of atomic "spins" that can be in one of two states (+1 or −1). The spins are arranged in a Graph (abstract data type), graph, usually a lattice (group), lattice (where the local structure repeats periodically in all directions), allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases.The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition. Though it is a highly simplified model of a magnetic material, the Ising model can sti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–orbit Interaction
In quantum mechanics, the spin–orbit interaction (also called spin–orbit effect or spin–orbit coupling) is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two effects: the apparent magnetic field seen from the electron perspective due to special relativity and the magnetic moment of the electron associated with its intrinsic spin due to quantum mechanics. For atoms, energy level splitting produced by the spin–orbit interaction is usually of the same order in size as the relativistic corrections to the kinetic energy and the zitterbewegung ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Muffin-tin Approximation
The muffin-tin approximation is a shape approximation of the potential well in a crystal lattice. It is most commonly employed in quantum mechanical simulations of the electronic band structure in solids. The approximation was proposed by John C. Slater. Augmented plane wave method (APW) is a method which uses muffin-tin approximation. It is a method to approximate the energy states of an electron in a crystal lattice. The basic approximation lies in the potential in which the potential is assumed to be spherically symmetric in the muffin-tin region and constant in the interstitial region. Wave functions (the augmented plane waves) are constructed by matching solutions of the Schrödinger equation within each sphere with plane-wave solutions in the interstitial region, and linear combinations of these wave functions are then determined by the variational method. Many modern electronic structure methods employ the approximation. Among them APW method, the linear muffin-tin orbit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |