|
Dirac Semi-metal
In physics, Dirac cones are features that occur in some electronic band structures that describe unusual electron transport properties of materials like graphene and topological insulators. In these materials, at energies near the Fermi level, the Valence and conduction bands, valence band and conduction band take the shape of the upper and lower halves of a conical surface, meeting at what are called Dirac points. Typical examples include graphene, topological insulators, bismuth antimony thin films and some other novel nanomaterials, in which the electronic energy and momentum have a linear dispersion relation such that the electronic band structure near the Fermi level takes the shape of an upper conical surface for the electrons and a lower conical surface for the holes. The two conical surfaces touch each other and form a zero-band gap semimetal. The name of Dirac cone comes from the Dirac equation that can describe relativistic particles in quantum mechanics, proposed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
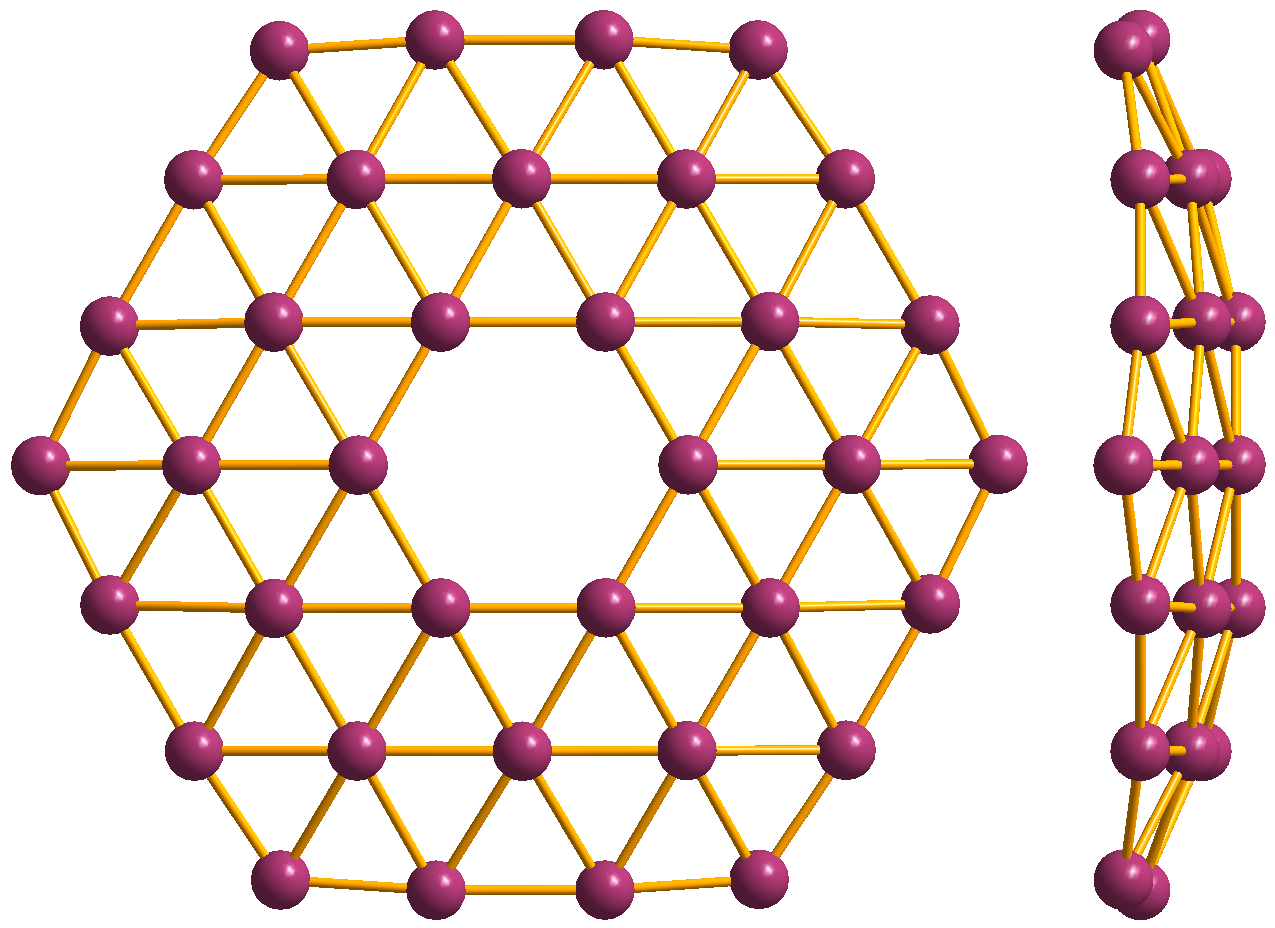
Graphene Brillouin Zone & Linear Dispersion
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating the presence of double bonds within the carbon structure. Graphene is known for its exceptionally high Ultimate tensile strength, tensile strength, Electrical resistivity and conductivity, electrical conductivity, Transparency and translucency, transparency, and being the thinnest two-dimensional material in the world. Despite the nearly transparent nature of a single graphene sheet, graphite (formed from stacked layers of graphene) appears black because it absorbs all visible light wavelengths. On a microscopic scale, graphene is the strongest material ever measured. The existence of graphene was first theorized in 1947 by P. R. Wallace, Philip R. Wallace during his research on graphite's electronic properties, while the term ''graphen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andre Geim
Sir Andre Konstantin Geim (; born 21 October 1958; IPA1 pronunciation: ɑːndreɪ gaɪm) is a Russian-born Dutch–British physicist working in England in the School of Physics and Astronomy at the University of Manchester. Geim was awarded the 2010 Nobel Prize in Physics jointly with Konstantin Novoselov for his work on graphene. He is Regius Professor of Physics and Royal Society Research Professor at the National Graphene Institute. Geim was previously awarded an Ig Nobel Prize in 2000 for levitating a frog using its intrinsic magnetism. He is the first and only individual, as of 2025, to have received both Nobel and Ig Nobel prizes, for which he holds a Guinness World Record. Education Andre Geim was born to Konstantin Alekseyevich Geim and Nina Nikolayevna Bayer in Sochi, Russia, on 21 October 1958. Both his parents were engineers of German origin; Geim says his maternal great-grandmother was Jewish. His grandfather Nikolay N. Bayer (Mykola Baier in Ukrainian) was a notabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypercone
In geometry, a hypercone (or spherical cone) is the figure in the 4-dimensional Euclidean space represented by the equation :x^2 + y^2 + z^2 - w^2 = 0. It is a quadric surface, and is one of the possible 3-manifolds which are 4-dimensional equivalents of the conical surface in 3 dimensions. It is also named "spherical cone" because its intersections with hyperplanes perpendicular to the ''w''-axis are spheres. A four-dimensional right hypercone can be thought of as a sphere which expands with time, starting its expansion from a single point source, such that the center of the expanding sphere remains fixed. An oblique hypercone would be a sphere which expands with time, again starting its expansion from a point source, but such that the center of the expanding sphere moves with a uniform velocity. Parametric form A right spherical hypercone can be described by the function : \vec \sigma (\phi, \theta, t) = (t s \cos \theta \cos \phi, t s \cos \theta \sin \phi, t s \sin \theta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Momentum
In solid-state physics, crystal momentum or quasimomentum is a Momentum#Momentum in quantum mechanics, momentum-like Vector (geometric), vector associated with electrons in a Crystal structure, crystal lattice. It is defined by the associated Reciprocal lattice, wave vectors \mathbf of this lattice, according to \mathbf_ \equiv \hbar \mathbf (where \hbar is the reduced Planck constant). Frequently, crystal momentum is Momentum#Conservation, conserved like mechanical momentum, making it useful to physicists and materials scientists as an analytical tool. Lattice symmetry origins A common method of modeling crystal structure and behavior is to view electrons as Quantum mechanics, quantum mechanical particles traveling through a fixed infinite periodic potential V(x) such that V(\mathbf + \mathbf) = V(\mathbf), where \mathbf is an arbitrary Bravais lattice, lattice vector. Such a model is sensible because crystal Ion, ions that form the lattice structure are typically on the order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface States
Surface states are electronic states found at the Surface (topology), surface of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure from the bulk material to the vacuum. In the weakened potential at the surface, new electronic states can be formed, so called surface states. Origin at condensed matter interfaces As stated by Bloch wave, Bloch's theorem, eigenstates of the single-electron Schrödinger equation with a perfectly periodic potential, a crystal, are Bloch waves : \begin \Psi_ &=\mathrm^u_(\boldsymbol). \end Here u_(\boldsymbol) is a function with the same periodicity as the crystal, ''n'' is the band index and k is the wave number. The allowed wave numbers for a given potential are found by applying the usual Born–von Karman cyclic boundary conditions. The term ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-dimensional Materials
In materials science, the term single-layer materials or 2D materials refers to crystalline solids consisting of a single layer of atoms. These materials are promising for some applications but remain the focus of research. Single-layer materials derived from single elements generally carry the -ene suffix in their names, e.g. graphene. Single-layer materials that are compounds of two or more elements have -ane or -ide suffixes. 2D materials can generally be categorized as either 2D allotropes of various elements or as compounds (consisting of two or more covalently bonding elements). It is predicted that there are hundreds of stable single-layer materials. The atomic structure and calculated basic properties of these and many other potentially synthesisable single-layer materials, can be found in computational databases. 2D materials can be produced using mainly two approaches: top-down exfoliation and bottom-up synthesis. The exfoliation methods include sonication, mechanical, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphite Intercalation Compound
In the area of solid state chemistry, graphite intercalation compounds are a family of materials prepared from graphite. In particular, the sheets of carbon that comprise graphite can be pried apart by the insertion ( intercalation) of ions. The graphite is viewed as a host and the inserted ions as guests. The materials have the formula where ''n'' ≥ 6. The insertion of the guests increases the distance between the carbon sheets. Common guests are reducing agents such as alkali metals. Strong oxidants also intercalate into graphite. Intercalation involves electron transfer into or out of the carbon sheets. So, in some sense, graphite intercalation compounds are salts. Intercalation is often reversible: the inserted ions can be removed and the sheets of carbon collapse to a graphite-like structure. The properties of graphite intercalation compounds differ from those of the parent graphite. Preparation and structure These materials are prepared by treating graphite wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle-resolved Photoemission Spectroscopy
Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoelectric effect, in which an incoming photon of sufficient energy ejects an electron from the surface of a material. By directly measuring the kinetic energy and emission angle distributions of the emitted photoelectrons, the technique can map the electronic band structure and Fermi surfaces. ARPES is best suited for the study of one- or two-dimensional materials. It has been used by physicists to investigate high-temperature superconductors, graphene, topological materials, quantum well states, and materials exhibiting charge density waves. ARPES systems consist of a monochromatic light source to deliver a narrow beam of photons, a sample holder connected to a manipulator used to position the sample of a material, and an electron spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carrier Mobility
In solid-state physics, the electron mobility characterizes how quickly an electron can move through a metal or semiconductor when pushed or pulled by an electric field. There is an analogous quantity for holes, called hole mobility. The term carrier mobility refers in general to both electron and hole mobility. Electron and hole mobility are special cases of electrical mobility of charged particles in a fluid under an applied electric field. When an electric field ''E'' is applied across a piece of material, the electrons respond by moving with an average velocity called the drift velocity, v_d. Then the electron mobility ''μ'' is defined as v_d = \mu E. Electron mobility is almost always specified in units of cm2/( V⋅ s). This is different from the SI unit of mobility, m2/( V⋅ s). They are related by 1 m2/(V⋅s) = 104 cm2/(V⋅s). Conductivity is proportional to the product of mobility and carrier concentration. For example, the same conductivity could come fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Hall Effect
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhibits steps that take on the quantized values : R_ = \frac = \frac , where is the Hall voltage, is the channel current, is the elementary charge and is the Planck constant. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively. The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation corre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles include all quarks and leptons and all composite particles made of an even and odd, odd number of these, such as all baryons and many atoms and atomic nucleus, nuclei. Fermions differ from bosons, which obey Bose–Einstein statistics. Some fermions are elementary particles (such as electrons), and some are composite particles (such as protons). For example, according to the spin-statistics theorem in Theory of relativity, relativistic quantum field theory, particles with integer Spin (physics), spin are bosons. In contrast, particles with half-integer spin are fermions. In addition to the spin characteristic, fermions have another specific property: they possess conserved baryon or lepton quantum numbers. Therefore, what is usually referr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charge Carriers
In solid state physics, a charge carrier is a particle or quasiparticle that is free to move, carrying an electric charge, especially the particles that carry electric charges in electrical conductors. Examples are electrons, ions and holes. In a conducting medium, an electric field can exert force on these free particles, causing a net motion of the particles through the medium; this is what constitutes an electric current. The electron and the proton are the elementary charge carriers, each carrying one elementary charge (''e''), of the same magnitude and opposite sign. In conductors In conducting mediums, particles serve to carry charge. In many metals, the charge carriers are electrons. One or two of the valence electrons from each atom are able to move about freely within the crystal structure of the metal. The free electrons are referred to as conduction electrons, and the cloud of free electrons is called a Fermi gas. Many metals have electron and hole bands. In som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |