|
Differential Dynamic Programming
Differential dynamic programming (DDP) is an optimal control algorithm of the trajectory optimization class. The algorithm was introduced in 1966 by David Mayne, Mayne and subsequently analysed in Jacobson and Mayne's eponymous book. The algorithm uses locally-quadratic models of the dynamics and cost functions, and displays Rate of convergence, quadratic convergence. It is closely related to Pantoja's step-wise Newton's method. Finite-horizon discrete-time problems The dynamics describe the evolution of the state \textstyle\mathbf given the control \mathbf from time i to time i+1. The ''total cost'' J_0 is the sum of running costs \textstyle\ell and final cost \ell_f, incurred when starting from state \mathbf and applying the control sequence \mathbf \equiv \ until the horizon is reached: :J_0(\mathbf,\mathbf)=\sum_^\ell(\mathbf_i,\mathbf_i) + \ell_f(\mathbf_N), where \mathbf_0\equiv\mathbf, and the \mathbf_i for i>0 are given by . The solution of the optimal control probl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Control
Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory. Optimal control is an extension of the calculus of variations, and is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and Richard Bellman in the 1950s, after contributions to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trajectory Optimization
Trajectory optimization is the process of designing a trajectory that minimizes (or maximizes) some measure of performance while satisfying a set of constraints. Generally speaking, trajectory optimization is a technique for computing an open-loop solution to an optimal control problem. It is often used for systems where computing the full closed-loop solution is not required, impractical or impossible. If a trajectory optimization problem can be solved at a rate given by the inverse of the Lipschitz constant, then it can be used iteratively to generate a closed-loop solution in the sense of Caratheodory. If only the first step of the trajectory is executed for an infinite-horizon problem, then this is known as Model Predictive Control (MPC). Although the idea of trajectory optimization has been around for hundreds of years (calculus of variations, brachystochrone problem), it only became practical for real-world problems with the advent of the computer. Many of the original ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Mayne
David Quinn Mayne, FRS, FIEEE, FREng (born 23 April 1930) is a British academic, engineer, teacher and author. Career Mayne began his career in 1950 as a lecturer at the University of the Witwatersrand (1950–54; 1957–59). He lectured at Imperial College London from 1959-67 and also received his PhD in 1967 at the University of London under John Westcott. He was a Research Fellow at Harvard (1971). At Imperial College he was professor of control theory (1971–91) as well as concurrently heading the Department of Electrical Engineering (1984–88). He was a professor in the Dept. of Electrical and Computer Engineering at University of California, Davis from 1989-96. From 1996 he has been a professor emeritus. He was named honorary professor at Beihang University in Beijing in 2006. His students include Peter Caines. Awards and affiliations * Giorgio Quazza Medal, 2014 * IEEE Control Systems Award, 2009 * Hon. DTech Lund University, 1995 * Hon, Fellow Imperial College ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Of Convergence
In numerical analysis, the order of convergence and the rate of convergence of a convergent sequence are quantities that represent how quickly the sequence approaches its limit. A sequence (x_n) that converges to x^* is said to have ''order of convergence'' q \geq 1 and ''rate of convergence'' \mu if : \lim _ \frac=\mu. The rate of convergence \mu is also called the ''asymptotic error constant''. Note that this terminology is not standardized and some authors will use ''rate'' where this article uses ''order'' (e.g., ). In practice, the rate and order of convergence provide useful insights when using iterative methods for calculating numerical approximations. If the order of convergence is higher, then typically fewer iterations are necessary to yield a useful approximation. Strictly speaking, however, the asymptotic behavior of a sequence does not give conclusive information about any finite part of the sequence. Similar concepts are used for discretization methods. The solutio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Programming
Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics. In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have '' optimal substructure''. If sub-problems can be nested recursively inside larger problems, so that dynamic programming methods are applicable, then there is a relation between the value of the larger problem and the values of the sub-problems.Cormen, T. H.; Leiserson, C. E.; Riv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
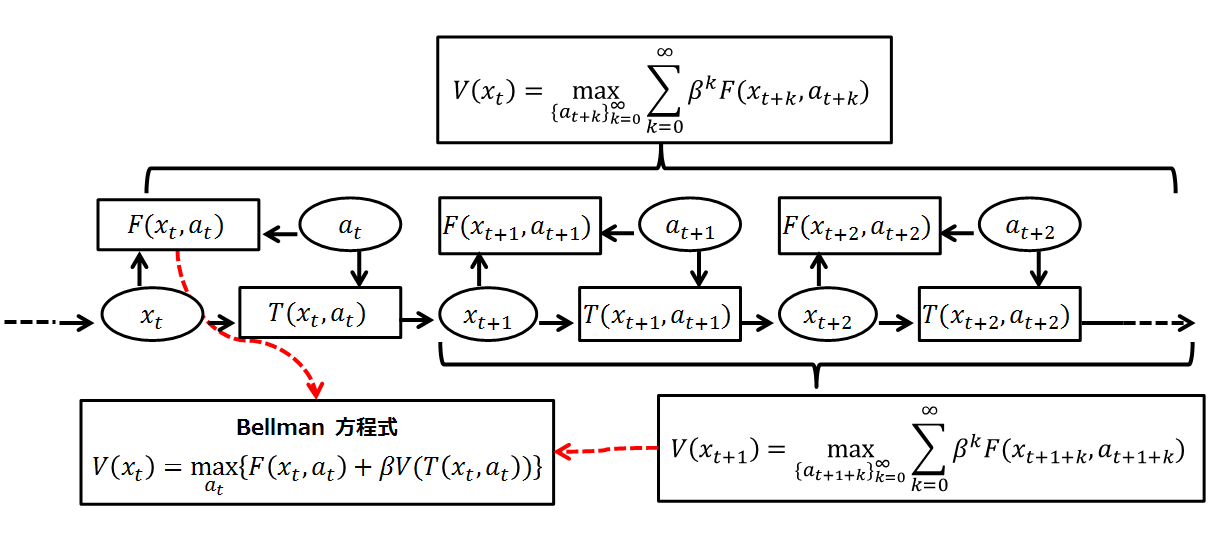
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ''Theory of Games and Econ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Method
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function. The most basic version starts with a single-variable function defined for a real variable , the function's derivative , and an initial guess for a root of . If the function satisfies sufficient assumptions and the initial guess is close, then :x_ = x_0 - \frac is a better approximation of the root than . Geometrically, is the intersection of the -axis and the tangent of the graph of at : that is, the improved guess is the unique root of the linear approximation at the initial point. The process is repeated as :x_ = x_n - \frac until a sufficiently precise value is reached. This algorithm is first in the class of Householder's methods, succeeded by Halley's method. The method can also be extended to complex fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line-search
In optimization, the line search strategy is one of two basic iterative approaches to find a local minimum \mathbf^* of an objective function f:\mathbb R^n\to\mathbb R. The other approach is trust region. The line search approach first finds a descent direction along which the objective function f will be reduced and then computes a step size that determines how far \mathbf should move along that direction. The descent direction can be computed by various methods, such as gradient descent or quasi-Newton method. The step size can be determined either exactly or inexactly. Example use Here is an example gradient method that uses a line search in step 4. # Set iteration counter \displaystyle k=0, and make an initial guess \mathbf_0 for the minimum # Repeat: # Compute a descent direction \mathbf_k # Choose \displaystyle \alpha_k to 'loosely' minimize h(\alpha_k)=f(\mathbf_k+\alpha_k\mathbf_k) over \alpha_k\in\mathbb R_+ # ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z^* Mz is positive for every nonzero complex column vector z, where z^* denotes the conjugate transpose of z. Positive semi-definite matrices are defined similarly, except that the scalars z^\textsfMz and z^* Mz are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called indefinite. A matrix is thus positive-definite if and only if it is the matrix of a positive-definite quadratic form or Hermitian form. In other words, a matrix is positive-definite if and only if it def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Distribution
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution Translated by J.B. Sykes and M.J. Kearsley. See section 28) is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. The distribution is expressed in the form: :p_i \propto e^ where is the probability of the system being in state , is the energy of that state, and a constant of the distribution is the product of the Boltzmann constant and thermodynamic temperature . The symbol \propto denotes proportionality (see for the proportionality constant). The term ''system'' here has a very wide meaning; it can range from a collection of 'sufficient number' of atoms or a single atom to a macroscopic system such as a natural gas storage tank. Therefore the Boltzmann distribution can be used to solve a very wide variety of problems. The distrib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |