|
Differential Algebraic Equation
In mathematics, a differential-algebraic system of equations (DAE) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system. The set of the solutions of such a system is a ''differential algebraic variety'', and corresponds to an ideal in a differential algebra of differential polynomials. In the univariate case, a DAE in the variable ''t'' can be written as a single equation of the form :F(\dot x, x, t)=0, where x(t) is a vector of unknown functions and the overdot denotes the time derivative, i.e., \dot x = \frac. They are distinct from ordinary differential equation (ODE) in that a DAE is not completely solvable for the derivatives of all components of the function ''x'' because these may not all appear (i.e. some equations are algebraic); technically the distinction between an implicit ODE system hat may be rendered explicitand a DAE system is that the Jacobian matrix \frac is a singular matrix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Nodal Analysis
In electrical engineering, modified nodal analysis or MNA is an extension of nodal analysis which not only determines the circuit's node voltages (as in classical nodal analysis), but also ''some'' branch currents. Modified nodal analysis was developed as a formalism to mitigate the difficulty of representing voltage-defined components in nodal analysis (e.g. voltage-controlled voltage sources). It is one such formalism. Others, such as sparse tableau formulation, are equally general and related via matrix transformations. Method The MNA uses the element's ''branch constitutive equations'' or BCE, i.e., their voltage - Electric current, current characteristic and the Kirchhoff's circuit laws. The method is often done in four steps, but it can be reduced to three: Step 1 Write the Kirchhoff's current law, KCL equations of the circuit. At each node of an electric circuit, write the currents coming into and out of the node. Take care, however, in the MNA method, the current of the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
APMonitor
Advanced process monitor (APMonitor) is a modeling language for differential algebraic ( DAE) equations. It is a free web-service or local server for solving representations of physical systems in the form of implicit DAE models. APMonitor is suited for large-scale problems and solves linear programming, integer programming, nonlinear programming, nonlinear mixed integer programming, dynamic simulation, moving horizon estimation, and nonlinear model predictive control. APMonitor does not solve the problems directly, but calls nonlinear programming solvers such as APOPT, BPOPT, IPOPT, MINOS, and SNOPT. The APMonitor API provides exact first and second derivatives of continuous functions to the solvers through automatic differentiation and in sparse matrix form. Programming language integration Julia, MATLAB, Python are mathematical programming languages that have APMonitor integration through web-service APIs. The GEKKO Optimization Suite is a recent extension of APMonitor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Derivative Index Reduction Method
Dummy may refer to: Dolls * Mannequin, a model of the human body * Dummy (ventriloquism) * Crash test dummy People * Dummy (nickname), several people with the nickname * Dummy, the Witch of Sible Hedingham (c. 1788–1863), one of the last people to be accused of being a witch in England Arts and entertainment Characters * Dummy (Marvel Comics), from the comic book ''X-Men'' * Dummy (DC Comics) Films * ''Dummy'' (1979 film), a TV movie starring LeVar Burton and Paul Sorvino * ''Dummy'' (2002 film), a comedy/drama * ''Dummy'', a 2009 coming-of-age drama starring Emma Catherwood * ''Dummy'', a short film by Kira Muratova * ''The Dummy'' (1917 film), an American silent drama * ''The Dummy'' (1929 film), an American comedy Music * Dummy (band), a band from Los Angeles * ''Dummy'' (album), 1994, by Portishead * "Dummy", a song by 6ix9ine from the album ''Dummy Boy'' * "Dummy!", a track from the soundtrack of the 2015 video game ''Undertale by Toby Fox'' * "Dummy", a song by P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pantelides Algorithm
Pantelides algorithm in mathematics is a systematic method for reducing high-index systems of differential-algebraic equations to lower index. This is accomplished by selectively adding differentiated forms of the equations already present in the system. It is possible for the algorithm to fail in some instances. Pantelides algorithm is implemented in several significant equation-based simulation programs such as gPROMS, Modelica Modelica is an object-oriented, declarative, multi-domain modeling language for component-oriented modeling of complex systems, e.g., systems containing mechanical, electrical, electronic, hydraulic, thermal, control, electric power or process ... and EMSO. a free-to-use closed-source simulator/equation solver that includes implementation for the Pantelides algorithm. References [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Equations
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For example, x^5-3x+1=0 is an algebraic equation with integer coefficients and :y^4 + \frac - \frac + xy^2 + y^2 + \frac = 0 is a multivariate polynomial equation over the rationals. For many authors, the term ''algebraic equation'' refers only to the univariate case, that is polynomial equations that involve only one variable. On the other hand, a polynomial equation may involve several variables (the ''multivariate'' case), in which case the term ''polynomial equation'' is usually preferred. Some but not all polynomial equations with rational coefficients have a solution that is an algebraic expression that can be found using a finite number of operations that involve only those same types of coefficients (that is, can be solved algebraically). This can be done for all such equati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equations
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with any other DE, its unknown(s) consists of one (or more) function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with ''partial'' differential equations (PDEs) which may be with respect to one independent variable, and, less commonly, in contrast with ''stochastic'' differential equations (SDEs) where the progression is random. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where a_0(x),\ldots,a_n(x) and b(x) are arbitrary differentiable functions that do not need to be linear, and y',\ldots, y^ are the successive derivatives of the unknown function y of the variable x. Among ord ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Function Theorem
In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does so by representing the relation as the graph of a function. There may not be a single function whose graph can represent the entire relation, but there may be such a function on a restriction of the domain of the relation. The implicit function theorem gives a sufficient condition to ensure that there is such a function. More precisely, given a system of equations (often abbreviated into ), the theorem states that, under a mild condition on the partial derivatives (with respect to each ) at a point, the variables are differentiable functions of the in some neighborhood of the point. As these functions generally cannot be expressed in closed form, they are ''implicitly'' defined by the equations, and this motivated the name of the theorem. In other words, under a mild condition on the partial derivatives, the set of zero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
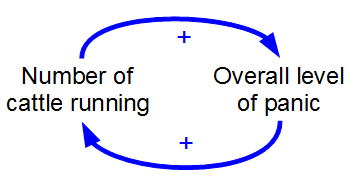
Positive Feedback
Positive feedback (exacerbating feedback, self-reinforcing feedback) is a process that occurs in a feedback loop where the outcome of a process reinforces the inciting process to build momentum. As such, these forces can exacerbate the effects of a small disturbance. That is, the effects of a perturbation on a system include an increase in the magnitude of the perturbation. That is, ''A produces more of B which in turn produces more of A''.Keesing, R.M. (1981). Cultural anthropology: A contemporary perspective (2nd ed.) p.149. Sydney: Holt, Rinehard & Winston, Inc. In contrast, a system in which the results of a change act to reduce or counteract it has negative feedback. Both concepts play an important role in science and engineering, including biology, chemistry, and cybernetics. Mathematically, positive feedback is defined as a positive loop gain around a closed loop of cause and effect. That is, positive feedback is Phase (waves), in phase with the input, in the sense that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operational Amplifiers
An operational amplifier (often op amp or opamp) is a DC-coupled electronic voltage amplifier with a differential input, a (usually) single-ended output, and an extremely high gain. Its name comes from its original use of performing mathematical operations in analog computers. By using negative feedback, an op amp circuit's characteristics (e.g. its gain, input and output impedance, bandwidth, and functionality) can be determined by external components and have little dependence on temperature coefficients or engineering tolerance in the op amp itself. This flexibility has made the op amp a popular building block in analog circuits. Today, op amps are used widely in consumer, industrial, and scientific electronics. Many standard integrated circuit op amps cost only a few cents; however, some integrated or hybrid operational amplifiers with special performance specifications may cost over . Op amps may be packaged as components or used as elements of more complex integrat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Netlist
In electronic design, a netlist is a description of the connectivity of an electronic circuit. In its simplest form, a netlist consists of a list of the electronic components in a circuit and a list of the nodes they are connected to. A network (net) is a collection of two or more interconnected components. The structure, complexity and representation of netlists can vary considerably, but the fundamental purpose of every netlist is to convey connectivity information. Netlists usually provide nothing more than instances, nodes, and perhaps some attributes of the components involved. If they express much more than this, they are usually considered to be a hardware description language such as Verilog or VHDL, or one of several languages specifically designed for input to simulators or hardware compilers (such as SPICE analog simulation netlists). Types of netlists Netlists can be: * Physical (based upon physical connections) or logical (based upon logical connections) ** ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematica
Wolfram (previously known as Mathematica and Wolfram Mathematica) is a software system with built-in libraries for several areas of technical computing that allows machine learning, statistics, symbolic computation, data manipulation, network analysis, time series analysis, NLP, optimization, plotting functions and various types of data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other programming languages. It was conceived by Stephen Wolfram, and is developed by Wolfram Research of Champaign, Illinois. The Wolfram Language is the programming language used in ''Mathematica''. Mathematica 1.0 was released on June 23, 1988 in Champaign, Illinois and Santa Clara, California. Mathematica's Wolfram Language is fundamentally based on Lisp; for example, the Mathematica command Most is identically equal to the Lisp command butlast. There is a substantial literature on the development of computer algebra systems (CAS). __TOC_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |