|
Deontic Modal Logic
Deontic logic is the field of philosophical logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. It can be used to formalize imperative logic, or directive modality in natural languages. Typically, a deontic logic uses ''OA'' to mean ''it is obligatory that A'' (or ''it ought to be (the case) that A''), and ''PA'' to mean ''it is permitted (or permissible) that A'', which is defined as PA\equiv \neg O\neg A. In natural language, the statement "You may go to the zoo OR the park" should be understood as Pz\land Pp instead of Pz\lor Pp, as both options are permitted by the statement. When there are multiple agents involved in the domain of discourse, the deontic modal operator can be specified to each agent to express their individual obligations and permissions. For example, by using a subscript O_i for agent a_i, O_iA means that "It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophical Logic
Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophical logic in a wider sense as the study of the scope and nature of logic in general. In this sense, philosophical logic can be seen as identical to the philosophy of logic, which includes additional topics like how to define logic or a discussion of the fundamental concepts of logic. The current article treats philosophical logic in the narrow sense, in which it forms one field of inquiry within the philosophy of logic. An important issue for philosophical logic is the question of how to classify the great variety of non-classical logical systems, many of which are of rather recent origin. One form of classification often found in the literature is to distinguish between extended logics and deviant logics. Logic itself can be defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
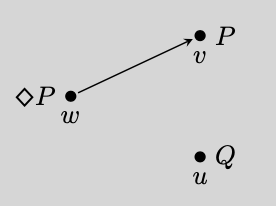
Accessibility Relation
An accessibility relation is a relation (math), relation which plays a key role in assigning truth values to sentences in the Kripke semantics, relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what is true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language linguistic modality, modal statements depend on some, but not all, alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it is raining. Rather, its truth depends on whether such a scenario is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propositional Calculus
The propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. Sometimes, it is called ''first-order'' propositional logic to contrast it with System F, but it should not be confused with first-order logic. It deals with propositions (which can be Truth value, true or false) and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives representing the truth functions of Logical conjunction, conjunction, Logical disjunction, disjunction, Material conditional, implication, Logical biconditional, biconditional, and negation. Some sources include other connectives, as in the table below. Unlike first-order logic, propositional logic does not deal with non-logical objects, predicates about them, or Quantifier (logic), quantifiers. However, all the machinery of pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexius Meinong
Alexius Meinong von Handschuchsheim (; 17 July 1853 – 27 November 1920) was an Austrian philosopher, a realist known for his unique ontology and theory of objects. He also made contributions to philosophy of mind and theory of value. Life Alexius Meinong's father was officer Anton von Meinong (1799–1870), who was granted the hereditary title of Ritter in 1851 and reached the rank of Major General in 1858 before retiring in 1859. From 1868 to 1870, Meinong studied at the Akademisches Gymnasium, Vienna. In 1870, he entered the University of Vienna law school where he was drawn to Carl Menger's lectures on economics. In summer 1874, he earned a doctorate in history by writing a thesis on Arnold of Brescia. It was during the winter term (1874–1875) that he began to focus on history and philosophy. Meinong became a pupil of Franz Brentano, who was then a recent addition to the philosophical faculty. Meinong would later claim that his mentor did not directly influence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernst Mally
Ernst Mally (; ; 11 October 1879 – 8 March 1944) was an Austrian analytic philosopher, initially affiliated with Alexius Meinong's Graz School of object theory. Mally was one of the founders of deontic logic and is mainly known for his contributions in that field of research. In metaphysics, he is known for introducing a distinction between two kinds of predication, better known as the dual predication approach. Life Mally was born in the town of Kranj () in the Duchy of Carniola, Austria-Hungary (now in Slovenia). His father was of Slovene origin, but identified himself with Austrian German culture (he also Germanized the orthography of his surname, originally spelled Mali, a common Slovene surname of Upper Carniola). After his death, the family moved to the Carniolan capital of Ljubljana (). There, Ernst attended the prestigious Ljubljana German-language Gymnasium. Already at a young age, Mally became a fervent supporter of the Pan-German nationalist movement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Sir Isaac Newton, with the creation of calculus in addition to many other branches of mathematics, such as binary arithmetic and statistics. Leibniz has been called the "last universal genius" due to his vast expertise across fields, which became a rarity after his lifetime with the coming of the Industrial Revolution and the spread of specialized labor. He is a prominent figure in both the history of philosophy and the history of mathematics. He wrote works on philosophy, theology, ethics, politics, law, history, philology, games, music, and other studies. Leibniz also made major contributions to physics and technology, and anticipated notions that surfaced much later in probability theory, biology, medicine, geology, psychology, linguistics and computer science. Leibniz contributed to the field ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alethic Logic
Modal logic is a kind of logic used to represent statements about necessity and possibility. In philosophy and related fields it is used as a tool for understanding concepts such as knowledge, obligation, and causation. For instance, in epistemic modal logic, the formula \Box P can be used to represent the statement that P is known. In deontic modal logic, that same formula can represent that P is a moral obligation. Modal logic considers the inferences that modal statements give rise to. For instance, most epistemic modal logics treat the formula \Box P \rightarrow P as a tautology, representing the principle that only true statements can count as knowledge. However, this formula is not a tautology in deontic modal logic, since what ought to be true can be false. Modal logics are formal systems that include unary operators such as \Diamond and \Box, representing possibility and necessity respectively. For instance the modal formula \Diamond P can be read as "possibly P" while ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medieval Philosophy
Medieval philosophy is the philosophy that existed through the Middle Ages, the period roughly extending from the fall of the Western Roman Empire in the 5th century until after the Renaissance in the 13th and 14th centuries. Medieval philosophy, understood as a project of independent philosophical inquiry, began in Baghdad, in the middle of the 8th century, and in France and Germany, in the itinerant court of Charlemagne in Aachen, in the last quarter of the 8th century. It is defined partly by the process of rediscovering the ancient culture developed in Greece and Rome during the Classical period, and partly by the need to address theological problems and to integrate sacred doctrine with secular learning. This is one of the defining characteristics in this time period. Understanding God was the focal point of study of the Jewish, Christian and Muslim Philosophers and Theologians. The history of medieval philosophy is traditionally divided into two main periods: the period ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancient Greece
Ancient Greece () was a northeastern Mediterranean civilization, existing from the Greek Dark Ages of the 12th–9th centuries BC to the end of classical antiquity (), that comprised a loose collection of culturally and linguistically related city-states and communities. Prior to the Roman period, most of these regions were officially unified only once under the Kingdom of Macedon from 338 to 323 BC. In Western history, the era of classical antiquity was immediately followed by the Early Middle Ages and the Byzantine period. Three centuries after the decline of Mycenaean Greece during the Bronze Age collapse, Greek urban poleis began to form in the 8th century BC, ushering in the Archaic period and the colonization of the Mediterranean Basin. This was followed by the age of Classical Greece, from the Greco-Persian Wars to the death of Alexander the Great in 323 BC, and which included the Golden Age of Athens and the Peloponnesian War. The u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Logic (modal Logic)
In logic, philosophy, and theoretical computer science, dynamic logic is an extension of modal logic capable of encoding properties of computer programs. A simple example of a statement in dynamic logic is :\text \to text\text, which states that if the ground is currently dry and it rains, then afterwards the ground will be wet. The syntax of dynamic logic contains a language of ''propositions'' (like "the ground is dry") and a language of ''actions'' (like "it rains"). The core modal constructs are , which states that after performing action ''a'' the proposition ''p'' should hold, and \langle a \rangle p, which states that after performing action ''a'' it is possible that ''p'' holds. The action language supports operations a\mathbinb (doing one action followed by another), a \cup b (doing one action or another), and iteration a (doing one action zero or more times). The proposition language supports Boolean operations (and, or, and not). The action logic is expressive enough ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraconsistent Logic
Paraconsistent logic is a type of non-classical logic that allows for the coexistence of contradictory statements without leading to a logical explosion where anything can be proven true. Specifically, paraconsistent logic is the subfield of logic that is concerned with studying and developing "inconsistency-tolerant" systems of logic, purposefully excluding the principle of explosion. Inconsistency-tolerant logics have been discussed since at least 1910 (and arguably much earlier, for example in the writings of Aristotle); however, the term ''paraconsistent'' ("beside the consistent") was first coined in 1976, by the Peruvian philosopher Francisco Miró Quesada Cantuarias. The study of paraconsistent logic has been dubbed paraconsistency, which encompasses the school of dialetheism. Definition In classical logic (as well as intuitionistic logic and most other logics), contradictions entail everything. This feature, known as the principle of explosion or ''ex contradiction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |