|
Density Matrix Renormalization Group
The density matrix renormalization group (DMRG) is a numerical variational technique devised to obtain the low-energy physics of quantum many-body systems with high accuracy. As a variational method, DMRG is an efficient algorithm that attempts to find the lowest-energy matrix product state wavefunction of a Hamiltonian. It was invented in 1992 by Steven R. White and it is nowadays the most efficient method for 1-dimensional systems. History The first application of the DMRG, by Steven R. White and Reinhard Noack, was a ''toy model'': to find the spectrum of a spin 0 particle in a 1D box. This model had been proposed by Kenneth G. Wilson as a test for any new renormalization group method, because they all happened to fail with this simple problem. The DMRG overcame the problems of previous renormalization group methods by connecting two blocks with the two sites in the middle rather than just adding a single site to a block at each step as well as by using the density matr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Method (quantum Mechanics)
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states. This allows calculating approximate wavefunctions such as molecular orbitals. The basis for this method is the variational principle. The method consists of choosing a "trial wavefunction" depending on one or more parameters, and finding the values of these parameters for which the expectation value of the energy is the lowest possible. The wavefunction obtained by fixing the parameters to such values is then an approximation to the ground state wavefunction, and the expectation value of the energy in that state is an upper bound to the ground state energy. The Hartree–Fock method, density matrix renormalization group, and Ritz method apply the variational method. Description Suppose we are given a Hilbert space and a Hermitian operator over it called the Hamiltonian H . Ignoring complications about continuous spectr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Physics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science, information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. While classical thermodynamics is primarily concerned with thermodynamic equilibrium, statistical mechanics has been applied in non-equilibrium stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dendrimers
Dendrimers are highly ordered, branched polymeric molecules. Synonymous terms for dendrimer include arborols and cascade molecules. Typically, dendrimers are symmetric about the core, and often adopt a spherical three-dimensional morphology. The word dendron is also encountered frequently. A dendron usually contains a single chemically addressable group called the focal point or core. The difference between dendrons and dendrimers is illustrated in the top figure, but the terms are typically encountered interchangeably. The first dendrimers were made by divergent synthesis approaches by Fritz Vögtle in 1978, R.G. Denkewalter at Allied Corporation in 1981, Donald Tomalia at Dow Chemical in 1983 and in 1985, and by George R. Newkome in 1985. In 1990 a convergent synthetic approach was introduced by Craig Hawker and Jean Fréchet. Dendrimer popularity then greatly increased, resulting in more than 5,000 scientific papers and patents by the year 2005. Properties Dendriti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tree Graph
In graph theory, a tree is an undirected graph in which any two vertices are connected by path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees. A directed tree, oriented tree,See .See . polytree,See . or singly connected networkSee . is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. The various kinds of data structures referred to as trees in computer science have underlying graphs that are trees in graph theory, although such data structures are generally rooted trees. A rooted tree may be directed, called a directed rooted tree, either making all its edges point away from the root—in which case it is called an arborescence or out-tree—or ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Wire
In mesoscopic physics, a quantum wire is an electrically conducting wire in which quantum effects influence the transport properties. Usually such effects appear in the dimension of nanometers, so they are also referred to as nanowires. Quantum effects If the diameter of a wire is sufficiently small, electrons will experience quantum confinement in the transverse direction. As a result, their transverse energy will be limited to a series of discrete values. One consequence of this quantization is that the classical formula for calculating the electrical resistance of a wire, : R = \rho \frac, is not valid for quantum wires (where \rho is the material's resistivity, l is the length, and A is the cross-sectional area of the wire). Instead, an exact calculation of the transverse energies of the confined electrons has to be performed to calculate a wire's resistance. Following from the quantization of electron energy, the electrical conductance (the inverse of the resistance) is fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Dots
Quantum dots (QDs) or semiconductor nanocrystals are semiconductor particles a few nanometres in size with optical and electronic properties that differ from those of larger particles via quantum mechanical effects. They are a central topic in nanotechnology and materials science. When a quantum dot is illuminated by UV light, an electron in the quantum dot can be excited to a state of higher energy. In the case of a semiconducting quantum dot, this process corresponds to the transition of an electron from the valence band to the conduction band. The excited electron can drop back into the valence band releasing its energy as light. This light emission ( photoluminescence) is illustrated in the figure on the right. The color of that light depends on the energy difference between the discrete energy levels of the quantum dot in the conduction band and the valence band. In other words, a quantum dot can be defined as a structure on a semiconductor which is capable of confi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boson
In particle physics, a boson ( ) is a subatomic particle whose spin quantum number has an integer value (0, 1, 2, ...). Bosons form one of the two fundamental classes of subatomic particle, the other being fermions, which have half odd-integer spin (1/2, 3/2, 5/2, ...). Every observed subatomic particle is either a boson or a fermion. Paul Dirac coined the name ''boson'' to commemorate the contribution of Satyendra Nath Bose, an Indian physicist. Some bosons are elementary particles occupying a special role in particle physics, distinct from the role of fermions (which are sometimes described as the constituents of "ordinary matter"). Certain elementary bosons (e.g. gluons) act as force carriers, which give rise to forces between other particles, while one (the Higgs boson) contributes to the phenomenon of mass. Other bosons, such as mesons, are composite particles made up of smaller constituents. Outside the realm of particle physics, multiple identical composite bosons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kondo Effect
In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities ( Kondo model). Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Extended to a lattice of ''magnetic impurities'', the Kondo effect likely explains the formation of ''heavy fermions'' and ''Kondo insulators'' in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems. Theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
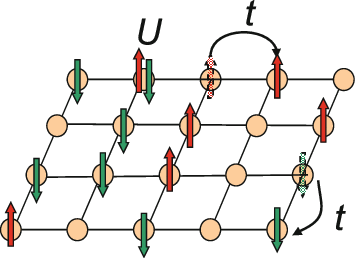
Hubbard Model
The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard (physicist), John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian (quantum mechanics), Hamiltonian thus has two terms: a kinetic term allowing for Quantum tunneling, tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ising Model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent Nuclear magnetic moment, magnetic dipole moments of atomic "spins" that can be in one of two states (+1 or −1). The spins are arranged in a Graph (abstract data type), graph, usually a lattice (group), lattice (where the local structure repeats periodically in all directions), allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases.The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition. Though it is a highly simplified model of a magnetic material, the Ising model can sti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arnoldi Iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of an iterative method. Arnoldi finds an approximation to the eigenvalues and eigenvectors of general (possibly non- Hermitian) matrices by constructing an orthonormal basis of the Krylov subspace, which makes it particularly useful when dealing with large sparse matrices. The Arnoldi method belongs to a class of linear algebra algorithms that give a partial result after a small number of iterations, in contrast to so-called ''direct methods'' which must complete to give any useful results (see for example, Householder transformation). The partial result in this case being the first few vectors of the basis the algorithm is building. When applied to Hermitian matrices it reduces to the Lanczos algorithm. The Arnoldi iteration was invented by W. E. Arnoldi in 1951. Krylov subspaces and the power iteration An intuitive method for finding the largest (in absolute value) ei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |