|
Dehn Invariant
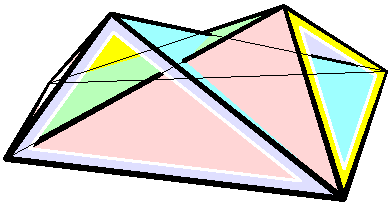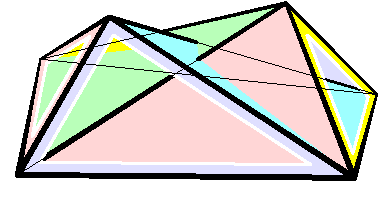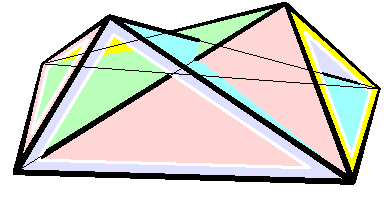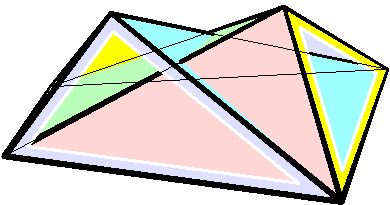
In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled (" dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other. Two polyhedra have a dissection into polyhedral pieces that can be reassembled into either one, if and only if their volumes and Dehn invariants are equal. Having Dehn invariant zero is a necessary (but not sufficient) condition for being a space-filling polyhedron, and a polyhedron can be cut up and reassembled into a space-filling polyhedron if and only if its Dehn invariant is zero. The Dehn invariant of a self-intersection-free flexible polyhedron is invariant as it flexes. Dehn invariants are also an invariant for dissection in higher dimensions, and (with volume) a complete invariant in four dimensions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Third Problem
The third of Hilbert's problems, Hilbert's list of mathematical problems, presented in 1900, was the first to be solved. The problem is related to the following question: given any two polyhedron, polyhedra of equal volume, is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the second? Based on earlier writings by Carl Friedrich Gauss, David Hilbert conjectured that this is not always possible. This was confirmed within the year by his student Max Dehn, who proved that the answer in general is "no" by producing a counterexample. The answer for the analogous question about polygons in 2 dimensions is "yes" and had been known for a long time; this is the Wallace–Bolyai–Gerwien theorem. Unknown to Hilbert and Dehn, Hilbert's third problem was also proposed independently by Władysław Kretkowski for a math contest of 1882 by the Academy of Arts and Sciences of Kraków, and was solved by Ludwik Birkenmajer, Ludwik Antoni B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Product Of Modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps (e.g. multiplication) to be carried out in terms of linear maps. The module construction is analogous to the construction of the tensor product of vector spaces, but can be carried out for a pair of modules over a commutative ring resulting in a third module, and also for a pair of a right-module and a left-module over any ring, with result an abelian group. Tensor products are important in areas of abstract algebra, homological algebra, algebraic topology, algebraic geometry, operator algebras and noncommutative geometry. The universal property of the tensor product of vector spaces extends to more general situations in abstract algebra. The tensor product of an algebra and a module can be used for extension of scalars. For a commutative ring, the tensor product of modules can be iterated to form the tensor algebra of a module, allowing one to define multiplication in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Habilitation
Habilitation is the highest university degree, or the procedure by which it is achieved, in Germany, France, Italy, Poland and some other European and non-English-speaking countries. The candidate fulfills a university's set criteria of excellence in research, teaching, and further education, which usually includes a dissertation. The degree, sometimes abbreviated ''Dr. habil''. (), ''dr hab.'' (), or ''D.Sc.'' ('' Doctor of Sciences'' in Russia and some CIS countries), is often a qualification for full professorship in those countries. In German-speaking countries it allows the degree holder to bear the title ''PD'' (for ). In a number of countries there exists an academic post of docent, appointment to which often requires such a qualification. The degree conferral is usually accompanied by a public oral defence event (a lecture or a colloquium) with one or more opponents. Habilitation is usually awarded 5–15 years after a PhD degree or its equivalent. Achieving this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raoul Bricard
Raoul Bricard (23 March 1870 – 26 November 1943) was a French engineer and a mathematician. He is best known for his work in geometry, especially descriptive geometry and scissors congruence, and kinematics, especially mechanical linkages. Biography Bricard taught geometry at Ecole Centrale des Arts et Manufactures. In 1908 he became a professor of applied geometry at the National Conservatory of Arts and Crafts in Paris. In 1932 he received the Poncelet Prize in mathematics from the Paris Academy of Sciences for his work in geometry. Work In 1896 Bricard published a paper on Hilbert's third problem, even before the problem was stated by Hilbert. In it he proved that mirror symmetric polytopes are scissors congruent, and proved a weak version of Dehn's criterion. In 1897 Bricard published an important investigation on flexible polyhedra. In it he classified all flexible octahedra, now known as Bricard octahedra. This work was the subject of Henri Lebesgue's lectu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Problems
Hilbert's problems are 23 problems in mathematics published by German mathematician David Hilbert in 1900. They were all unsolved at the time, and several proved to be very influential for 20th-century mathematics. Hilbert presented ten of the problems (1, 2, 6, 7, 8, 13, 16, 19, 21, and 22) at the Paris conference of the International Congress of Mathematicians, speaking on August 8 at the Sorbonne. The complete list of 23 problems was published later, in English translation in 1902 by Mary Frances Winston Newson in the ''Bulletin of the American Mathematical Society''. Earlier publications (in the original German) appeared in ''Archiv der Mathematik und Physik''. and Of the cleanly formulated Hilbert problems, numbers 3, 7, 10, 14, 17, 18, 19, 21, and 20 have resolutions that are accepted by consensus of the mathematical community. Problems 1, 2, 5, 6, 9, 11, 12, 15, and 22 have solutions that have partial acceptance, but there exists some controversy as to whether ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Congress Of Mathematicians
The International Congress of Mathematicians (ICM) is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union (IMU). The Fields Medals, the IMU Abacus Medal (known before 2022 as the Nevanlinna Prize), the Carl Friedrich Gauss Prize, Gauss Prize, and the Chern Medal are awarded during the congress's opening ceremony. Each congress is memorialized by a printed set of Proceedings recording academic papers based on invited talks intended to be relevant to current topics of general interest. Being List of International Congresses of Mathematicians Plenary and Invited Speakers, invited to talk at the ICM has been called "the equivalent ... of an induction to a hall of fame". History German mathematicians Felix Klein and Georg Cantor are credited with putting forward the idea of an international congress of mathematicians in the 1890s.A. John Coleman"Mathematics without borders": a book review. ''CMS Notes'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Geometry
Solid geometry or stereometry is the geometry of Three-dimensional space, three-dimensional Euclidean space (3D space). A solid figure is the region (mathematics), region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball (mathematics), ball consists of a sphere and its Interior (topology), interior. Solid geometry deals with the measurements of volumes of various solids, including Pyramid (geometry), pyramids, Prism (geometry), prisms (and other polyhedrons), cubes, Cylinder (geometry), cylinders, cone (geometry), cones (and Frustum, truncated cones). History The Pythagoreanism, Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonism, Platonists. Eudoxus of Cnidus, Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid. ''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the works of earlier mathematicians such as Hippocrates of Chios, Eudoxus of Cnidus and Theaetetus (mathematician), Theaetetus, the ''Elements'' is a collection in 13 books of definitions, postulates, propositions and mathematical proofs that covers plane and solid Euclidean geometry, elementary number theory, and Commensurability (mathematics), incommensurable lines. These include Pythagorean theorem, Thales' theorem, the Euclidean algorithm for greatest common divisors, Euclid's theorem that there are infinitely many prime numbers, and the Compass-and-straightedge construction, construction of regular polygons and Regular polyhedra, polyhedra. Often referred to as the most successful textbook ever written, the ''Elements'' has continued to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert's Axioms
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book ''Grundlagen der Geometrie'' (tr. ''The Foundations of Geometry'') as the foundation for a modern treatment of Euclidean geometry. Other well-known modern axiomatizations of Euclidean geometry are those of Tarski's axioms, Alfred Tarski and of Birkhoff's axioms, George Birkhoff. The axioms Hilbert's axiom system is constructed with six primitive notions: three primitive terms: * Point (geometry), point; * Line (geometry), line; * Plane (mathematics), plane; and three primitive finitary relation, relations: * ''Betweenness'', a ternary relation linking points; * ''Lies on (Containment)'', three binary relations, one linking points and straight lines, one linking points and planes, and one linking straight lines and planes; * ''Congruence'', two binary relations, one linking line segments and one linking angles, each denoted by an infix ≅. Line segments, angles, and triangles may each be d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |