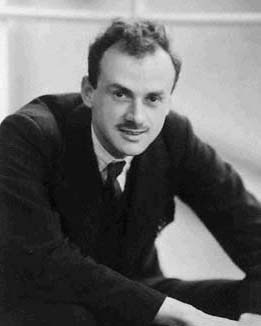|
Darwin Lagrangian
The Darwin Lagrangian (named after Charles Galton Darwin, grandson of Charles Darwin, the naturalist) describes the interaction to order / between two charged particles in a vacuum and is given by L = L_\text + L_\text, where the free particle Lagrangian mechanics, Lagrangian is L_\text = \frac m_1 v_1^2 + \frac m_1 v_1^4 + \frac m_2 v_2^2 + \frac m_2 v_2^4, and the interaction Lagrangian is L_\text = L_\text + L_\text, where the Coulomb force, Coulomb interaction is L_\text = -\frac, and the Charles Galton Darwin, Darwin interaction is L_\text = \frac \frac \mathbf v_1 \cdot \left[\mathbf 1 + \hat\mathbf \hat\mathbf\right] \cdot \mathbf v_2. Here and are the charges on particles 1 and 2 respectively, and are the masses of the particles, and are the velocities of the particles, is the speed of light, is the vector between the two particles, and \hat\mathbf r is the unit vector in the direction of . The free Lagrangian is the Taylor expansion of free Lagrangian of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Galton Darwin
Sir Charles Galton Darwin (19 December 1887 – 31 December 1962) was an English physicist who served as director of the National Physical Laboratory (NPL) during the Second World War. He was a son of the mathematician George Howard Darwin and a grandson of Charles Darwin. Early life Darwin was born at Newnham Grange in Cambridge, England into a scientific dynasty. He was a son of mathematician Sir George Howard Darwin and a grandson of Charles Darwin. His mother was Lady Darwin, Maud du Puy of Philadelphia, Pennsylvania. Darwin's elder sister was the artist Gwen Raverat, and his younger sister Margaret married Geoffrey Keynes, the brother of the economist John Maynard Keynes. His younger brother William Robert Darwin was a London stockbroker. Darwin was educated at Marlborough College (1901–1906) and then studied mathematics at Trinity College, Cambridge, graduating BA in 1910, later promoted to MA by seniority. Career He secured a post-graduate position at the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational ( curl-free) vector field and a solenoidal (divergence-free) vector field; this is known as the Helmholtz decomposition or Helmholtz representation. It is named after Hermann von Helmholtz. As an irrotational vector field has a scalar potential and a solenoidal vector field has a vector potential, the Helmholtz decomposition states that a vector field (satisfying appropriate smoothness and decay conditions) can be decomposed as the sum of the form -\nabla \phi + \nabla \times \mathbf, where \phi is a scalar field called "scalar potential", and is a vector field, called a vector potential. Statement of the theorem Let \mathbf be a vector field on a bounded domain V\subseteq\mathbb^3, which is twice continuou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Static Forces And Virtual-particle Exchange
Static force fields are fields, such as a simple electric, magnetic or gravitational fields, that exist without excitations. The most common approximation method that physicists use for scattering calculations can be interpreted as static forces arising from the interactions between two bodies mediated by virtual particles, particles that exist for only a short time determined by the uncertainty principle. The virtual particles, also known as force carriers, are bosons, with different bosons associated with each force. The virtual-particle description of static forces is capable of identifying the spatial form of the forces, such as the inverse-square behavior in Newton's law of universal gravitation and in Coulomb's law. It is also able to predict whether the forces are attractive or repulsive for like bodies. The path integral formulation is the natural language for describing force carriers. This article uses the path integral formulation to describe the force carriers fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Electrodynamics
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction. In technical terms, QED can be described as a perturbation theory of the electromagnetic quantum vacuum. Richard Feynman called it "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen. History The first formulation of a quantum theory describing radiation and matter interaction is attributed to British scientist Paul Dirac, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wheeler–Feynman Absorber Theory
The Wheeler–Feynman absorber theory (also called the Wheeler–Feynman time-symmetric theory), named after its originators, the physicists Richard Feynman and John Archibald Wheeler, is an interpretation of electrodynamics derived from the assumption that the solutions of the electromagnetic field equations must be invariant under time-reversal transformation, as are the field equations themselves. Indeed, there is no apparent reason for the time-reversal symmetry breaking, which singles out a preferential time direction and thus makes a distinction between past and future. A time-reversal invariant theory is more logical and elegant. Another key principle, resulting from this interpretation and reminiscent of Mach's principle due to Hugo Tetrode, is that elementary particles are not self-interacting. This immediately removes the problem of self-energies. T-symmetry and causality The requirement of time-reversal symmetry, in general, is difficult to reconcile with the princ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Breit Equation
The Breit equation is a relativistic wave equation derived by Gregory Breit in 1929 based on the Dirac equation, which formally describes two or more massive spin-1/2 particles (electrons, for example) interacting electromagnetically to the first order in perturbation theory. It accounts for magnetic interactions and retardation effects to the order of ''1/c2''. When other quantum electrodynamic effects are negligible, this equation has been shown to give results in good agreement with experiment. It was originally derived from the Darwin Lagrangian but later vindicated by the Wheeler–Feynman absorber theory and eventually quantum electrodynamics. Introduction The Breit equation is not only an approximation in terms of quantum mechanics, but also in terms of relativity theory as it is not completely invariant with respect to the Lorentz transformation. Just as does the Dirac equation, it treats nuclei as point sources of an external field for the particles it describes. For ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Transformation
In mathematics, the Legendre transformation (or Legendre transform), named after Adrien-Marie Legendre, is an involutive transformation on real-valued convex functions of one real variable. In physical problems, it is used to convert functions of one quantity (such as velocity, pressure, or temperature) into functions of the conjugate quantity (momentum, volume, and entropy, respectively). In this way, it is commonly used in classical mechanics to derive the Hamiltonian formalism out of the Lagrangian formalism (or vice versa) and in thermodynamics to derive the thermodynamic potentials, as well as in the solution of differential equations of several variables. For sufficiently smooth functions on the real line, the Legendre transform f^* of a function f can be specified, up to an additive constant, by the condition that the functions' first derivatives are inverse functions of each other. This can be expressed in Euler's derivative notation as Df(\cdot) = \left( D f^* \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Mechanics
Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a link between classical and quantum mechanics. Overview Phase space coordinates (p,q) and Hamiltonian H Let (M, \mathcal L) be a mechanical system with the configuration space M and the smooth Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''momenta''. (Also ''generalized momenta'', ''conjugate momenta'', and ''canonical momenta''). For a time instant t, the Legendre transfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations Of Motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time.''Encyclopaedia of Physics'' (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3 More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system.''Analytical Mechanics'', L.N. Hand, J.D. Finch, Cambridge University Press, 2008, The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector field flux behaves like a source at a given point. It is a local measure of its "outgoingness" – the extent t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |