Graph Rewriting

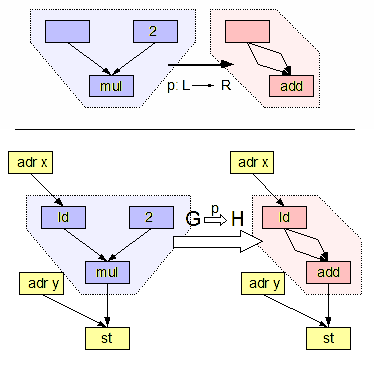
picture info	Graph Rewriting In computer science, graph transformation, or graph rewriting, concerns the technique of creating a new graph out of an original graph algorithmically. It has numerous applications, ranging from software engineering ( software construction and also software verification) to layout algorithms and picture generation. Graph transformations can be used as a computation abstraction. The basic idea is that if the state of a computation can be represented as a graph, further steps in that computation can then be represented as transformation rules on that graph. Such rules consist of an original graph, which is to be matched to a subgraph in the complete state, and a replacing graph, which will replace the matched subgraph. Formally, a graph rewriting system usually consists of a set of graph rewrite rules of the form L \rightarrow R, with L being called pattern graph (or left-hand side) and R being called replacement graph (or right-hand side of the rule). A graph rewrite rule is applie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Computer Science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Injective In mathematics, an injective function (also known as injection, or one-to-one function ) is a function that maps distinct elements of its domain to distinct elements of its codomain; that is, implies (equivalently by contraposition, implies ). In other words, every element of the function's codomain is the image of one element of its domain. The term must not be confused with that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain. A homomorphism between algebraic structures is a function that is compatible with the operations of the structures. For all common algebraic structures, and, in particular for vector spaces, an is also called a . However, in the more general context of category theory, the definition of a monomorphism differs from that of an injective homomorphism. This is thus a theorem that they are equivalent for algebraic structures; see for more details. A func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Double-pushout Approach In computer science, double pushout graph rewriting (or DPO graph rewriting) refers to a mathematical framework for graph rewriting. It was introduced as one of the first algebraic approaches to graph rewriting in the article "Graph-grammars: An algebraic approach" (1973). It has since been generalized to allow rewriting structures which are not graphs, and to handle negative application conditions, among other extensions. Definition A DPO graph transformation system (or graph grammar) consists of a finite graph, which is the starting state, and a finite or countable set of labeled spans in the category of finite graphs and graph homomorphisms, which serve as derivation rules. The rule spans are generally taken to be composed of monomorphisms, but the details can vary."Double-pushout graph transformation revisited", Habel, Annegret and Müller, Jürgen and Plump, Detlef, Mathematical Structures in Computer Science, vol. 11, no. 05., pp. 637--688, 2001, Cambridge University Press ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Single-pushout Approach In computer science, a single pushout graph rewriting or SPO graph rewriting refers to a mathematical framework for graph rewriting, and is used in contrast to the double-pushout approach In computer science, double pushout graph rewriting (or DPO graph rewriting) refers to a mathematical framework for graph rewriting. It was introduced as one of the first algebraic approaches to graph rewriting in the article "Graph-grammars: An al ... of graph rewriting. References Further reading * Graph rewriting {{graph-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Attributed Graph Grammar In computer science, an attributed graph grammar is a class of graph grammar that associates vertices with a set of attributes and rewrites with functions on attributes. In the algebraic approach to graph grammars, they are usually formulated using the double-pushout approach or the single-pushout approach. Implementation AGG, a rule-based visual language that directly expresses attributed graph grammars using the single-pushout approach has been developed at TU Berlin for many years. See also * Graph rewriting * Attribute grammar An attribute grammar is a formal way to supplement a formal grammar with semantic information processing. Semantic information is stored in attributes associated with terminal and nonterminal symbols of the grammar. The values of attributes are t ... Notes References . Ehrig, Heckel, Korff, Lowe, Ribeiro, Wagner and Corradini, 1997. Algebraic Approaches to Graph Transformation - Part II: Single Pushout Approach and Comparison with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Automated Verification In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics. Formal verification is a key incentive for formal specification of systems, and is at the core of formal methods. It represents an important dimension of analysis and verification in electronic design automation and is one approach to software verification. The use of formal verification enables the highest Evaluation Assurance Level ( EAL7) in the framework of common criteria for computer security certification. Formal verification can be helpful in proving the correctness of systems such as: cryptographic protocols, combinational circuits, digital circuits with internal memory, and software expressed as source code in a programming language. Prominent examples of verified software systems include the CompCert verified C compiler and the seL4 h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Operational Semantics Operational semantics is a category of formal programming language semantics in which certain desired properties of a program, such as correctness, safety or security, are verified by constructing proofs from logical statements about its execution and procedures, rather than by attaching mathematical meanings to its terms (denotational semantics). Operational semantics are classified in two categories: structural operational semantics (or small-step semantics) formally describe how the ''individual steps'' of a computation take place in a computer-based system; by opposition natural semantics (or big-step semantics) describe how the ''overall results'' of the executions are obtained. Other approaches to providing a formal semantics of programming languages include axiomatic semantics and denotational semantics. The operational semantics for a programming language describes how a valid program is interpreted as sequences of computational steps. These sequences then ''are'' the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]