|
Attributed Graph Grammar
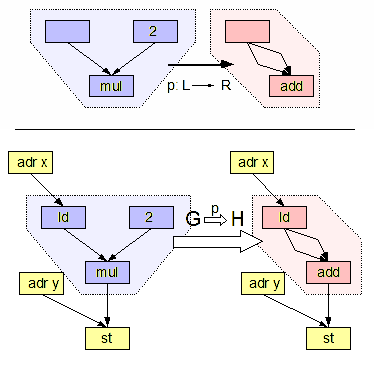
In computer science, an attributed graph grammar is a class of graph grammar that associates vertices with a set of attributes and rewrites with functions on attributes. In the algebraic approach to graph grammars, they are usually formulated using the double-pushout approach or the single-pushout approach. Implementation AGG, a rule-based visual language that directly expresses attributed graph grammars using the single-pushout approach has been developed at TU Berlin The Technical University of Berlin (official name both in English and german: link=no, Technische Universität Berlin, also known as TU Berlin and Berlin Institute of Technology) is a public research university located in Berlin, Germany. It was ... for many years. Notes References *{{citation, first=Grzegorz, last=Rozenberg, title=Handbook of Graph Grammars and Computing by Graph Transformations, publisher=World Scientific Publishing, volumes 1–3, year=1997, isbn=9810228848, url=http://www.informatik.uni-tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (including the design and implementation of hardware and software). Computer science is generally considered an area of academic research and distinct from computer programming. Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and for preventing security vulnerabilities. Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of repositories ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Grammar
In computer science, graph transformation, or graph rewriting, concerns the technique of creating a new graph (discrete mathematics), graph out of an original graph algorithmically. It has numerous applications, ranging from software engineering (software construction and also Formal verification, software verification) to layout algorithms and picture generation. Graph transformations can be used as a computation abstraction. The basic idea is that if the state of a computation can be represented as a graph, further steps in that computation can then be represented as transformation rules on that graph. Such rules consist of an original graph, which is to be matched to a subgraph in the complete state, and a replacing graph, which will replace the matched subgraph. Formally, a graph rewriting system usually consists of a set of graph rewrite rules of the form L \rightarrow R, with L being called pattern graph (or left-hand side) and R being called replacement graph (or right-hand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double-pushout Approach
In computer science, double pushout graph rewriting (or DPO graph rewriting) refers to a mathematical framework for graph rewriting. It was introduced as one of the first algebraic approaches to graph rewriting in the article "Graph-grammars: An algebraic approach" (1973). It has since been generalized to allow rewriting structures which are not graphs, and to handle negative application conditions, among other extensions. Definition A DPO graph transformation system (or graph grammar) consists of a finite graph, which is the starting state, and a finite or countable set of labeled spans in the category of finite graphs and graph homomorphisms, which serve as derivation rules. The rule spans are generally taken to be composed of monomorphisms, but the details can vary."Double-pushout graph transformation revisited", Habel, Annegret and Müller, Jürgen and Plump, Detlef, Mathematical Structures in Computer Science, vol. 11, no. 05., pp. 637--688, 2001, Cambridge University Press ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-pushout Approach
In computer science, a single pushout graph rewriting or SPO graph rewriting refers to a mathematical framework for graph rewriting, and is used in contrast to the double-pushout approach In computer science, double pushout graph rewriting (or DPO graph rewriting) refers to a mathematical framework for graph rewriting. It was introduced as one of the first algebraic approaches to graph rewriting in the article "Graph-grammars: An al ... of graph rewriting. References Further reading * Graph rewriting {{compu-sci-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TU Berlin
The Technical University of Berlin (official name both in English and german: link=no, Technische Universität Berlin, also known as TU Berlin and Berlin Institute of Technology) is a public research university located in Berlin, Germany. It was the first German university to adopt the name "Technische Universität" (Technical University). The university alumni and professor list includes several US National Academies members, two National Medal of Science laureates and ten Nobel Prize laureates. TU Berlin is a member of TU9, an incorporated society of the largest and most notable German institutes of technology and of the Top International Managers in Engineering network, which allows for student exchanges between leading engineering schools. It belongs to the Conference of European Schools for Advanced Engineering Education and Research. The TU Berlin is home of two innovation centers designated by the European Institute of Innovation and Technology. The university is label ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
