|
Cosmic Censorship Hypothesis
The weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of gravitational singularities arising in general relativity. Singularities that arise in the solutions of Einstein's equations are typically hidden within event horizons, and therefore cannot be observed from the rest of spacetime. Singularities that are not so hidden are called ''naked''. The weak cosmic censorship hypothesis was conceived by Roger Penrose in 1969 and posits that no naked singularities exist in the universe. Basics Since the physical behavior of singularities is unknown, if singularities can be observed from the rest of spacetime, causality may break down, and physics may lose its predictive power. The issue cannot be avoided, since according to the Penrose–Hawking singularity theorems, singularities are inevitable in physically reasonable situations. Still, in the absence of naked singularities, the universe, as described by the general theory of rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), have shaped much of mathematical history as new areas of mathematics are developed in order to prove them. Resolution of conjectures Proof Formal mathematics is based on ''provable'' truth. In mathematics, any number of cases supporting a universally quantified conjecture, no matter how large, is insufficient for establishing the conjecture's veracity, since a single counterexample could immediately bring down the conjecture. Mathematical journals sometimes publish the minor results of research teams having extended the search for a counterexample farther than previously done. For instance, the Collatz conjecture, which concerns whether or not certain sequences of integers terminate, has been tested for all integers up to 1.2 × 101 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Surface
In the mathematical field of Lorentzian geometry, a Cauchy surface is a certain kind of submanifold of a Lorentzian manifold. In the application of Lorentzian geometry to the physics of general relativity, a Cauchy surface is usually interpreted as defining an "instant of time". In the mathematics of general relativity, Cauchy surfaces provide boundary conditions for the causal structure in which the Einstein equations can be solved (using, for example, the ADM formalism.) They are named for French mathematician Augustin-Louis Cauchy (1789–1857) due to their relevance for the Cauchy problem of general relativity. Informal introduction Although it is usually phrased in terms of general relativity, the formal notion of a Cauchy surface can be understood in familiar terms. Suppose that humans can travel at a maximum speed of 20 miles per hour. This places constraints, for any given person, upon where they can reach by a certain time. For instance, it is impossible for a person wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbits
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an physical body, object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an satellite, artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the barycenter, center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains Newton's law of universal gravitation, gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
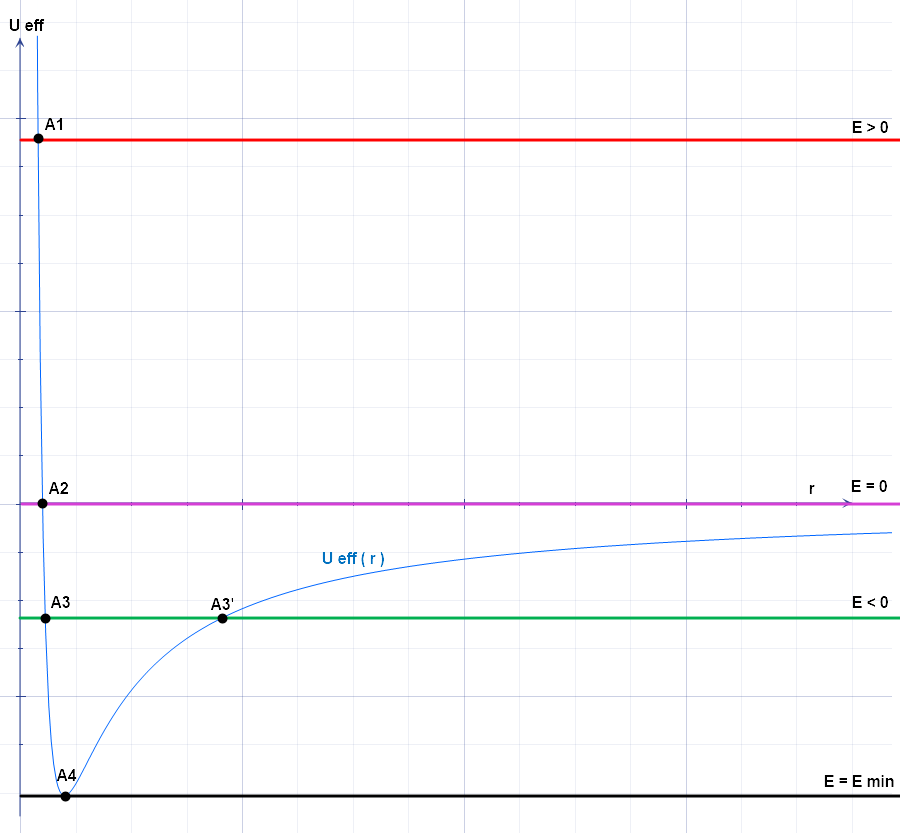
Effective Potential
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the "opposing" centrifugal potential energy with the potential energy of a dynamical system. It may be used to determine the orbits of planets (both Newtonian and relativistic) and to perform semi-classical atomic calculations, and often allows problems to be reduced to fewer dimensions. Definition The basic form of potential U_\text is defined as U_\text(\mathbf) = \frac + U(\mathbf), where : ''L'' is the angular momentum, : ''r'' is the distance between the two masses, : ''μ'' is the reduced mass of the two bodies (approximately equal to the mass of the orbiting body if one mass is much larger than the other), : ''U''(''r'') is the general form of the potential. The effective force, then, is the negative gradient of the effective potential: \begin \mathbf_\text &= -\nabla U_\text(\mathbf) \\ &= \fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quanta Magazine
''Quanta Magazine'' is an editorially independent online publication of the Simons Foundation covering developments in physics, mathematics, biology and computer science. History ''Quanta Magazine'' was initially launched as ''Simons Science News'' in October 2012, but it was renamed to its current title in July 2013. It was founded by the former ''New York Times'' journalist Thomas Lin, who was the magazine's editor-in-chief until 2024. The two deputy editors are John Rennie and Michael Moyer, formerly of ''Scientific American'', and the art director is Samuel Velasco. In 2024, Samir Patel became the magazine's second editor in chief. Content The articles in the magazine are freely available to read online. ''Scientific American'', ''Wired'', ''The Atlantic'', and ''The Washington Post'', as well as international science publications like '' Spektrum der Wissenschaft'', have reprinted articles from the magazine. In November 2018, MIT Press The MIT Press is the uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr Metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Horizon
In physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem (a particular boundary value problem of the theory of partial differential equations). One side of the horizon contains closed space-like geodesics and the other side contains closed time-like geodesics. The concept is named after Augustin-Louis Cauchy. Under the averaged weak energy condition (AWEC), Cauchy horizons are inherently unstable. However, cases of AWEC violation, such as the Casimir effect caused by periodic boundary conditions, do exist, and since the region of spacetime inside the Cauchy horizon has closed timelike curves it is subject to periodic boundary conditions. If the spacetime inside the Cauchy horizon violates AWEC, then the horizon becomes stable and frequency boosting effects would be canceled out by the tendency of the spacetime to act as a divergent lens. Were this conjecture to be shown empirically true, it would provide a counter-example to the stro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentzian Manifold
In mathematical physics, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere non-degenerate bilinear form, nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of Positive-definite bilinear form, positive-definiteness is relaxed. Every tangent space of a pseudo-Riemannian manifold is a pseudo-Euclidean vector space. A special case used in general relativity is a four-dimensional Lorentzian manifold for modeling spacetime, where tangent vectors can be classified as Causal structure, timelike, null, and spacelike. Introduction Manifolds In differential geometry, a differentiable manifold is a space that is locally similar to a Euclidean space. In an ''n''-dimensional Euclidean space any point can be specified by ''n'' real numbers. These are called the coordinates of the point. An ''n''-dimensional differentiable manifold is a generalisation of '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causal Structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the possible causal relationships between points in the manifold. Lorentzian manifolds can be classified according to the types of causal structures they admit (''causality conditions''). Introduction In modern physics (especially general relativity) spacetime is represented by a Lorentzian manifold. The causal relations between points in the manifold are interpreted as describing which events in spacetime can influence which other events. The causal structure of an arbitrary (possibly curved) Lorentzian manifold is made more complicated by the presence of curvature. Discussions of the causal structure for such manifolds must be phrased in terms of smooth curves joining pairs of points. Conditions on the tangent vectors of the curves then define the causal relationships. Tangent vectors If \,(M,g) is a Lorentzian manifold (for metric g on manifold M) then the nonzero tangent vectors at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Infinity
In theoretical physics, null infinity is a region at the boundary of asymptotically flat spacetimes. In general relativity, straight paths in spacetime, called geodesics, may be space-like, time-like, or light-like (also called null). The distinction between these paths stems from whether the Spacetime Interval, spacetime interval of the path is positive (corresponding to space-like), negative (corresponding to time-like), or zero (corresponding to null). Light-like paths physically correspond to physical phenomena which propagate through space at the speed of light, such as electromagnetic radiation and Gravitational wave, gravitational radiation. The boundary of a flat spacetime is known as conformal infinity, and can be thought of as the end points of all geodesics as they go off to infinity. The region of null infinity corresponds to the terminus of all null geodesics in a flat Minkowski space. The different regions of conformal infinity are most often visualized on a Penrose dia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The New York Times
''The New York Times'' (''NYT'') is an American daily newspaper based in New York City. ''The New York Times'' covers domestic, national, and international news, and publishes opinion pieces, investigative reports, and reviews. As one of the longest-running newspapers in the United States, the ''Times'' serves as one of the country's Newspaper of record, newspapers of record. , ''The New York Times'' had 9.13 million total and 8.83 million online subscribers, both by significant margins the List of newspapers in the United States, highest numbers for any newspaper in the United States; the total also included 296,330 print subscribers, making the ''Times'' the second-largest newspaper by print circulation in the United States, following ''The Wall Street Journal'', also based in New York City. ''The New York Times'' is published by the New York Times Company; since 1896, the company has been chaired by the Ochs-Sulzberger family, whose current chairman and the paper's publ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Falsifiable
Falsifiability (or refutability) is a deductive standard of evaluation of scientific theories and hypotheses, introduced by the philosopher of science Karl Popper in his book '' The Logic of Scientific Discovery'' (1934). A theory or hypothesis is falsifiable if it can be logically contradicted by an empirical test. Popper emphasized the asymmetry created by the relation of a universal law with basic observation statements and contrasted falsifiability to the intuitively similar concept of ''verifiability'' that was then current in logical positivism. He argued that the only way to verify a claim such as "All swans are white" would be if one could theoretically observe all swans, which is not possible. On the other hand, the falsifiability requirement for an anomalous instance, such as the observation of a single black swan, is theoretically reasonable and sufficient to logically falsify the claim. Popper proposed falsifiability as the cornerstone solution to both the probl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |