|
Correlation Coefficient
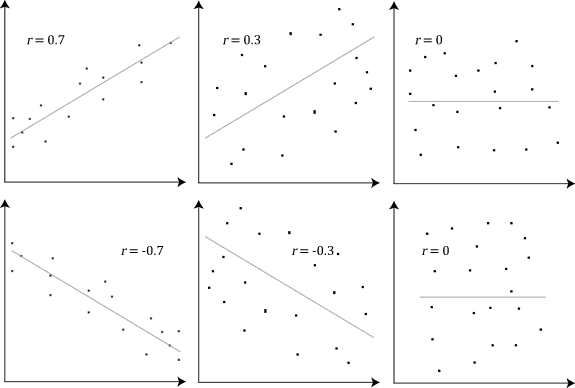
A correlation coefficient is a numerical measure of some type of linear correlation, meaning a statistical relationship between two variables. The variables may be two columns of a given data set of observations, often called a sample, or two components of a multivariate random variable with a known distribution. Several types of correlation coefficient exist, each with their own definition and own range of usability and characteristics. They all assume values in the range from −1 to +1, where ±1 indicates the strongest possible correlation and 0 indicates no correlation. As tools of analysis, correlation coefficients present certain problems, including the propensity of some types to be distorted by outliers and the possibility of incorrectly being used to infer a causal relationship between the variables (for more, see Correlation does not imply causation). Types There are several different measures for the degree of correlation in data, depending on the kind of data: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Numerical Measure
Measurement is the quantification (science), quantification of variable and attribute (research), attributes of an object or event, which can be used to compare with other objects or events. In other words, measurement is a process of determining how large or small a physical quantity is as compared to a basic reference quantity of the same kind. The scope and application of measurement are dependent on the context and discipline. In natural sciences and engineering, measurements do not apply to Level of measurement#Nominal level, nominal properties of objects or events, which is consistent with the guidelines of the International Vocabulary of Metrology (VIM) published by the International Bureau of Weights and Measures (BIPM). However, in other fields such as statistics as well as the Social Sciences, social and behavioural sciences, measurements can have Level of measurement, multiple levels, which would include nominal, ordinal, interval and ratio scales. Measurement is a co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Intraclass Correlation
In statistics, the intraclass correlation, or the intraclass correlation coefficient (ICC), is a descriptive statistic that can be used when quantitative measurements are made on units that are organized into groups. It describes how strongly units in the same group resemble each other. While it is viewed as a type of correlation, unlike most other correlation measures, it operates on data structured as groups rather than data structured as paired observations. The ''intraclass correlation'' is commonly used to quantify the degree to which individuals with a fixed degree of relatedness (e.g. full siblings) resemble each other in terms of a quantitative trait (see heritability). Another prominent application is the assessment of consistency or reproducibility of quantitative measurements made by different observers measuring the same quantity. Early ICC definition: unbiased but complex formula The earliest work on intraclass correlations focused on the case of paired measu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Goodness Of Fit
The goodness of fit of a statistical model describes how well it fits a set of observations. Measures of goodness of fit typically summarize the discrepancy between observed values and the values expected under the model in question. Such measures can be used in statistical hypothesis testing, e.g. to test for normality of residuals, to test whether two samples are drawn from identical distributions (see Kolmogorov–Smirnov test), or whether outcome frequencies follow a specified distribution (see Pearson's chi-square test). In the analysis of variance, one of the components into which the variance is partitioned may be a lack-of-fit sum of squares. Fit of distributions In assessing whether a given distribution is suited to a data-set, the following tests and their underlying measures of fit can be used: * Bayesian information criterion * Kolmogorov–Smirnov test * Cramér–von Mises criterion * Anderson–Darling test * Berk-Jones tests * Shapiro–Wilk test * Chi-s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Distance Correlation
In statistics and in probability theory, distance correlation or distance covariance is a measure of dependence between two paired random vectors of arbitrary, not necessarily equal, dimension. The population distance correlation coefficient is zero if and only if the random vectors are independent. Thus, distance correlation measures both linear and nonlinear association between two random variables or random vectors. This is in contrast to Pearson's correlation, which can only detect linear association between two random variables. Distance correlation can be used to perform a statistical test of dependence with a permutation test. One first computes the distance correlation (involving the re-centering of Euclidean distance matrices) between two random vectors, and then compares this value to the distance correlations of many shuffles of the data. Background The classical measure of dependence, the Pearson correlation coefficient, is mainly sensitive to a linear relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Correlation Ratio
In statistics, the correlation ratio is a measure of the curvilinear relationship between the statistical dispersion within individual categories and the dispersion across the whole population or sample. The measure is defined as the ''ratio'' of two standard deviations representing these types of variation. The context here is the same as that of the intraclass correlation coefficient, whose value is the square of the correlation ratio. Definition Suppose each observation is ''yxi'' where ''x'' indicates the category that observation is in and ''i'' is the label of the particular observation. Let ''nx'' be the number of observations in category ''x'' and :\overline_x=\frac and \overline=\frac, where \overline_x is the mean of the category ''x'' and \overline is the mean of the whole population. The correlation ratio η (eta) is defined as to satisfy :\eta^2 = \frac which can be written as :\eta^2 = \frac, \text^2 = \frac \text ^2 = \frac, i.e. the weighted variance of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Correlation And Dependence
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Coefficient Of Determination
In statistics, the coefficient of determination, denoted ''R''2 or ''r''2 and pronounced "R squared", is the proportion of the variation in the dependent variable that is predictable from the independent variable(s). It is a statistic used in the context of statistical models whose main purpose is either the prediction of future outcomes or the testing of hypotheses, on the basis of other related information. It provides a measure of how well observed outcomes are replicated by the model, based on the proportion of total variation of outcomes explained by the model. There are several definitions of ''R''2 that are only sometimes equivalent. In simple linear regression (which includes an intercept), ''r''2 is simply the square of the sample ''correlation coefficient'' (''r''), between the observed outcomes and the observed predictor values. If additional regressors are included, ''R''2 is the square of the '' coefficient of multiple correlation''. In both such cases, the coeffi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Correlation Disattenuation
Regression dilution, also known as regression attenuation, is the biasing of the linear regression slope towards zero (the underestimation of its absolute value), caused by errors in the independent variable. Consider fitting a straight line for the relationship of an outcome variable ''y'' to a predictor variable ''x'', and estimating the slope of the line. Statistical variability, measurement error or random noise in the ''y'' variable causes uncertainty in the estimated slope, but not bias: on average, the procedure calculates the right slope. However, variability, measurement error or random noise in the ''x'' variable causes bias in the estimated slope (as well as imprecision). The greater the variance in the ''x'' measurement, the closer the estimated slope must approach zero instead of the true value. It may seem counter-intuitive that noise in the predictor variable ''x'' induces a bias, but noise in the outcome variable ''y'' does not. Recall that linear regression is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Dichotomous Variable
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. In computer science and some branches of mathematics, categorical variables are referred to as enumerations or enumerated types. Commonly (though not in this article), each of the possible values of a categorical variable is referred to as a level. The probability distribution associated with a random categorical variable is called a categorical distribution. Categorical data is the statistical data type consisting of categorical variables or of data that has been converted into that form, for example as grouped data. More specifically, categorical data may derive from observations made of qualitative data that are summarised as counts or cross tabulations, or from observation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value. Definitions Notation and parametrization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Polychoric Correlation
In statistics, polychoric correlation{{Cite web, url=https://support.sas.com/documentation/cdl/en/procstat/65543/HTML/default/viewer.htm#procstat_corr_details14.htm, title=Base SAS(R) 9.3 Procedures Guide: Statistical Procedures, Second Edition, website=support.sas.com, language=en, access-date=2018-01-10 is a technique for estimating the correlation between two hypothesised normally distributed continuous latent variables, from two observed ordinal variables. Tetrachoric correlation is a special case of the polychoric correlation applicable when both observed variables are dichotomous. These names derive from the polychoric and tetrachoric series which are used for estimation of these correlations. Applications and examples This technique is frequently applied when analysing items on self-report instruments such as personality tests and surveys that often use rating scales with a small number of response options (e.g., strongly disagree to strongly agree). The smaller the numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |