|
Coolfluid
{{Infobox software , name = COOLFluiD , logo = , screenshot = , caption = , author = , developer = von Karman Institute and others , released = , latest release version = 2014.9 , latest release date = 23 09 2014 , operating system = Unix/Linux/Microsoft Windows, Windows/Mac OS X , genre = , license = [LGPLv3] , website COOLFluiD on GitHub COOLFluiD is a component based scientific computing environment that handles High performance computing, high-performance computing problems with focus on complex computational fluid dynamics (CFD) involving multiphysics phenomena. It features a ''Collaborative Simulation Environment'' where multiple physical models and multiple discretization methods are implemented as components within the environment. These components form a component-based architecture where they s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical models, mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential. The FEM is a general numerical analysis, numerical method for solving partial differential equations in two or three space variables (i.e., some boundary value problems). To solve a problem, the FEM subdivides a large system into smaller, simpler parts that are called finite elements. This is achieved by a particular space discretization in the space dimensions, which is implemented by the construction of a Types of mesh, mesh of the object: the numerical domain for the solution, which has a finite number of points. The finite element method formulation of a boundary value problem finally results in a system of algebraic equations. The method approxi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
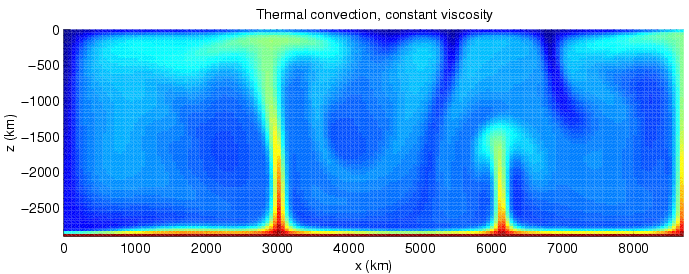
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, at which point they are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrochemistry
Electrochemistry is the branch of physical chemistry concerned with the relationship between electrical potential difference, as a measurable and quantitative phenomenon, and identifiable chemical change, with the potential difference as an outcome of a particular chemical change, or vice versa. These reactions involve electrons moving via an electronically-conducting phase (typically an external electrical circuit, but not necessarily, as in electroless plating) between electrodes separated by an ionically conducting and electronically insulating electrolyte (or ionic species in a solution). When a chemical reaction is driven by an electrical potential difference, as in electrolysis, or if a potential difference results from a chemical reaction as in an electric battery or fuel cell, it is called an ''electrochemical'' reaction. Unlike in other chemical reactions, in electrochemical reactions electrons are not transferred directly between atoms, ions, or molecules, but via ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetohydrodynamics
Magnetohydrodynamics (MHD; also called magneto-fluid dynamics or hydromagnetics) is the study of the magnetic properties and behaviour of electrically conducting fluids. Examples of such magnetofluids include plasmas, liquid metals, salt water, and electrolytes. The word ''magnetohydrodynamics'' is derived from ' meaning magnetic field, ' meaning water, and ' meaning movement. The field of MHD was initiated by Hannes Alfvén, for which he received the Nobel Prize in Physics in 1970. The fundamental concept behind MHD is that magnetic fields can induce currents in a moving conductive fluid, which in turn polarizes the fluid and reciprocally changes the magnetic field itself. The set of equations that describe MHD are a combination of the Navier–Stokes equations of fluid dynamics and Maxwell’s equations of electromagnetism. These differential equations must be solved simultaneously, either analytically or numerically. History The first r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aeroacoustics
Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects. Although no complete scientific theory of the generation of noise by aerodynamic flows has been established, most practical aeroacoustic analysis relies upon the so-called ''aeroacoustic analogy'', proposed by Sir James Lighthill in the 1950s while at the University of Manchester. whereby the governing equations of motion of the fluid are coerced into a form reminiscent of the wave equation of "classical" (i.e. linear) acoustics in the left-hand side with the remaining terms as sources in the right-hand side. History The modern discipline of aeroacoustics can be said to have originated with the first publication of Lighthill in the early 1950s, when noise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Aeroacoustics
Computational aeroacoustics is a branch of aeroacoustics that aims to analyze the generation of noise by turbulent flows through numerical methods. History The origin of computational aeroacoustics can only very likely be dated back to the middle of the 1980s, with a publication of Hardin and Lamkin who claimed, that "'' ..the field of computational fluid mechanics has been advancing rapidly in the past few years and now offers the hope that "computational aeroacoustics," where noise is computed directly from a first principles determination of continuous velocity and vorticity fields, might be possible, ..'" Later in a publication 1986 the same authors introduced the abbreviation CAA. The term was initially used for a low Mach number approach (Expansion of the acoustic perturbation field about an incompressible flow) as it is described under EIF. Later in the beginning 1990s the growing CAA community picked up the term and extensively used it for any kind of numerical method d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible Flow
In fluid mechanics or more generally continuum mechanics, incompressible flow ( isochoric flow) refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero (see the derivation below, which illustrates why these conditions are equivalent). Incompressible flow does not imply that the fluid itself is incompressible. It is shown in the derivation below that (under the right conditions) even compressible fluids can – to a good approximation – be modelled as an incompressible flow. Incompressible flow implies that the density remains constant within a parcel of fluid that moves with the flow velocity. Derivation The fundamental requirement for incompressible flow is that the density, \rho , is constant within a small element volume, ''dV'', which moves at the flow velocity u. Mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discontinuous Galerkin Method
In applied mathematics, discontinuous Galerkin methods (DG methods) form a class of numerical methods for solving differential equations. They combine features of the finite element and the finite volume framework and have been successfully applied to hyperbolic, elliptic, parabolic and mixed form problems arising from a wide range of applications. DG methods have in particular received considerable interest for problems with a dominant first-order part, e.g. in electrodynamics, fluid mechanics and plasma physics. Discontinuous Galerkin methods were first proposed and analyzed in the early 1970s as a technique to numerically solve partial differential equations. In 1973 Reed and Hill introduced a DG method to solve the hyperbolic neutron transport equation. The origin of the DG method for elliptic problems cannot be traced back to a single publication as features such as jump penalization in the modern sense were developed gradually. However, among the early influential contribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residual (numerical Analysis)
Loosely speaking, a residual is the error in a result. To be precise, suppose we want to find ''x'' such that : f(x)=b. Given an approximation ''x''0 of ''x'', the residual is : b - f(x_0) that is, "what is left of the right hand side" after subtracting ''f''(''x''0)" (thus, the name "residual": what is left, the rest). On the other hand, the error is : x - x_0 If the exact value of ''x'' is not known, the residual can be computed, whereas the error cannot. Residual of the approximation of a function Similar terminology is used dealing with differential, integral and functional equations. For the approximation f_\text of the solution f of the equation : T(f)(x)=g(x) \, , the residual can either be the function : ~g(x)~ - ~T(f_\text)(x) or can be said to be the maximum of the norm of this difference : \max_ , g(x)-T(f_\text)(x), over the domain \mathcal X, where the function f_\text is expected to approximate the solution f , or some integral of a function of the differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unix
Unix (; trademarked as UNIX) is a family of multitasking, multiuser computer operating systems that derive from the original AT&T Unix, whose development started in 1969 at the Bell Labs research center by Ken Thompson, Dennis Ritchie, and others. Initially intended for use inside the Bell System, AT&T licensed Unix to outside parties in the late 1970s, leading to a variety of both academic and commercial Unix variants from vendors including University of California, Berkeley ( BSD), Microsoft ( Xenix), Sun Microsystems (SunOS/ Solaris), HP/ HPE (HP-UX), and IBM ( AIX). In the early 1990s, AT&T sold its rights in Unix to Novell, which then sold the UNIX trademark to The Open Group, an industry consortium founded in 1996. The Open Group allows the use of the mark for certified operating systems that comply with the Single UNIX Specification (SUS). Unix systems are characterized by a modular design that is sometimes called the " Unix philosophy". According to this p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |