|
Continuous Fast Multipole Method
__NOTOC__ The fast multipole method (FMM) is a numerical technique that was developed to speed up the calculation of long-ranged forces in the ''n''-body problem. It does this by expanding the system Green's function using a multipole expansion, which allows one to group sources that lie close together and treat them as if they are a single source. The FMM has also been applied in accelerating the iterative solver in the method of moments (MOM) as applied to computational electromagnetics problems, and in particular in computational bioelectromagnetism. The FMM was first introduced in this manner by Leslie Greengard and Vladimir Rokhlin Jr. and is based on the multipole expansion of the vector Helmholtz equation. By treating the interactions between far-away basis functions using the FMM, the corresponding matrix elements do not need to be explicitly stored, resulting in a significant reduction in required memory. If the FMM is then applied in a hierarchical manner, it can imp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
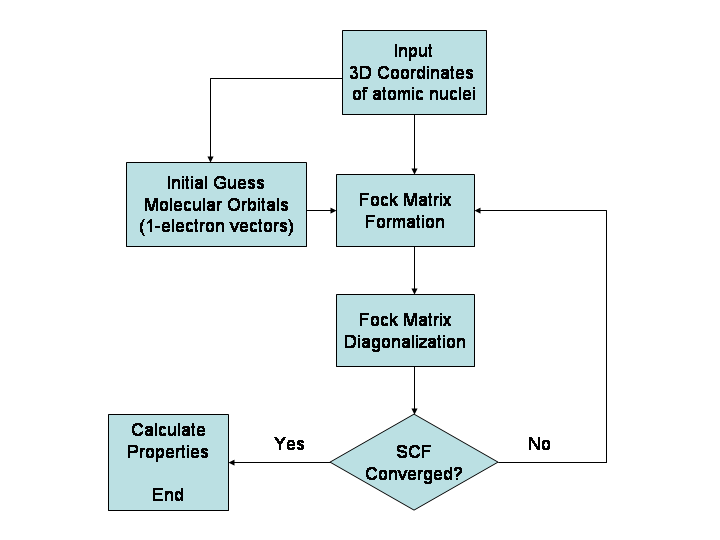
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Message Passing Interface
The Message Passing Interface (MPI) is a portable message-passing standard designed to function on parallel computing architectures. The MPI standard defines the syntax and semantics of library routines that are useful to a wide range of users writing portable message-passing programs in C, C++, and Fortran. There are several open-source MPI implementations, which fostered the development of a parallel software industry, and encouraged development of portable and scalable large-scale parallel applications. History The message passing interface effort began in the summer of 1991 when a small group of researchers started discussions at a mountain retreat in Austria. Out of that discussion came a Workshop on Standards for Message Passing in a Distributed Memory Environment, held on April 29–30, 1992 in Williamsburg, Virginia. Attendees at Williamsburg discussed the basic features essential to a standard message-passing interface and established a working group to continu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
OpenMP
OpenMP is an application programming interface (API) that supports multi-platform shared-memory multiprocessing programming in C, C++, and Fortran, on many platforms, instruction-set architectures and operating systems, including Solaris, AIX, FreeBSD, HP-UX, Linux, macOS, Windows and OpenHarmony. It consists of a set of compiler directives, library routines, and environment variables that influence run-time behavior. OpenMP is managed by the nonprofit technology consortium ''OpenMP Architecture Review Board'' (or ''OpenMP ARB''), jointly defined by a broad swath of leading computer hardware and software vendors, including Arm, AMD, IBM, Intel, Cray, HP, Fujitsu, Nvidia, NEC, Red Hat, Texas Instruments, and Oracle Corporation. OpenMP uses a portable, scalable model that gives programmers a simple and flexible interface for developing parallel applications for platforms ranging from the standard desktop computer to the supercomputer. An application built with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inria
The National Institute for Research in Digital Science and Technology (Inria) () is a French national research institution focusing on computer science and applied mathematics. It was created under the name French Institute for Research in Computer Science and Automation (IRIA) () in 1967 at Rocquencourt near Paris, part of Plan Calcul. Its first site was the historical premises of SHAPE (central command of NATO military forces), which is still used as Inria's main headquarters. In 1980, IRIA became INRIA. Since 2011, it has been styled ''Inria''. Inria is a Public Scientific and Technical Research Establishment (EPST) under the double supervision of the French Ministry of National Education, Advanced Instruction and Research and the Ministry of Economy, Finance and Industry. Administrative status Inria has nine research centers distributed across France (in Bordeaux, Grenoble- Inovallée, Lille, Lyon, Nancy, Paris- Rocquencourt, Rennes, Saclay, and Sophia Antipolis) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-body Simulation
In physics and astronomy, an ''N''-body simulation is a simulation of a dynamical system of particles, usually under the influence of physical forces, such as gravity (see n-body problem, ''n''-body problem for other applications). ''N''-body simulations are widely used tools in astrophysics, from investigating the dynamics of few-body systems like the Earth-Moon-Sun system to understanding the evolution of the large-scale structure of the universe. In physical cosmology, ''N''-body simulations are used to study processes of non-linear structure formation such as galaxy filaments and galaxy halos from the influence of dark matter. Direct ''N''-body simulations are used to study the dynamical evolution of star clusters. Nature of the particles The 'particles' treated by the simulation may or may not correspond to physical objects which are particulate in nature. For example, an N-body simulation of a star cluster might have a particle per star, so each particle has some physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipole Expansion
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Multipole expansions are useful because, similar to Taylor series, oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on \R^3, or less often on \R^n for some other Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space. The multipole expansion is expressed as a sum of terms with progressively finer angular f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barnes–Hut Simulation
The Barnes–Hut simulation (named after Joshua Barnes and Piet Hut) is an approximation algorithm for performing an N-body simulation. It is notable for having Big O notation, order O(''n'' log ''n'') compared to a direct-sum algorithm which would be O(''n''2). The simulation volume is usually divided up into cubic cells via an octree (in a three-dimensional space), so that only Point particle, particles from nearby cells need to be treated individually, and particles in distant cells can be treated as a single large particle centered at the cell's center of mass (or as a low-order multipole expansion). This can dramatically reduce the number of particle pair interactions that must be computed. Some of the most demanding high-performance computing projects perform computational astrophysics using the Barnes–Hut treecode algorithm, such as DEGIMA. Algorithm The Barnes–Hut tree In a three-dimensional n-body simulation, ''N''-body simulation, the Barnes–Hut a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrange Polynomial
In numerical analysis, the Lagrange interpolating polynomial is the unique polynomial of lowest degree that interpolates a given set of data. Given a data set of coordinate pairs (x_j, y_j) with 0 \leq j \leq k, the x_j are called ''nodes'' and the y_j are called ''values''. The Lagrange polynomial L(x) has degree \leq k and assumes each value at the corresponding node, L(x_j) = y_j. Although named after Joseph-Louis Lagrange, who published it in 1795, the method was first discovered in 1779 by Edward Waring. It is also an easy consequence of a formula published in 1783 by Leonhard Euler. Uses of Lagrange polynomials include the Newton–Cotes method of numerical integration, Shamir's secret sharing scheme in cryptography, and Reed–Solomon error correction in coding theory. For equispaced nodes, Lagrange interpolation is susceptible to Runge's phenomenon of large oscillation. Definition Given a set of k + 1 nodes \, which must all be distinct, x_j \neq x_m for ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chebyshev Nodes
In numerical analysis, Chebyshev nodes (also called Chebyshev points or a Chebyshev grid) are a set of specific algebraic numbers used as nodes for polynomial interpolation and numerical integration. They are the Projection (linear algebra), projection of a set of equispaced points on the unit circle onto the real interval [-1, 1], the circle's diameter. There are two kinds of Chebyshev nodes. The ''Chebyshev nodes of the first kind'', also called the Chebyshev–Gauss nodes or Chebyshev zeros, are the Zero of a function, zeros of a Chebyshev polynomial of the first kind, . The corresponding ''Chebyshev nodes of the second kind'', also called the Chebyshev–Lobatto nodes or Chebyshev extrema, are the Maximum and minimum, extrema of , which are also the zeros of a Chebyshev polynomial of the second kind, , along with the two endpoints of the interval. Both types of numbers are commonly referred to as ''Chebyshev nodes'' or ''Chebyshev points'' in literature. They are named aft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |