|
Constant Elasticity Of Variance Model
In mathematical finance, the CEV or constant elasticity of variance model is a stochastic volatility model, although technically it would be classed more precisely as a local volatility model, that attempts to capture stochastic volatility and the leverage effect. The model is widely used by practitioners in the financial industry, especially for modelling equities and commodities. It was developed by John Carrington Cox, John Cox in 1975. Dynamic The CEV model is a stochastic process which evolves according to the following stochastic differential equation: :\mathrmS_t = \mu S_t \mathrmt + \sigma S_t ^ \mathrmW_t in which ''S'' is the spot price, ''t'' is time, and ''μ'' is a parameter characterising the drift, ''σ'' and ''γ'' are volatility parameters, and ''W'' is a Brownian motion. It is a special case of a general local volatility model, written as :\mathrmS_t = \mu S_t \mathrmt + v(t,S_t) S_t \mathrmW_t where the price return volatility is :v(t, S_t)=\sigma S_t^ The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Volatility
A local volatility model, in mathematical finance and financial engineering, is an option pricing model that treats Volatility (finance), volatility as a function of both the current asset level S_t and of time t . As such, it is a generalisation of the Black–Scholes model, where the volatility is a constant (i.e. a trivial function of S_t and t ). Local volatility models are often compared with stochastic volatility, stochastic volatility models, where the instantaneous volatility is not just a function of the asset level S_t but depends also on a new "global" randomness coming from an additional random component. Formulation In mathematical finance, the asset ''S''''t'' that Underlying, underlies a financial derivative is typically assumed to follow a stochastic differential equation of the form : dS_t = (r_t-d_t) S_t\,dt + \sigma_t S_t\,dW_t , under the risk neutral measure, where r_t is the instantaneous risk-free interest rate, risk free rate, giving an average ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Finance
Mathematical finance, also known as quantitative finance and financial mathematics, is a field of applied mathematics, concerned with mathematical modeling in the financial field. In general, there exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other. Mathematical finance overlaps heavily with the fields of computational finance and financial engineering. The latter focuses on applications and modeling, often with the help of stochastic asset models, while the former focuses, in addition to analysis, on building tools of implementation for the models. Also related is quantitative investing, which relies on statistical and numerical models (and lately machine learning) as opposed to traditional fundamental analysis when managing portfolios. French mathematician Louis Bachelier's doctoral thesis, defended in 1900, is considered the first scholarly work on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Louis Bachelier
Louis Jean-Baptiste Alphonse Bachelier (; 11 March 1870 – 28 April 1946) was a French mathematician at the turn of the 20th century. He is credited with being the first person to model the stochastic process now called Brownian motion, as part of his doctoral thesis ''The Theory of Speculation'' (''Théorie de la spéculation'', defended in 1900). Bachelier's doctoral thesis, which introduced the first mathematical model of Brownian motion and its use for valuing stock options, was the first paper to use advanced mathematics in the study of finance. His Bachelier model has been influential in the development of other widely used models, including the Black-Scholes model. Bachelier is considered as the forefather of mathematical finance and a pioneer in the study of stochastic processes. Early years Bachelier was born in Le Havre, in Seine-Maritime. His father was a wine merchant and amateur scientist, and the vice-consul of Venezuela at Le Havre. His mother was the da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Options (finance)
In finance, an option is a contract which conveys to its owner, the ''holder'', the right, but not the obligation, to buy or sell a specific quantity of an underlying asset or instrument at a specified strike price on or before a specified date, depending on the style of the option. Options are typically acquired by purchase, as a form of compensation, or as part of a complex financial transaction. Thus, they are also a form of asset (or contingent liability) and have a valuation that may depend on a complex relationship between underlying asset price, time until expiration, market volatility, the risk-free rate of interest, and the strike price of the option. Options may be traded between private parties in '' over-the-counter'' (OTC) transactions, or they may be exchange-traded in live, public markets in the form of standardized contracts. Definition and application An option is a contract that allows the holder the right to buy or sell an underlying asset or financial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SABR Volatility Model
In mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "stochastic alpha, beta, rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the financial industry, especially in the interest rate derivative markets. It was developed by Patrick S. Hagan, Deep Kumar, Andrew Lesniewski, and Diana Woodward. Dynamics The SABR model describes a single forward F, such as a LIBOR forward rate, a forward swap rate, or a forward stock price. This is one of the standards in market used by market participants to quote volatilities. The volatility of the forward F is described by a parameter \sigma. SABR is a dynamic model in which both F and \sigma are represented by stochastic state variables whose time evolution is given by the following system of stochastic differential equations: :dF_t=\sigma_t \left(F_t\right)^\beta\, dW_t, :d\sigma_t=\a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Volatility
In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others. Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, models based on Black-Scholes assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
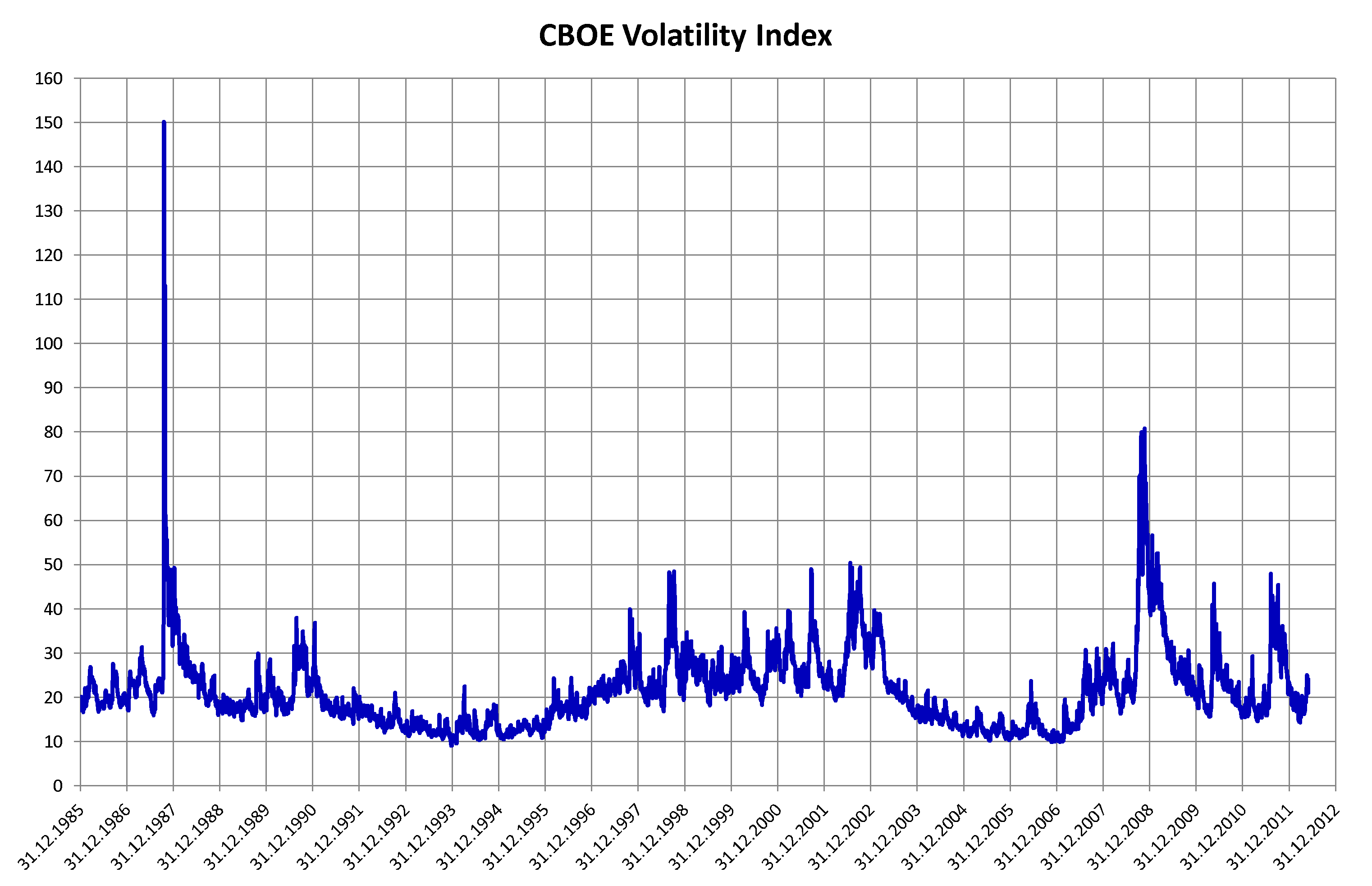
Volatility (finance)
In finance, volatility (usually denoted by "sigma, σ") is the Variability (statistics), degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bachelier Model
The Bachelier model is a model of an asset price under Brownian motion presented by Louis Bachelier on his PhD thesis ''The Theory of Speculation'' (''Théorie de la spéculation'', published 1900). It is also called "Normal Model" equivalently (as opposed to "Log-Normal Model" or "Black-Scholes Model"). One early criticism of the Bachelier model is that the probability distribution which he chose to use to describe stock prices allowed for negative prices. (His doctoral dissertation was graded down because of that feature.) The (much) later Black-Scholes-(Merton) Model addresses that issue by positing stock prices as following a log-normal distribution which does not allow negative values. This in turn, implies that returns follow a normal distribution. On April 8, 2020, the CME Group posted the note ''CME Clearing Plan to Address the Potential of a Negative Underlying in Certain Energy Options Contracts'', saying that after a threshold on price, it would change its standard e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Brownian Motion
A geometric Brownian motion (GBM) (also known as exponential Brownian motion) is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion (also called a Wiener process) with drift. It is an important example of stochastic processes satisfying a stochastic differential equation (SDE); in particular, it is used in mathematical finance to model stock prices in the Black–Scholes model. Technical definition: the SDE A stochastic process ''S''''t'' is said to follow a GBM if it satisfies the following stochastic differential equation (SDE): : dS_t = \mu S_t\,dt + \sigma S_t\,dW_t where W_t is a Wiener process or Brownian motion, and \mu ('the percentage drift') and \sigma ('the percentage volatility') are constants. The former parameter is used to model deterministic trends, while the latter parameter models unpredictable events occurring during the motion. Solving the SDE For an arbitrary initial value '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |