|
Conchospiral
In mathematics, a conchospiral a specific type of space spiral on the surface of a cone (a '' conical spiral''), whose floor projection is a logarithmic spiral. Conchospirals are used in biology for modelling snail shells, and flight paths of insects and in electrical engineering for the construction of antennas. Parameterization In cylindrical coordinates, the conchospiral is described by the parametric equations: :r=\mu^t a :\theta=t :z=\mu^t c. The projection of a conchospiral on the (r,\theta) plane is a logarithmic spiral. The parameter \mu controls the opening angle of the projected spiral, while the parameter c controls the slope of the cone on which the curve lies. History The name "conchospiral" was given to these curves by 19th-century German mineralogist Georg Amadeus Carl Friedrich Naumann, in his study of the shapes of sea shells. Applications The conchospiral has been used in the design for radio antenna In radio-frequency engineering, an antenna (Ameri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Spiral
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects. Two-dimensional A two-dimensional, or plane, spiral may be easily described using polar coordinates, where the radius r is a monotonic continuous function of angle \varphi: * r=r(\varphi)\; . The circle would be regarded as a degenerate case (the function not being strictly monotonic, but rather constant). In ''x-y-coordinates'' the curve has the parametric representation: * x=r(\varphi)\cos\varphi \ ,\qquad y=r(\varphi)\sin\varphi\; . Examples Some of the most important sorts of two-dimensional spirals include: * The Archimedean spiral: r=a \varphi * The hyperbolic spiral: r = a/ \varphi * Fermat's spiral: r= a\varphi^ * The lituus: r = a\varphi^ * The logarithmic spiral: r=ae^ * The Cornu spiral or ''clothoid'' * The Fibonacci spiral and golden spiral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
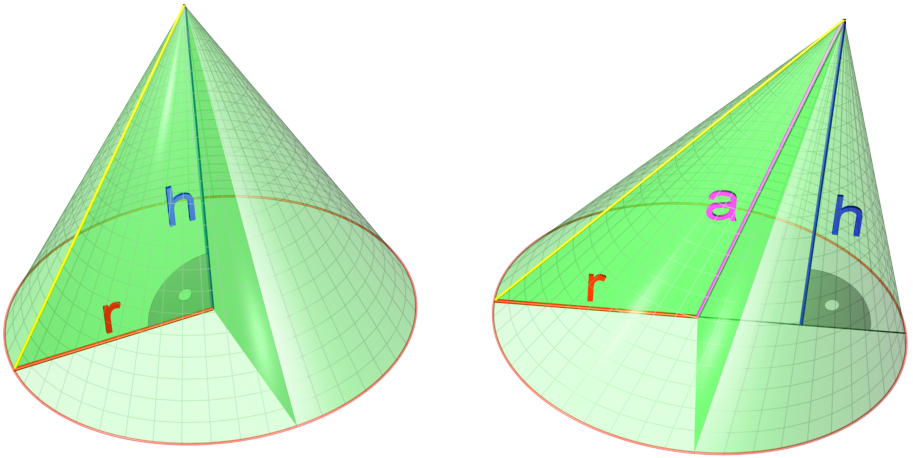
Cone
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Spiral
In mathematics, a conical spiral, also known as a conical helix, is a space curve on a right circular cone, whose floor projection is a plane spiral. If the floor projection is a logarithmic spiral, it is called ''conchospiral'' (from conch). Parametric representation In the x-y-plane a spiral with parametric representation : x=r(\varphi)\cos\varphi \ ,\qquad y=r(\varphi)\sin\varphi a third coordinate z(\varphi) can be added such that the space curve lies on the cone with equation \;m^2(x^2+y^2)=(z-z_0)^2\ ,\ m>0\; : * x=r(\varphi)\cos\varphi \ ,\qquad y=r(\varphi)\sin\varphi\ , \qquad \color \ . Such curves are called conical spirals. They were known to Pappos. Parameter m is the slope of the cone's lines with respect to the x-y-plane. A conical spiral can instead be seen as the orthogonal projection of the floor plan spiral onto the cone. Examples : 1) Starting with an ''archimedean spiral'' \;r(\varphi)=a\varphi\; gives the conical spiral (see diagram) : x=a\va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floor Plan
In architecture and building engineering, a floor plan is a technical drawing to scale, showing a view from above, of the relationships between rooms, spaces, traffic patterns, and other physical features at one level of a structure. Dimensions are usually drawn between the walls to specify room sizes and wall lengths. Floor plans may also include details of fixtures like sinks, water heaters, furnaces, etc. Floor plans may include notes for construction to specify finishes, construction methods, or symbols for electrical items. It is also called a ''plan'' which is a measured plane typically projected at the floor height of , as opposed to an ''elevation'' which is a measured plane projected from the side of a building, along its height, or a section or '' cross section'' where a building is cut along an axis to reveal the interior structure. Overview Similar to a map, the orientation of the view is downward from above, but unlike a conventional map, a plan is drawn at a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similarity, self-similar spiral curve that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer (1525) who called it an "eternal line" ("ewige Linie"). More than a century later, the curve was discussed by René Descartes, Descartes (1638), and later extensively investigated by Jacob Bernoulli, who called it ''Spira mirabilis'', "the marvelous spiral". The logarithmic spiral is distinct from the Archimedean spiral in that the distances between the turnings of a logarithmic spiral increase in a geometric progression, whereas for an Archimedean spiral these distances are constant. Definition In polar coordinates (r, \varphi) the logarithmic spiral can be written as r = ae^,\quad \varphi \in \R, or \varphi = \frac \ln \frac, with e (mathematical constant), e being the base of natural logarithms, and a > 0, k\ne 0 being real constants. In Cartesian coordinates The logarithmi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Snail Shell
The gastropod shell is part of the body of many gastropods, including snails, a kind of mollusc. The shell is an exoskeleton, which protects from predators, mechanical damage, and dehydration, but also serves for muscle attachment and calcium storage. Some gastropods appear shell-less (slugs) but may have a remnant within the mantle, or in some cases the shell is reduced such that the body cannot be retracted within it ( semi-slug). Some snails also possess an operculum that seals the opening of the shell, known as the aperture, which provides further protection. The study of mollusc shells is known as conchology. The biological study of gastropods, and other molluscs in general, is malacology. Shell morphology terms vary by species group. Shell layers The gastropod shell has three major layers secreted by the mantle. The calcareous central layer, ostracum, is typically made of calcium carbonate (CaCO3) precipitated into an organic matrix known as conchiolin. The outermost ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the latter half of the 19th century after the commercialization of the electric telegraph, the telephone, and electrical power generation, distribution, and use. Electrical engineering is divided into a wide range of different fields, including computer engineering, systems engineering, power engineering, telecommunications, radio-frequency engineering, signal processing, instrumentation, photovoltaic cells, electronics, and optics and photonics. Many of these disciplines overlap with other engineering branches, spanning a huge number of specializations including hardware engineering, power electronics, Electromagnetism, electromagnetics and waves, microwave engineering, nanotechnology, electrochemistry, renewable energies, mechatronics/control ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antenna (radio)
In radio-frequency engineering, an antenna (American English) or aerial (British English) is an electronic device that converts an alternating current, alternating electric current into radio waves (transmitting), or radio waves into an electric current (receiving). It is the interface between radio waves Radio propagation, propagating through space and electric currents moving in metal Electrical conductor, conductors, used with a transmitter or receiver (radio), receiver. In transmission (telecommunications), transmission, a radio transmitter supplies an electric current to the antenna's Terminal (electronics), terminals, and the antenna radiates the energy from the current as electromagnetic radiation, electromagnetic waves (radio waves). In receiver (radio), reception, an antenna intercepts some of the power of a radio wave in order to produce an electric current at its terminals, that is applied to a receiver to be amplifier, amplified. Antennas are essential components ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Coordinates
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in a solid ball versus sphere surface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term "cylinder" could refer to either of these or to an even more specialized object, the '' right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George A. Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Georg Amadeus Carl Friedrich Naumann
Georg Amadeus Carl Friedrich Naumann (30 May 1797 – 26 November 1873), also known as Karl Friedrich Naumann, was a German mineralogist and geologist. The crater Naumann on the Moon is named after him. Life Naumann was born at Dresden, the son of a distinguished musician and composer. He received his early education at Pforta, studied at Freiberg under Werner, and afterwards at Leipzig and Jena. He graduated at Jena, and was occupied in 1823 in teaching in that town and in 1824 at Leipzig. In 1826 he succeeded Mohs as professor of crystallography, in 1835 he became professor also of geognosy at Freiberg; and in 1842 he was appointed professor of mineralogy and geognosy in the University of Leipzig. At Freiberg he was charged with the preparation of a geological map of Saxony, which he carried out with the aid of Bernhard von Cotta in 1846. Naumann was a man of encyclopedic knowledge, lucid and fluent as a teacher. Early in life (1821-1822) he traveled in Norway, and his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |