|
Cointegration
In econometrics, cointegration is a statistical property describing a long-term, stable relationship between two or more time series variables, even if those variables themselves are individually non-stationary (i.e., they have trends). This means that despite their individual fluctuations, the variables move together in the long run, anchored by an underlying equilibrium relationship. More formally, if several time series are individually integrated of order ''d'' (meaning they require ''d'' differences to become stationary) but a linear combination of them is integrated of a lower order, then those time series are said to be cointegrated. That is, if (''X'',''Y'',''Z'') are each integrated of order ''d'', and there exist coefficients ''a'',''b'',''c'' such that is integrated of order less than d, then ''X'', ''Y'', and ''Z'' are cointegrated. Cointegration is a crucial concept in time series analysis, particularly when dealing with variables that exhibit trends, such as ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johansen Test
In statistics, the Johansen test, named after Søren Johansen, is a procedure for testing cointegration of several, say ''k'', Order of integration, I(1) time series. This test permits more than one cointegrating relationship so is more generally applicable than the Cointegration#Engle–Granger_two-step_method, Engle-Granger test which is based on the Dickey–Fuller test, Dickey–Fuller (or the Augmented Dickey–Fuller test, augmented) test for unit roots in the residuals from a single (estimated) cointegrating relationship. Types There are two types of Johansen test, either with Trace (linear algebra), trace or with eigenvalue, and the inferences might be a little bit different. The null hypothesis for the trace test is that the number of cointegration vectors is ''r'' = ''r''* < ''k'', vs. the alternative that ''r'' = ''k''. Testing proceeds sequentially for ''r''* = 1,2, etc. and the first non-rejection of the null is taken as an esti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Break
In econometrics and statistics, a structural break is an unexpected change over time in the parameters of regression models, which can lead to huge forecasting errors and unreliability of the model in general. This issue was popularised by David Hendry, who argued that lack of stability of coefficients frequently caused forecast failure, and therefore we must routinely test for structural stability. Structural stability − i.e., the time-invariance of regression coefficients − is a central issue in all applications of linear regression models. Structural break tests A single break in mean with a known breakpoint For linear regression models, the Chow test is often used to test for a single break in mean at a known time period for . This test assesses whether the coefficients in a regression model are the same for periods and . Other forms of structural breaks Other challenges occur where there are: :Case 1: a known number of breaks in mean with unknown break ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clive Granger
Sir Clive William John Granger (; 4 September 1934 – 27 May 2009) was a British econometrician known for his contributions to nonlinear time series analysis. He taught in Britain, at the University of Nottingham and in the United States, at the University of California, San Diego. Granger was awarded the Nobel Memorial Prize in Economic Sciences in 2003 in recognition of the contributions that he and his co-winner, Robert F. Engle, had made to the analysis of time series data. This work fundamentally changed the way in which economists analyse financial and macroeconomic data. Biography Early life Clive Granger was born in 1934 in Swansea, south Wales, United Kingdom, to Edward John Granger and Evelyn Granger. The next year his parents moved to Lincoln. During World War II Granger and his mother moved to Cambridge because Edward joined the Royal Air Force and deployed to North Africa. Here they stayed first with Evelyn's mother, then later Edward's parents, while Clive beg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrics
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics", '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract ( 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spurious Correlation
In statistics, a spurious relationship or spurious correlation is a mathematical relationship in which two or more events or variables are associated but '' not'' causally related, due to either coincidence or the presence of a certain third, unseen factor (referred to as a "common response variable", "confounding factor", or " lurking variable"). Examples An example of a spurious relationship can be found in the time-series literature, where a spurious regression is one that provides misleading statistical evidence of a linear relationship between independent non-stationary variables. In fact, the non-stationarity may be due to the presence of a unit root in both variables. In particular, any two nominal economic variables are likely to be correlated with each other, even when neither has a causal effect on the other, because each equals a real variable times the price level, and the common presence of the price level in the two data series imparts correlation to them. (See ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sam Ouliaris
Sam, SAM or variants may refer to: Places * Sam, Benin * Sam, Boulkiemdé, Burkina Faso * Sam, Bourzanga, Burkina Faso * Sam, Kongoussi, Burkina Faso * Sam, Iran * Sam, Teton County, Idaho, United States, a populated place People and fictional characters * Sam (given name), a list of people and fictional characters with the given name or nickname * Sam (surname), a list of people with the surname ** Cen (surname) (岑), romanized "Sam" in Cantonese ** Shen (surname) (沈), often romanized "Sam" in Cantonese and other languages Religious or legendary figures * Sam (Book of Mormon), elder brother of Nephi * Sām, a Persian mythical folk hero * Sam Ziwa, an uthra (angel or celestial being) in Mandaeism * Sam, Shem in Islam Animals * Sam (army dog) (died 2000) * Sam (horse) (b 1815), British Thoroughbred * Sam (koala) (died 2009), rescued after 2009 bush fires in Victoria, Australia * Sam (orangutan), in the movie ''Dunston Checks In'' * Sam (ugly dog) (1990–2005), voted the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter C
Peter may refer to: People * List of people named Peter, a list of people and fictional characters with the given name * Peter (given name) ** Saint Peter (died 60s), apostle of Jesus, leader of the early Christian Church * Peter (surname), a surname (including a list of people with the name) Culture * Peter (actor) (born 1952), stage name Shinnosuke Ikehata, a Japanese dancer and actor * Peter (1934 film), ''Peter'' (1934 film), a film directed by Henry Koster * Peter (2021 film), ''Peter'' (2021 film), a Marathi language film * Peter (Fringe episode), "Peter" (''Fringe'' episode), an episode of the television series ''Fringe'' * Peter (novel), ''Peter'' (novel), a 1908 book by Francis Hopkinson Smith * Peter (short story), "Peter" (short story), an 1892 short story by Willa Cather * Peter (album), ''Peter'' (album), a 1972 album by Peter Yarrow * ''Peter'', a 1993 EP by Canadian band Eric's Trip * "Peter", 2024 song by Taylor Swift from ''The Tortured Poets Department, The Tort ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phillips–Perron Test
In statistics, the Phillips–Perron test (named after Peter C. B. Phillips and Pierre Perron) is a unit root test. That is, it is used in time series In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. ... analysis to test the null hypothesis that a time series is integrated of order 1. It builds on the Dickey–Fuller test of the null hypothesis \rho = 1 in \Delta y_= (\rho -1)y_+u_\,, where \Delta is the first difference operator. Like the augmented Dickey–Fuller test, the Phillips–Perron test addresses the issue that the process generating data for y_ might have a higher order of autocorrelation than is admitted in the test equation—making y_ endogenous and thus invalidating the Dickey–Fuller t-test. Whilst the augmented Dickey–Fuller test addresses this issue by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Dickey–Fuller Test
In statistics, an augmented Dickey–Fuller test (ADF) tests the null hypothesis that a unit root is present in a time series sample. The alternative hypothesis depends on which version of the test is used, but is usually stationarity or trend-stationarity. It is an augmented version of the Dickey–Fuller test for a larger and more complicated set of time series models. The augmented Dickey–Fuller (ADF) statistic, used in the test, is a negative number. The more negative it is, the stronger the rejection of the hypothesis that there is a unit root at some level of confidence. Testing procedure The procedure for the ADF test is the same as for the Dickey–Fuller test but it is applied to the model :\Delta y_t = \alpha + \beta t + \gamma y_ + \delta_1 \Delta y_ + \cdots + \delta_ \Delta y_ + \varepsilon_t, where \alpha is a constant, \beta the coefficient on a time trend and p the lag order of the autoregressive process. Imposing the constraints \alpha = 0 and \beta = 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spurious Correlation
In statistics, a spurious relationship or spurious correlation is a mathematical relationship in which two or more events or variables are associated but '' not'' causally related, due to either coincidence or the presence of a certain third, unseen factor (referred to as a "common response variable", "confounding factor", or " lurking variable"). Examples An example of a spurious relationship can be found in the time-series literature, where a spurious regression is one that provides misleading statistical evidence of a linear relationship between independent non-stationary variables. In fact, the non-stationarity may be due to the presence of a unit root in both variables. In particular, any two nominal economic variables are likely to be correlated with each other, even when neither has a causal effect on the other, because each equals a real variable times the price level, and the common presence of the price level in the two data series imparts correlation to them. (See ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
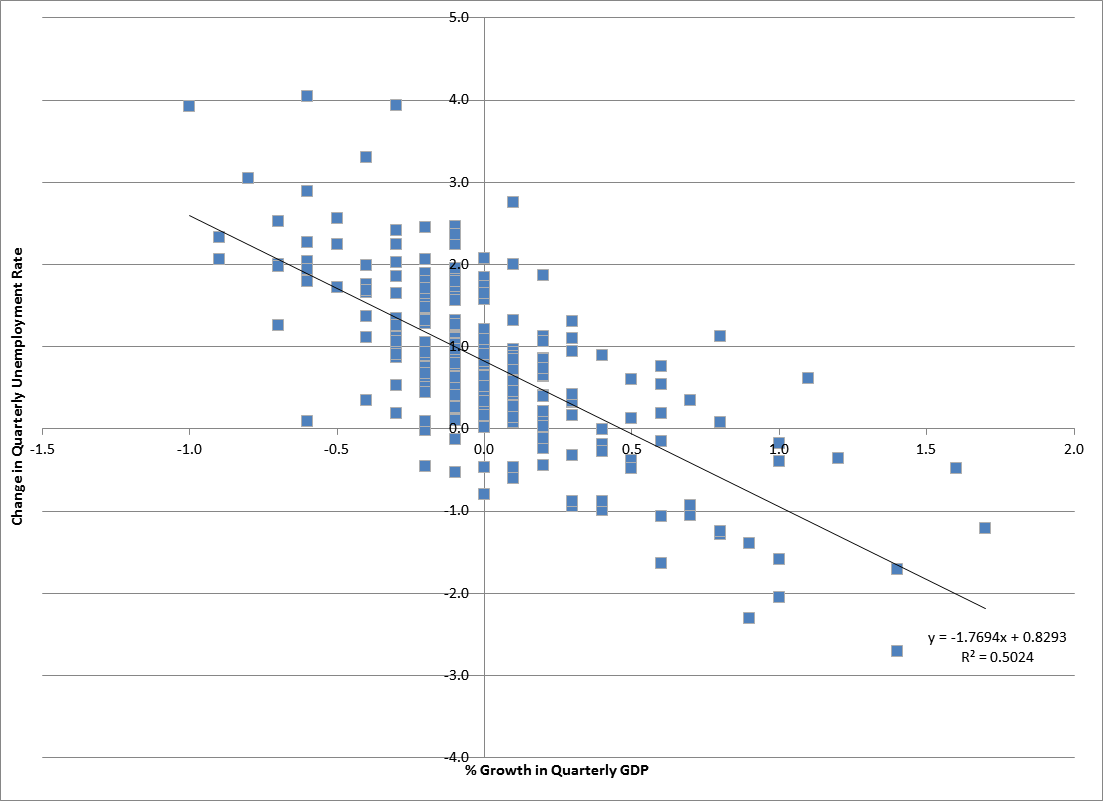
R-squared
In statistics, the coefficient of determination, denoted ''R''2 or ''r''2 and pronounced "R squared", is the proportion of the variation in the dependent variable that is predictable from the independent variable(s). It is a statistic used in the context of statistical models whose main purpose is either the prediction of future outcomes or the testing of hypotheses, on the basis of other related information. It provides a measure of how well observed outcomes are replicated by the model, based on the proportion of total variation of outcomes explained by the model. There are several definitions of ''R''2 that are only sometimes equivalent. In simple linear regression (which includes an intercept), ''r''2 is simply the square of the sample ''correlation coefficient'' (''r''), between the observed outcomes and the observed predictor values. If additional regressors are included, ''R''2 is the square of the '' coefficient of multiple correlation''. In both such cases, the coeffi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ... model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Some sources consider OLS to be linear regression. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |