|
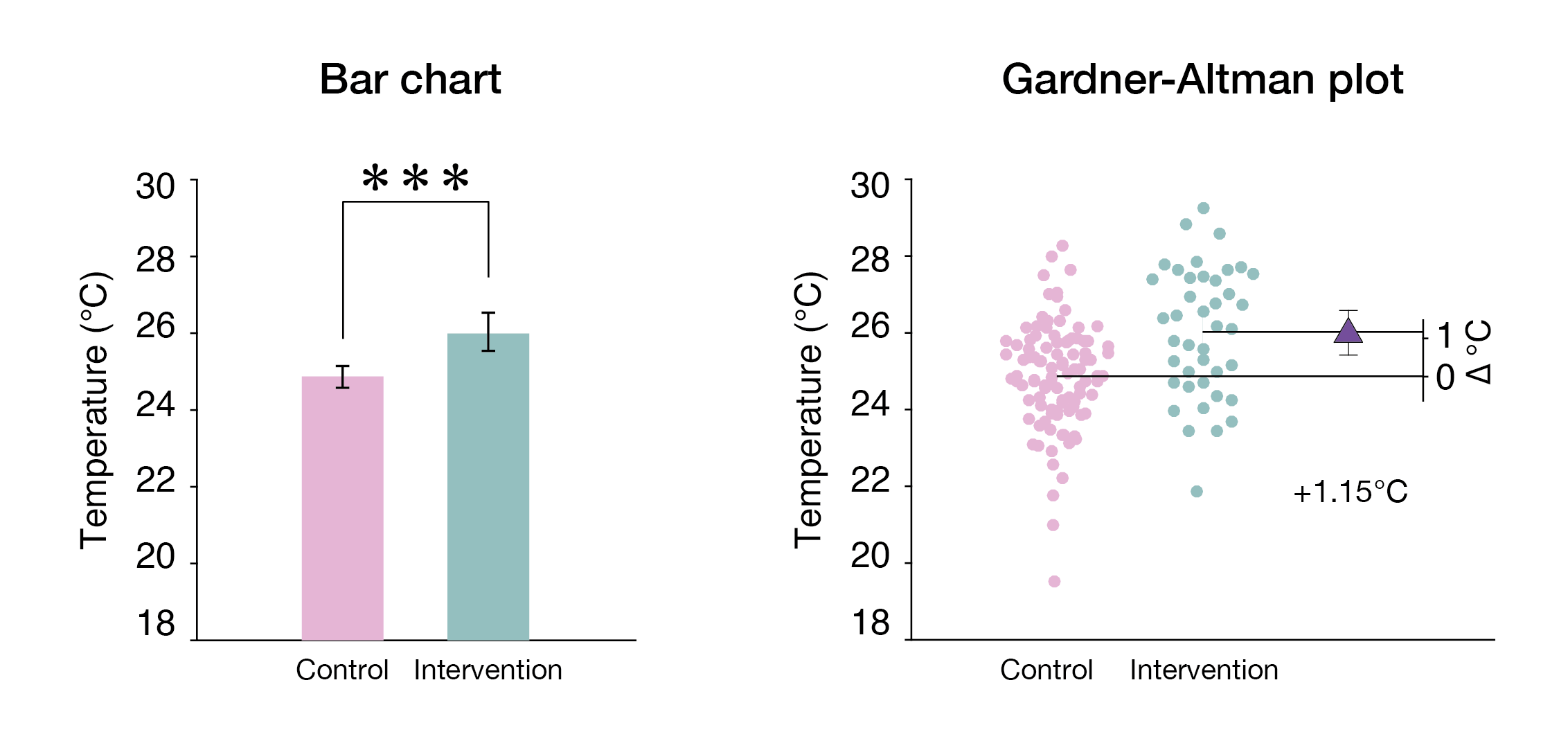
Cohen's D
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event (such as a heart attack) happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics. Effect size is an essential component when evaluating the strength of a statistical claim, and it is the first item (magnitude) in the MAGI ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Estimation Statistics
Estimation statistics, or simply estimation, is a data analysis framework that uses a combination of effect sizes, confidence intervals, precision planning, and meta-analysis to plan experiments, analyze data and interpret results. It complements hypothesis testing approaches such as null hypothesis significance testing (NHST), by going beyond the question is an effect present or not, and provides information about how large an effect is. Estimation statistics is sometimes referred to as ''the new statistics''. The primary aim of estimation methods is to report an effect size (a point estimate) along with its confidence interval, the latter of which is related to the precision of the estimate. The confidence interval summarizes a range of likely values of the underlying population effect. Proponents of estimation see reporting a ''P'' value as an unhelpful distraction from the important business of reporting an effect size with its confidence intervals, and believe that estimat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), and For example, the absolute value of 3 and the absolute value of −3 is The absolute value of a number may be thought of as its distance from zero. Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts. Terminology and notation In 1806, Jean-Robert Argand introduced the term ''module'', meaning ''unit of measure'' in French, specifically for the ''complex'' absolute value, Oxford English Dictionary, Draft Revision, Ju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's ''r'', the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Kar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Explained Variation
In statistics, explained variation measures the proportion to which a mathematical model accounts for the variation ( dispersion) of a given data set. Often, variation is quantified as variance; then, the more specific term explained variance can be used. The complementary part of the total variation is called unexplained or residual variation. Definition in terms of information gain Information gain by better modelling Following Kent (1983), we use the Fraser information (Fraser 1965) :F(\theta) = \int \textrmr\,g(r)\,\ln f(r;\theta) where g(r) is the probability density of a random variable R\,, and f(r;\theta)\, with \theta\in\Theta_i (i=0,1\,) are two families of parametric models. Model family 0 is the simpler one, with a restricted parameter space \Theta_0\subset\Theta_1. Parameters are determined by maximum likelihood estimation, :\theta_i = \operatorname_ F(\theta). The information gain of model 1 over model 0 is written as :\Gamma(\theta_1:\theta_0) = 2 F(\theta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelson's Paradox
Abelson's paradox is an applied statistics paradox identified by Robert P. Abelson. The paradox pertains to a possible paradoxical relationship between the magnitude of the ''r''2 (i.e., coefficient of determination) effect size and its practical meaning. Abelson's example was obtained from the analysis of the ''r''2 of batting average in baseball Baseball is a bat-and-ball sport played between two teams of nine players each, taking turns batting and fielding. The game occurs over the course of several plays, with each play generally beginning when a player on the fielding ... and skill level. Although batting average is considered among the most significant characteristics necessary for success, the effect size was only a tinyRoseman, I. J., & Read, S. J. (2007). "Psychologist at play: Abelson's life and contributions to psychological science." ''Perspectives on Psychological Science'', 2(1), p. 91. 0.003. See also * List of paradoxes References St ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cohen's D
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the value of a parameter for a hypothetical population, or to the equation that operationalizes how statistics or parameters lead to the effect size value. Examples of effect sizes include the correlation between two variables, the regression coefficient in a regression, the mean difference, or the risk of a particular event (such as a heart attack) happening. Effect sizes complement statistical hypothesis testing, and play an important role in power analyses, sample size planning, and in meta-analyses. The cluster of data-analysis methods concerning effect sizes is referred to as estimation statistics. Effect size is an essential component when evaluating the strength of a statistical claim, and it is the first item (magnitude) in the MAGI ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-value
In null-hypothesis significance testing, the ''p''-value is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. A very small ''p''-value means that such an extreme observed outcome would be very unlikely under the null hypothesis. Reporting ''p''-values of statistical tests is common practice in academic publications of many quantitative fields. Since the precise meaning of ''p''-value is hard to grasp, misuse is widespread and has been a major topic in metascience. Basic concepts In statistics, every conjecture concerning the unknown probability distribution of a collection of random variables representing the observed data X in some study is called a ''statistical hypothesis''. If we state one hypothesis only and the aim of the statistical test is to see whether this hypothesis is tenable, but not to investigate other specific hypotheses, then such a test is called a null ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Correlation
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's ''r'', the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Kar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Test Statistic
A test statistic is a statistic (a quantity derived from the sample) used in statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Journal Of General Psychology
''The Journal of General Psychology'' is a quarterly peer-reviewed scientific journal covering experimental psychology. It was established in 1928 and is published by Routledge. The editors-in-chief are Paula Goolkasian ( University of North Carolina, Charlotte) and David Trafimow (New Mexico State University). According to the ''Journal Citation Reports'', the journal has a 2016 5-year impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 0.612. References External links *List of issues on Taylor & Francis Online Experimental psychology journals Quarterly journals Publications established in 1928 Routledge academic journals English-language journals {{Psychology-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptual And Motor Skills
''Perceptual and Motor Skills'' is a bimonthly peer-reviewed academic journal established by Robert B. Ammons and Carol H. Ammons in 1949. The journal covers research on perception or motor skills. The editor-in-chief is J.D. Ball (Eastern Virginia Medical School). The journal was published by Ammons Scientific, but is now published by SAGE Publications. Abstracting and indexing ''Perceptual and Motor Skills'' is abstracted and indexed in the Social Sciences Citation Index and MEDLINE MEDLINE (Medical Literature Analysis and Retrieval System Online, or MEDLARS Online) is a bibliographic database of life sciences and biomedical information. It includes bibliographic information for articles from academic journals covering medic .... In 2017, the journal's impact factor was 0.703. References External links * Bimonthly journals English-language journals Cognitive science journals Publications established in 1949 Perception journals SAGE Publishing academic journal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |