|
Circular Polarisation
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave. In electrodynamics, the strength and direction of an electric field is defined by its electric field vector. In the case of a circularly polarized wave, the tip of the electric field vector, at a given point in space, relates to the phase of the light as it travels through time and space. At any instant of time, the electric field vector of the wave indicates a point on a helix oriented along the direction of propagation. A circularly polarized wave can rotate in one of two possible senses: ''right-handed circular polarization (RHCP)'' in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and ''left-handed circular polarization (LHCP)'' in which the vector r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular
*
{{disambiguation ...
Circular may refer to: * The shape of a circle * ''Circular'' (album), a 2006 album by Spanish singer Vega * Circular letter (other), a document addressed to many destinations ** Government circular, a written statement of government policy **Circulaire * Circular reasoning, a type of logical fallacy * Circular reference *Circular Quay, Australia *Circular Park, Armenia See also * Circular DNA (other) * Circular Line (other) * Circularity (other) Circularity may refer to: *Circular definition *Circular economy *Circular reasoning Circular reasoning (, "circle in proving"; also known as circular logic) is a fallacy, logical fallacy in which the reasoner begins with what they are trying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnitude (vector)
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and zero is only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meanings. It may be a synonym of "seminorm". It can also refer to a norm that can take inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Waveplate
A waveplate or retarder is an optics, optical device that alters the Polarization (waves), polarization state of a light wave travelling through it. Two common types of waveplates are the ''half-wave plate'', which rotates the polarization direction of linear polarization, linearly polarized light, and the ''quarter-wave plate'', which converts between different elliptical polarizations (such as the special case of converting from linearly polarized light to circular polarization, circularly polarized light and vice versa.) Waveplates are constructed out of a birefringence, birefringent material (such as quartz or mica, or even plastic), for which the index of refraction is different for light that is linearly polarized along one or the other of two certain perpendicular crystal axes. The behavior of a waveplate (that is, whether it is a half-wave plate, a quarter-wave plate, etc.) depends on the thickness of the crystal, the wavelength of light, and the variation of the index of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Wave
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic function, periodic wave whose waveform (shape) is the trigonometric function, trigonometric sine, sine function. In mechanics, as a linear motion over time, this is ''simple harmonic motion''; as rotation, it corresponds to ''uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase (waves), phase) are linear combination, linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Displacement (vector)
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position. Displacement is the shift in location when an object in motion changes from one position to another. For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity (a vector), whose magnitude is the average speed (a scalar quantity). Formulation A displacement may be formulated as a '' relative position'' (resulting from the motion), that is, as the final position of a point relative to its initial position . The corresponding displacement vector can be defined as the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase (waves)
In physics and mathematics, the phase (symbol φ or ϕ) of a wave or other periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is expressed in such a scale that it varies by one full turn as the variable t goes through each period (and F(t) goes through each complete cycle). It may be measured in any angular unit such as degrees or radians, thus increasing by 360° or 2\pi as the variable t completes a full period. This convention is especially appropriate for a sinusoidal function, since its value at any argument t then can be expressed as \varphi(t), the sine of the phase, multiplied by some factor (the amplitude of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.) Usually, whole turns are ignored when expressing the phase; so that \varphi(t) is also a periodic function, with the same period as F, that repeatedly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
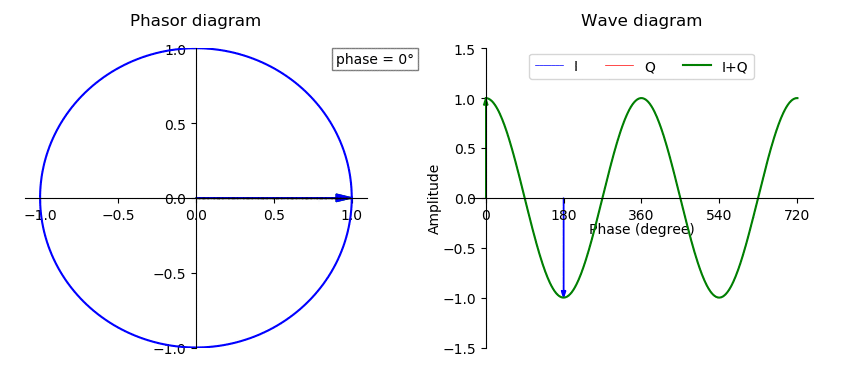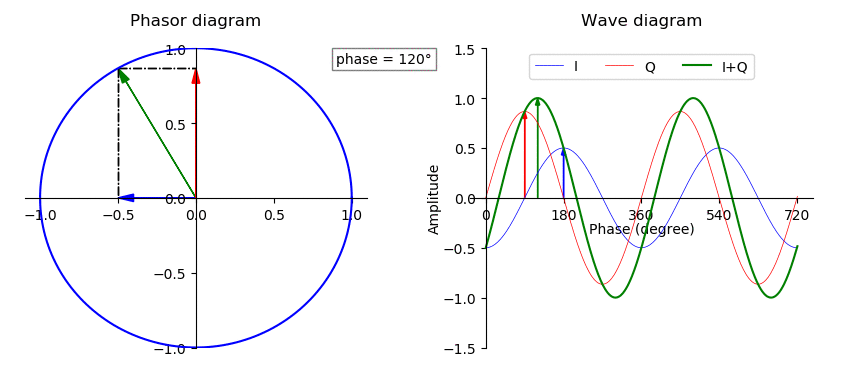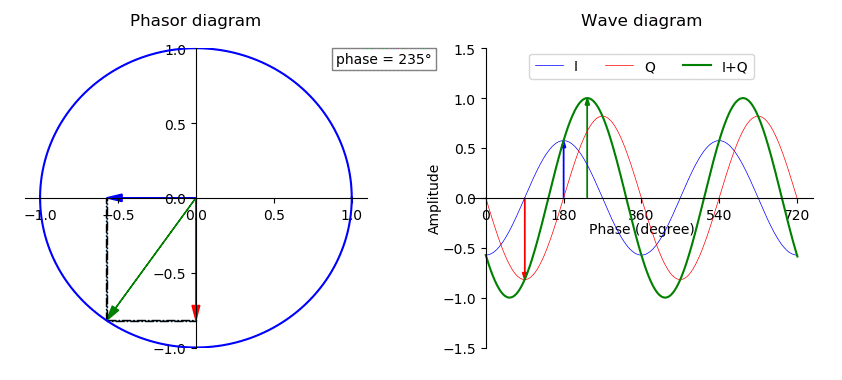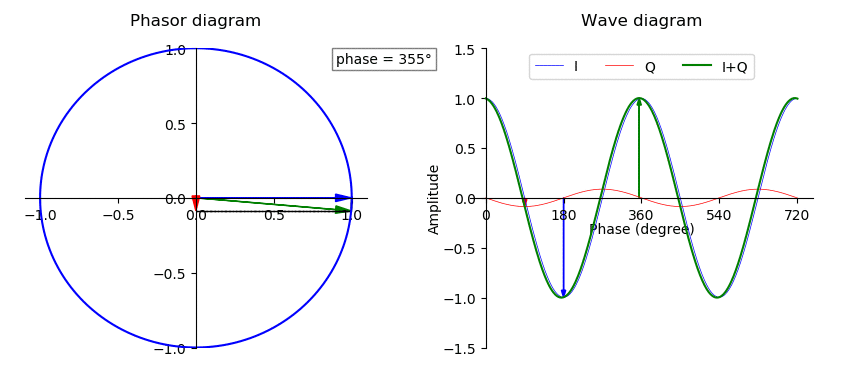
In-phase And Quadrature Components
A sinusoid with modulation can be decomposed into, or synthesized from, two amplitude-modulated sinusoids that are in quadrature phase, i.e., with a phase offset of one-quarter cycle (90 degrees or /2 radians). All three sinusoids have the same center frequency. The two amplitude-modulated sinusoids are known as the in-phase (I) and quadrature (Q) components, which describes their relationships with the amplitude- and phase-modulated carrier. Or in other words, it is possible to create an arbitrarily phase-shifted sine wave, by mixing together two sine waves that are 90° out of phase in different proportions. The implication is that the modulations in some signal can be treated separately from the carrier wave of the signal. This has extensive use in many radio and signal processing applications. I/Q data is used to represent the modulations of some carrier, independent of that carrier's frequency. Orthogonality In vector analysis, a vector with polar coordinates and Car ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats. In other words, it is the distance between consecutive corresponding points of the same ''phase (waves), phase'' on the wave, such as two adjacent crests, troughs, or zero crossings. Wavelength is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The multiplicative inverse, inverse of the wavelength is called the ''spatial frequency''. Wavelength is commonly designated by the Greek letter lambda (''λ''). For a modulated wave, ''wavelength'' may refer to the carrier wavelength of the signal. The term ''wavelength'' may also apply to the repeating envelope (mathematics), envelope of modulated waves or waves formed by Interference (wave propagation), interference of several sinusoids. Assuming a sinusoidal wave moving at a fixed phase velocity, wave speed, wavelength is inversely proportion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality (mathematics)
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called ''coefficient of proportionality'' (or ''proportionality constant'') and its reciprocal is known as ''constant of normalization'' (or ''normalizing constant''). Two sequences are inversely proportional if corresponding elements have a constant product. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely related to ''linearity''. Direct proportionality Given an independent variable ''x'' and a dependent variable ''y'', ''y'' is directly proportional to ''x'' if there is a positive constant ''k'' such that: : y = kx The relation is oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to Euclidean vector, vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Classical Latin, Latin adjective ''rectus'' 'erect, straight, upright, perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to the magnetic field. A permanent magnet's magnetic field pulls on ferromagnetic materials such as iron, and attracts or repels other magnets. In addition, a nonuniform magnetic field exerts minuscule forces on "nonmagnetic" materials by three other magnetic effects: paramagnetism, diamagnetism, and antiferromagnetism, although these forces are usually so small they can only be detected by laboratory equipment. Magnetic fields surround magnetized materials, electric currents, and electric fields varying in time. Since both strength and direction of a magnetic field may vary with location, it is described mathematically by a function (mathematics), function assigning a Euclidean vector, vector to each point of space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Field
An electric field (sometimes called E-field) is a field (physics), physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) describes their capacity to exert attractive or repulsive forces on another charged object. Charged particles exert attractive forces on each other when the sign of their charges are opposite, one being positive while the other is negative, and repel each other when the signs of the charges are the same. Because these forces are exerted mutually, two charges must be present for the forces to take place. These forces are described by Coulomb's law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Informally, the greater the charge of an object, the stronger its electric field. Similarly, an electric field is stronger nearer charged objects and weaker f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |