|
Chu–Harrington Limit
In electrical engineering and telecommunications the Chu–Harrington limit or Chu limit sets a lower limit on the Q factor for a small radio antenna. The theorem was developed in several papers between 1948 and 1960 by Lan Jen Chu, Harold Wheeler, and later by Roger F. Harrington. The definition of a small antenna is one that can fit inside a sphere whose diameter is \tfrac\lambda (radius \tfrac) – a little smaller than wavelength in its widest dimension. For a small antenna the ''Q'' is proportional to the reciprocal of the volume of a sphere that encloses it. In practice this means that there is a limit to the bandwidth of data that can be sent to and received from small antennas such as are used in mobile phones. More specifically, Chu established the limit on ''Q'' for a lossless antenna as Q \geq \frac + \frac for a linear polarized antenna, where a is the radius of the smallest sphere containing the antenna and its current distribution and k = \frac is the waven ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the latter half of the 19th century after the commercialization of the electric telegraph, the telephone, and electrical power generation, distribution, and use. Electrical engineering is divided into a wide range of different fields, including computer engineering, systems engineering, power engineering, telecommunications, radio-frequency engineering, signal processing, instrumentation, photovoltaic cells, electronics, and optics and photonics. Many of these disciplines overlap with other engineering branches, spanning a huge number of specializations including hardware engineering, power electronics, Electromagnetism, electromagnetics and waves, microwave engineering, nanotechnology, electrochemistry, renewable energies, mechatronics/control ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Field
An electromagnetic field (also EM field) is a physical field, varying in space and time, that represents the electric and magnetic influences generated by and acting upon electric charges. The field at any point in space and time can be regarded as a combination of an electric field and a magnetic field. Because of the interrelationship between the fields, a disturbance in the electric field can create a disturbance in the magnetic field which in turn affects the electric field, leading to an oscillation that propagates through space, known as an ''electromagnetic wave''. The way in which charges and currents (i.e. streams of charges) interact with the electromagnetic field is described by Maxwell's equations and the Lorentz force law. Maxwell's equations detail how the electric field converges towards or diverges away from electric charges, how the magnetic field curls around electrical currents, and how changes in the electric and magnetic fields influence each other. The Lor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal Antenna
A fractal antenna is an antenna that uses a fractal, self-similar design to maximize the effective length, or increase the perimeter (on inside sections or the outer structure), of material that can receive or transmit electromagnetic radiation within a given total surface area or volume. Such fractal antennas are also referred to as multilevel and space filling curves, but the key aspect lies in their repetition of a motif over two or more scale sizes,Nathan Cohen (2002) "Fractal antennas and fractal resonators" or "iterations". For this reason, fractal antennas are very compact, multiband or wideband, and have useful applications in cellular telephone and microwave communications. A fractal antenna's response differs markedly from traditional antenna designs, in that it is capable of operating with good-to-excellent performance at many different frequencies simultaneously. Normally, standard antennas have to be "cut" for the frequency for which they are to be used—and thus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capacitor
In electrical engineering, a capacitor is a device that stores electrical energy by accumulating electric charges on two closely spaced surfaces that are insulated from each other. The capacitor was originally known as the condenser, a term still encountered in a few compound names, such as the '' condenser microphone''. It is a passive electronic component with two terminals. The utility of a capacitor depends on its capacitance. While some capacitance exists between any two electrical conductors in proximity in a circuit, a capacitor is a component designed specifically to add capacitance to some part of the circuit. The physical form and construction of practical capacitors vary widely and many types of capacitor are in common use. Most capacitors contain at least two electrical conductors, often in the form of metallic plates or surfaces separated by a dielectric medium. A conductor may be a foil, thin film, sintered bead of metal, or an electrolyte. The nonconductin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inductor
An inductor, also called a coil, choke, or reactor, is a Passivity (engineering), passive two-terminal electronic component, electrical component that stores energy in a magnetic field when an electric current flows through it. An inductor typically consists of an insulated wire wound into a Electromagnetic coil, coil. When the current flowing through the coil changes, the time-varying magnetic field induces an electromotive force (''emf'') (voltage) in the conductor, described by Faraday's law of induction. According to Lenz's law, the induced voltage has a polarity (direction) which opposes the change in current that created it. As a result, inductors oppose any changes in current through them. An inductor is characterized by its inductance, which is the ratio of the voltage to the rate of change of current. In the International System of Units (SI), the unit of inductance is the Henry (unit), henry (H) named for 19th century American scientist Joseph Henry. In the measurement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ladder Line
Twin lead cable is a two-conductor flat cable used as a balanced transmission line to carry radio frequency (RF) signals. It is constructed of two, stranded copper wires, or solid copper-clad steel wires. The wires are held a fixed distance apart by a plastic ribbon that is a good insulator at radio frequencies (usually polyethylene). It is also called (two wire) ribbon cable. The uniform spacing of the wires is the key to the cable's function as a transmission line: Any abrupt change in spacing would cause some of the signal to reflect back toward the source, rather than passing through. The plastic also covers and insulates the wires. The name twin lead is most often used to refer specifically to 300 Ω (Ohm) ribbon cable, the most common type, but on occasion, ''twin lead'' is used to refer to any type of parallel wire line. Parallel wire line is available with several different values of characteristic impedance such as ''twin lead ribbon cable'' (300 Ω), ''win ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hankel Function
Hermann Hankel (14 February 1839 – 29 August 1873) was a German mathematician. Having worked on mathematical analysis during his career, he is best known for introducing the Hankel transform and the Hankel matrix. Biography Hankel was born on 14 February 1839 in Halle, Germany. His father, Wilhelm Gottlieb Hankel, was a physicist. Hankel studied at Nicolai Gymnasium in Leipzig before entering Leipzig University in 1857, where he studied with Moritz Drobisch, August Ferdinand Möbius and his father. In 1860, he started studying at University of Göttingen, where he acquired an interest in function theory under the tutelage of Bernhard Riemann. Following the publication of an award winning article, he proceeded to study under Karl Weierstrass and Leopold Kronecker in Berlin. He received his doctorate in 1862 at Leipzig University. Receiving his teaching qualifications a year after, he was promoted to an associate professor at Leipzig University in 1867. At the same year, he rece ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Bessel Function
Bessel functions, named after Friedrich Bessel who was the first to systematically study them in 1824, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, which represents the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when solving the Helmholtz equation in spherical coordinates. Applications Bessel's equation arises when finding separable s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Function
In physical science and mathematics, the Legendre functions , and associated Legendre functions , , and Legendre functions of the second kind, , are all solutions of Legendre's differential equation. The Legendre polynomials and the associated Legendre polynomials are also solutions of the differential equation in special cases, which, by virtue of being polynomials, have a large number of additional properties, mathematical structure, and applications. For these polynomial solutions, see the separate Wikipedia articles. Legendre's differential equation The general Legendre equation reads \left(1 - x^2\right) y'' - 2xy' + \left[\lambda(\lambda+1) - \frac\right] y = 0, where the numbers and may be complex, and are called the degree and order of the relevant function, respectively. The polynomial solutions when is an integer (denoted ), and are the Legendre polynomials ; and when is an integer (denoted ), and is also an integer with are the associated Legendre polynomi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Harmonic
In mathematics and Outline of physical science, physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics. Since the spherical harmonics form a complete set of orthogonal functions and thus an orthonormal basis, every function defined on the surface of a sphere can be written as a sum of these spherical harmonics. This is similar to periodic functions defined on a circle that can be expressed as a sum of Trigonometric functions, circular functions (sines and cosines) via Fourier series. Like the sines and cosines in Fourier series, the spherical harmonics may be organized by (spatial) angular frequency, as seen in the rows of functions in the illustration on the right. Further, spherical harmonics are basis functions for irreducible representations of Rotation group SO(3), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
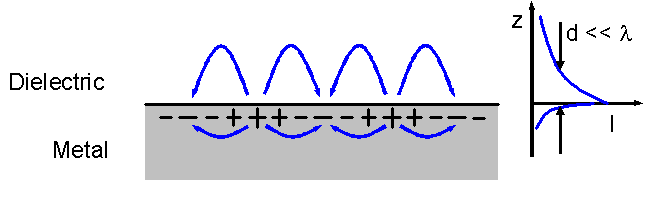
Evanescent Mode
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source (oscillating charges and currents). Even when there is a propagating electromagnetic wave produced (e.g., by a transmitting antenna), one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths (such as the far field of a transmitting antenna). A hallmark of an evanescent field is that there is no net energy flow in that region. Since the net flow of electromagnetic energy is given by the average Poynting vector, this means that the Poynting vector in these regions, as averaged over a complete oscillation cycle, is zero. Use of the term In many cases one cannot simply say that a field is or is not "evanescent" – havin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of reciprocal length, expressed in SI units of cycles per metre or reciprocal metre (m−1). Angular wavenumber, defined as the wave phase divided by time, is a quantity with dimension of angle per length and SI units of radians per metre. They are analogous to temporal frequency, respectively the '' ordinary frequency'', defined as the number of wave cycles divided by time (in cycles per second or reciprocal seconds), and the ''angular frequency'', defined as the phase angle divided by time (in radians per second). In multidimensional systems, the wavenumber is the magnitude of the '' wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |